Slides Flashcards
Goal of The class
Gain a fundamental understanding of the structure-composition-property relationship
Types of properties
There are mechanical, electrical, thermal, and optical properties
Mechanical properties
Materials are brittle, ductile, rubbery, or hard
Brittle materials
This includes things like glass that shatter under stress
ductile materials
These are materials that are able to be bent due to dislocations in their atomic lattice. They do not return to their original shape after being bent though.
Rubbery materials
These are materials that elastically deform usually because of long chained polymers that enable these materials to deform and restructure. Polymers have the quality of rectation to act elastically
Hard materials
These are microcrystalline or nanocrystalline materials that are significant because they diffuse crack propagation very rapidly by minimizing intragranular cracking. This is commonly glass-ceramic materials.
Electrical material types
Materials are either conductors, insulators, or semiconductors
Conductive materials
This is a property of materials with loose electrons in the conductance band. They are able to transfer electrons between atoms.
Defects and impurities within the conductor scatters electrons and lower the conductivity of the material. 2D materials and crystals do not have as much deviation in preferred directions of electron transfer which makes them very good conductors.
Electron scattering length
This is a measure of the mobility of electrons in a material. Generally pure and crystalline materials (for semiconductors) have a longer scattering length which correlates to a higher conductivity.
Units are in cm2V-1s-s
Insulators
These are materials with tightly bound electrons and resist current
Semiconductors
These are materials that can elevate electrons into the conductance band under the right conditions of heat or voltage but below this critical value they act as insulators.
Optical properties
Materials are either opaque (absorbs incident light), transparent (one crystal that does not resonate with the oscillations of light or complete disorder), colored (alters the E of light), or translucent
Scattering in a material
Polycrystalline materials cause scattering as the light ray is reflected at each interface which can make them opaque or translucent
Why is glass clear
There are no reflective surfaces on the interior and the resonant frequencies of amorphous SiO2 are above and below most light. Glass is colored by metals that are able to elevate electrons with the general light wavelengths.
Thermal Properties
Materials are either conductors or insulators (dissipate phonons)
Thermal conductivity
Thermal conductivity is given by K = KL + KE
A high K means that heat is well transferred through the material.
KL is the lattice thermal conductivity (phonons) a low value indicates the material scatters phonons (scatter length =nm)
KE is the electronic thermal conductivity (ability to vibrate) a low value would indicate that electrons can flow without causing much oscillations.
A smaller crystal size enables the flow of electrons but the scattering of photons.
Phonons
These are collective vibrations of atoms along a crystalline arrangement. They have wave-particle duality having a frequency of oscillation and speed of propagation but have quantized vibrational mechanical energy and can be scattered. They transfer heat along a crystalline arrangement.
Number of oscillation modes in N atoms
There are 3N phonon modes in a crystal of N atoms based on Einstein’s model
Types of Phonons
There are optical and acoustic phonons
optical phonons move out of phase in opposite directions (like EMR) They are excited by EMR and create heat by coupling with absorbed EMR
Acoustic Phonons: the neighboring atoms move in the same direction as their neighbors (like sound waves)
Phonon Displacement types
Longitudinal displacement is when phonons move parallel to the direction of propagation
Transverse Displacement is when the phonons move in a direction perpendicular to the direction of propagation
Longitudinal Optical Phonon (LO) motion
If there is a row of phonons numerically labelled 1-n then the odd numbered phonons would move to the left when the even photons move to the right and vice versa
In comparison a longitudinal acoustic phonon would have a whole section of the lattice compress as the other section elongates/dilates
Transverse Acoustic Phonon (TA)
Within this mode of oscilation there is wave propogation out of plane (lateral motion) but it is continuous where neighbors have have simlar oscilation paths
Compared to transverse optical phonons (TO) is when neighboring atoms move in transverse directions but when one atom moves down the other moves up and vice versa.
Distinguishing Phonons
Within a crystal lattice there are 3N modes of osculation which are dependent upon the direction of 3-space being considered. Thus, in simple distinguishing you can look down a certain direction of the lattice to identify the mode of oscillation in that given direction.
allotropism
This is a term that defines different structures of the same composition but can only be applied to materials of pure elemental compositions
Thermal: Diamond vs. graphite
Diamond: The very strong, continuous, and rigid lattice network leads to low phonon scattering therefore very high k (~1000 W/mK)
Graphite: Parallel to plane k ~1950 W/mK this is because in plane the bonds are very strong and the hexagons distribute the vibrations well longitudinally
Perpendicular to plane low k (~5.7 W/mK) this is because the van der waals forces do not tightly oscillate along this dimension
Mechanical: Diamond vs graphite
Diamond is the hardest known material with a moh’s hardness of 10 which is why it can be used as an indenter in mechanical tests
Graphite is very rigid within layer but very weak between layers. This is exploited in it being used as a dry lubricant.
Electrical: Diamond vs. Graphite
Diamond has a wide band gap (5.5 eV) which makes it a very poor conductor (σ = 10-16)
Graphite has pi bonds transverse to the hexagonal layers which makes it incredibly conductive (normal to the plane σ = 10 parallel σ = 105)
Optical: Diamond and Graphite
Diamond has a large band gap (5.5 eV) this means that it is transparent until very low wavelengths near UV/ This is the amount of energy needed to cause the “jump” of electrons. Because of the rigidity of the structure IR does not wiggle the carbon atoms either. Also because diamond is isotropic and homogenous there are not any dipoles for incident EMR to couple with.
Graphite has semi-metal conductance bands which leads to free electrons. This means that it is opaque but also shiny.
Pi bonds
Pi bonds are double bonds that align above and below the planes. In graphite they are delocalized which creates a conductance level.
band gap
If Maxwell’s equation is solved for the electron position the electron’s energy can be found as a function of the direction (wavevector). The band gap is the difference in energy between the conductance band and valency bands.
Photon energy (eV’s)
1 photon usuall equates to ~2-3 eV
band gap diagram
This is a chart that is found by solving the wave function for the electrons position in one direction. These directions are then plugged into KE to plot the energy curves of electrons by direction. The upper lines show electrons in the conduction band (exited and transferrable) and the lower lines show electrons in the valence band (shielded)
The area between the two curves is the band gap and is an area of energy that electrons will never enter in terms of energy. The elevate electrons they must receive enough kinetic energy to jump the band gap.
Types of Probing Energies
There is light (IR-Vis-UV), x-rays, electrons and ion
Charge of probing energies
light: 0
x-rays: 0
Electrons: 1.602*10-19 C
Ions: +
Mass of Probing energies
light: 0
x-rays: 0
Electrons: 9.1*10-31 kg
Ions: Varies 6.6*10-26 Ar; 12*10-26 Ga
Energy of Probes
light: .1-6 eV
x-rays: ~10,000 eV
Electrons: 1-50 keV
Ions: 1-50 keV
Wavelength of Probes
light: 12-.2 μm
x-rays: 1-2 angstroms (.1-.2 nm)
electrons: λ = h/(2mE).5 = ~10pm for E~10 keV
Ions: λ = h/(2mE).5 = .1fm for E~10keV
(2mE).5 for electrons and ions is their momentum respectiely
Momentum of Probes and which have the most/least momentum
Light: p=h/λ
This has the least momentum because it has the longest wavelength. Green light has a momentum of 1.3 * 10-27 kg*m/s
x-rays: p=h/λ ~10-27
Electrons: p=[2mE].5 ~10-22
Ions: p=[2mE].5
These have the greatest momentum because they are the most massive and energetic. They have a momentum of 4.4*10-20 kg*m/s
Why to measure the momentum of electrons via energy?
Energy of electrons/ions is easier to determine that their explicit velocities because the kinetic energy can be determined through the process of accelerating the particle in a voltage potential. This also holds true for ions
Focii of Probes
Light: lenses
x-rays: mirrors
Electrons: magnets
Ions: magnets
Determining E for an ion/electron
E = charge*ΔV
Where charge is in coloumbs for the particle (1.602*10-19 C/charge)
ΔV = potential across the gap used to accelerate the charged particle.
eV to J conversion
E = q*V and 1 eV is the energy required by an electron in a electric potential of 1 V
hence, E = qV = 1.6*10-19 * 1
1 eV = 1.6 * 10-19 J
Energy (eV) of a photon at a wavelength in nm
E (eV) = 1242/λ (nm)
Concept of probing
The idea of probing is to cause a destabilization of the material in order to gain information about the material. You increase the entropy (hopefully temporarily) to receive information
What can we probe?
We can probe:
Electronic levels, vibrational levels, rotational levels, and translational energy levels. This fundamentally provides four constraints on our system to derive information
Energy Quantization
This is the idea that when we are probing things we are almost exclusively examining quantized energy levels derived from examining the wavefunction of the thing
When does quantization occur
Whenever a wave is confined (standing wave) the oscillation modes are discretized and can be derived using the schrodinger equation
electronic energy levels change
ΔE ~ 5*10-18 J This is the largest change in energy by level of the differing methods of probing
Vibrational energy level size
ΔE ~ 5*10-20 J
This is the second largest energy level change
Rotational Energy level change
ΔE ~ 5*10-22 J
This is the second smallest change by energy level but it doesn’t really matter because rotation does not readily occur in solids which is our main focus.
Translational change in energy
ΔE ~ 5*10-60 J These are so small that they are often considered to be continuous
ΔE hierarchy for probing (Least to greatest)
Translational Energy, rotational, vibrational, electronic
Bohr Model: Energy of an Electron
En = -13.6 Z2/n2 (eV)
where Z = atomic number and n = energy level
Electron E quantization: why?
If you find the wavefunction representing a certain set of orbitals there will be zero points where P(electron) = 0. These act as control points where oscillations cannot occur and we can consider them to be standing waves.
Energy of vibrations
Atomic oscillators can be described using a wavefunction that resembles a spring or a pendulum where their point where V=0 are control points for the standing wave.
Ev = (v+.5)(h/2pi)[k/m*].5
where: v = vibrational quantum number
k = “spring constant” related to the bonding energy = restoring force constant
m*= reduced mass = (1/m1) + (1/m2) where m1 and m2 are from the oscilating atoms or particles
Rotational Energy
The rotation of a periodically rotating molecule is confined by the moment I of the molecule.
Erot = J(J+1) ℏ2/2I
where J = rotational quantum number
ℏ = h/2pi
I = moment of inertia of the rotating particle
ℏ = ?
ℏ = h/2pi = reduced Planck’s constant
Translational Energy
En = (h2/8mL2)n2
n>0
L = Boundary x
m = mass
Particle in a box
This is a concept that is used to derive the translational energy levels of a particle. It postulates that if we have a particle that can move from 0 to L along x that is confined by a box that there are defined energies of the particle defined by different oscillation modes
Maxwell’s equation for E
E(x,t) = Asin(kx-ωt)
where: k2 = wave number = (ω/c)2
ω = angular frequency = 2pi c/λ
Schrodinger’s time independent function
This is the part of the equation with eiωt
ℏ2/2m + d2 ψ(x)/dx2 =Eψ(x)
How do we derive translational energy?
With schrodingers equation we can guess Asinkx + Bcossinkx where we are limited by ∫01 ψ(x)2 dx =1 and ψ(0)=0 ; ψ(L)=0
We can then solve for the unknowns and plug into schrodingers equation.
Solving for E we get that E= (ℏk)2/2m and k = wavenumber so k*L=npi because the wave must be equal to zero at x=L which only occurs in intervals of pi
Plug k in terms of npi/L and that is the energy equation
UPS
UV photoelectron Spectroscopy
UV light to KE of e
A beam of UV light extracts electrons from samples. The KE is measured to provide information on the binding energy in the valence region that the electron once occupied. It is measured by count/binding energy (eV)
FTIR
Fourier Transform InfraRed
IR to IR
incident IR light is absorbed by vibrational levels. The IR not absorbed is transmitted. Transmittance vs. wavenumber is characteristic of certain materials.
XRF
X-Ray Fluorescence
x-ray to x-ray
X-rays eject core electrons and when the outer ring electrons lower their energy level they emit characteristic x-rays. This is measured in counts/energy. Every atom has many responses that help to constrain the system or make it more complicated.
XPS/ESCA
X-Ray Photoelectron Spectroscopy/ Electron Spectroscopy for Chemical analysis
x-ray to KE of e
Beam of x-rays extracts e from samples the KE is proportional to the binding energies and intensity vs. eV reveals binding energies within certain orbitals
EDS
Energy Dispersive Spectroscopy
electrons to x-rays
Bean of electrons ejects core electrons and when outer electrons relax into vacancy they release characteristic x-rays and we measure count/energy
AES
Auger electron spectroscopy
electron to KE of e
A beam of electrons ejects core electron. An outer electron fills the vacancy and releases energy which ejects another outer electron. This electron is analyzed for KE
RBS
Rutherford Backscattering spectroscopy
ions to KE of ions
Ion beam collides with a sample. E of backscattered ions is measured and the change in energy of the ions is characteristic of atoms in the sample. This is given in energy vs count
SIMS
Secondary Ions Mass Spectroscopy
Ions to charge and mass of ions
Ion beam breaks a sample into ionic fragments. The mass and charge of fragments are measured by MS. Results are MS results; m/z vs intensity
Types of Imaging Techniques
SEM, TEM, AFM
SEM
Scanning Electron Microscopy
Electron source
Backscattered e from scanning beam are collected to image the surface topology and compositional variations
TEM
Transmission Electron Microscopy
Electron source
Electrons are transmitted through a thin sample to produce an image. This is also a diffraction technique that can indicate crystallograhy
AFM
Atomic Force Microscopy
This uses an atomically sharp tip to raster scan a material and produce its topology
Diffraction Techniques
TEM, XRD, ND
ND
Nuetron Diffraction
Neutron Source
Neutron beam diffracted through a sample and generates a diffraction pattern characteristic of crystallagrophy
XRD
X-Ray Diffraction
X-Ray beam is diffracted off of the sample surface to generate a diffraction pattern characteristic of crystallography
What does infrared light represent
This is the radiation of heat. All things radiating heat radiate IR.
Microwave radiation: oscillations
This is the effect of the electric fields of EMR being long enough to couple with molecules to cause oscillations. By coincidence microwaves can couple with water easily to create oscillations. These induce heat and are used to warm things via a microwave oven.
How is frequency related to light energy
An increase in frequency is equivalent to more oscilations/time which is related to increased energy within the wave.
How do x-rays interact with matter
x-rays have significant energy and can couple with larger atoms like calcium and phosphorous in our bones. This is why x-rays show our bones because they are the parts of us that absorb the rays. Smaller atoms (C, O, N) do not couple.
light properties as a wave
As a wave light has wavelength, amplitude, velocity, and time dependent vector quantity (phase dependent).
Amplitude is proportional to intensity
phase can be measured through interference
velocity is proportional to density and crystallographic interactions
and wavelength is proportional to the induced oscillations
Light as a particle
Planck postulated that light as a particle is the photon which are “energy packets” with E = hν
Under this impression light has a momentum given by h/λ and transfers energy through collisions with materials
Force on a charge in a field
F = q X E where q = 1.69 * 10-19 (C) for an electron
Polarization
This is the measure of how distorted the electron field becomes when interacting with an external electric field.
P = εo Χ E
Χ = dielectric susceptibility = f(material) = how electrons do not transfer but shift relative position
εo = permittivity of a vacuum = C1
What is the dielectric susceptibility a function of?
Χ is a material property that varies with the magnitude of a dipole (either induced or natural) and the wavelength of the electric field
Dipole Moment
μ = q X d where d and μ are vectors and points in the direction of the negative charge. Thus μ is in the direction opposite to E.
Charge sign within an E field
An electric field attracts a positive charge.
Three kinds of electric field-matter interactions
- Reorientation: This is the slowest oscillations of materials that is common within radio and microwaves.
- vibrations: These are between pairs of charged atoms and induce phonons in the IR and micro area
- electronic oscillations (Lorentz oscillators): This is the idea of electrons being semi-bound to the nucleas and influenced by high frequency oscillations in the vis or UV range.
Resonant frequency of vibrational oscillators
νo = (1/2pi) (k*μ).5 where k = “spring constant” = f(bonding)
μ = reduced mass = (1/m1+1/m2)
This is used to describe ionic and some covalent bonds that have rather rigid bonds
What determines coupling of vibrational oscillators
A larger mass of the atoms translates to greater time needed to change acceleration. Additionally, a higher spring constant (bond strength) means a higher resonant frequency because there is a greater restoring force.
Resonant frequency of electronic oscillators
ωo is proportional to μ.5 where μ = 1/me because m/n is much larger than the mass of an electron it is the dominant part of the atom that is being polarized by an interactiving light wave.
Is polarization a vector?
P can be described in 3 space by the dielectric susceptibility in each direction. If a material is isotropic or a glass then there is little to no difference between the x, y, and z directions.
P is a function of the wavelength of the light and can interact with multiple E-fields at one point in space/time.
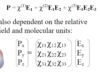
Potential results of light proceeding into a solid
Transmission
Reflection: any change in refractive index causes some light to not enter the material.
absorption: dissipation and coupling which transfers energy to the material
scattering: The change of light direction. There is not energy transfer only energy redirection.
Reflection
R = Ir/Io = (n-1/n+1)2 when the material is transparent and the light incidence is normal to the surface.
This means that with an increase in n there is an increase in R
n proportional to e
the magnitude of n is defined by how strongly electrons couple with the incident light aka the polarizability of the material
n = [1-P/εoE].5 = (εr).5= 1- χ
Three ways to measure the coupling capacity of materials
P, χ, ε, and n are all related and can indicate how strongly light and matter couple. Generally large atoms that have a less dense electronic cloud are more polarizable, have a higher chi, P, epsilon, and n
What material character does n not determine
n cannot give indication to some structural features. For example a single quartz crystal and glass will have the same n. Diffraction bust be used to determine crystallography.
Scattering
this is the phenomenon where light is redirected but energy is not transferred. It occurs when light couples with the natural frequency of electrons and then is remitted radially. It is generally inefficient has a small influence on our observed optical phenomena.
Is = Io (a/λ4) This says that light scattering efficiency is very sensitive to changes in wavelength.
Why is the sky blue?
Scattering efficiency is a function of wavelength and blue light has a lower wavelength than red light meaning that it is more likely to be scattered. Because scattering is a redirection of light path, this means that the blue light is scattered down where we see it. This is why sunsets are red too because the blue light has been scattered since we are directly looking towards the sun through a thick atmosphere.
Absorption
This is the process of light transferring energy to the substance via photons. It occurs when light resonates with electron dipole and atom dipole oscillations. A materials transparency domain is determined by alpha where if light is not absorbed then it is transmitted.
Ia/Io = e -α(λ)*l This says that α(λ) the absorption coefficient causes an exponential increase in absorbed light with thickness of the material, l.
Transmission
This is the proportion of light that passes through the material. Generally, transmission is maximized between the resonant frequency for electronic and dipole-dipole oscillators. It is also less for materials with larger atoms (higher n) because of reflection. The size of the atoms is also proportional to the upper and lower bounds of the optical window where larger atoms tend to have an optical window at larger wavelengths.
Conservation of E in light
Io = It + 2nIr + Ia + Is where n = number of panes or interfaces the light is travelling through
Transmission equation
T= (1-R)2 e-α(λ)*z
Parts of an optical window graph
The optical window is a plateau of high transmittance for some materials. The lower and upper bounds are defined by the electronic and vibrational oscillators coupling with the incident light. A more energetic (lower wavelength higher frequency) upper bound indicates a higher band gap and/or a smaller electron cloud. a less energetic lower energy bound indicates larger atoms which need longer wavelengths to oscilate and/or weaker bonds.
The degree to which T approaches 1 is a function of n where the larger the atoms the more light will be lost to reflection.
Coupling
This is the idea that within a classic mechanical model of the world that when the EMR E-fields oscillate at ωo and the EMR transfers energy to the particle or electron to cause an increase in amplitude. When this occurs the iωγ term of n2 dominates γ is the dampening term so T goes to zero
Why is there an optical window and not an absorbance band?
This is because at energies above the band gap there are many different electronic configurations which create incremental jumps with delta E approaching zero. On the other side, although quantized, the jumps in vibrational energies are also very small which make absorption outside the bandgap nearly continuous although with some materials there will be a small hop from the state change
Lorentzian Oscillator: Quantum vs. Classical model
In classical mechanics the system acts like electrons are attached on several springs with some amplitude at a frequency defined by ωo and absorption occurs when light oscillates at ωo
In quantum mechanics there is some ΔE between orbitals proportional to h*ωo and E can be derived from ψ(x). Light is observed when h*ωo =E
Lorentzian oscillator for an isotropic, pure solid like C4
ψ(r) α eikr U(r) where U(r) is the bloch function, a periodic oscillating function that repeats throughout the lattice
What is the value of ψ(r)2 within the band gap?
It is ~0 which indicates that the probability of finding an electron in the bandgap is ~0
critical wavelength
This is the wavelength that the light has enough energy to promote electrons across the bandgap which is synonymous to resonating with the electrons and in both energy is transferred from the light to the electrons.
λc = h*c/eg
Glasses filter out light at wavelengths longer than their critical wavelength.
Which has a larger bandgap, blue or red glass?
Blue glass has a larger bandgap because this indicates that the glass transmits higher energy (shorter wavelength) blue light and not the longer wavelength lower energy red light. Hence black materials (Si) have a bandgap just less than that of visible light ~1.1 eV. If it were zero then it would appear metallic though because all incident electrons would cause transitions.
Why does Si become more conductive when incident light increases?
eg (si) ~1.1 eV ; visible light is in the 2-3 eV range. Thus with an increase of incident electrons there is an increase in the conductivity because more electrons are elevated into the bandgap.
How does ΔE differ between crystals and glass?
Crystals have well defined PE wells. Between atoms the PE increases significantly and near the atom the PE is at a minimum. This means that electrons have well defined bounds and PE states. There is a significantly higher proportion of predefined states where electrons may exist.
Glasses are amorphous by character thus they do not have PE wells within the band gap due to oddities in the configuration of atoms. This means that the potential wells of glass vary and the distribution of electrons at any PE is wide.
Multiphonon cutoff
This is the low energy version of the critical wavelength. It represents the wavelength where at wavelengths less than the multiphonon cutoff, atomic vibrations become the sites of transferring the EMR energy and absorption increases. This decreases with atomic mass.
It represents the point where low wavelength light can cause multiphonon vibrational states so ΔE ~0.
What are the basic components of a Spectrometer?
There is a light source (aim for broad wavelengths), monochromator (grating), and a detector
UV-Vis double bean spectrometer.
This uses a deuterium lamp for λ ~200-300 nm and a tungsten/halogen lamp for λ ~300-2500 nm. It typically employs the use of a rotating mirror to minimize the influence changes in intensity of the source across the source’s wavelength.
They typically use gratings as a monochromator and a Photomultiplier tube or photodiode as a detector. They will have a rotating mirror that continuously shifts between a reference and the transmitted sample light.
Monochromators
These are tools that are used to divide light into its constituent wavelengths to analyze individual parts of a spectrum
Grating equation
nλ = d(sin i - sin r)
n = m = order
d = spacing
i = angle of incidence
r = angle of reflection (angle from normal)
Gratings when n = 0
When n = 0 the resultant light in not a function of incidence. It is specular reflection
Photomultiplier tube
These are more complex light detection devices that have a photosensitive material which interacts with the incident monochromatic light to create a free electron. This electron is accelerated and interacts with various dynodes/anodes to be amplified and the resultant voltage is measured. At every collision the electron is accelerated to produce more electrons from the collision following. Ultimately it creates a measurable current near 100 e-
It is best for low light intensity but is more costly.
Photodiode
This uses a doped semiconductor (PN junction) attached to a voltage to cause a current as a function of incident light. They are cheaper, less accurate, and do not work at wavelengths less than 100 nm (1 micron) where Si is absorbent. They can also lead to false signals due to heat related pyroelectricity.
Why are glasses useful?
Generally we have three options for our optical materials. Monocrystalline material (good optics but hard to synthesize). Polycrystalline materials (bad optics easy synthesis). Glass materials (good optics and easy to synthesize)
Transparency of solids based on band gap
Generally PURE insulators (ionic materials like salt) have Eg = ~8.5 eV which is far beyond the energy of visible light and therefore are transparent
Semiconductors have a mid range Eg = ~1 eV which means that visible light is just over the amount of energy to excite electrons over the bandgap and thus the light is absorbed.
Ruled gratings
Reflective materials that have periodic notches on their surface separated by some distance, d. Incident light reflects differently dependent upon wavelength.
Vibrations: classical vs. quantum
In classical mechanics vibrations are a defined by radians from r=0 and there is a parabolic continuum of energetic states about r=o.
In quantum mechanics there are a series of probabilistic bands at discrete energy levels (n) who are defined by ΔE= h*νo

FTIR wavelength separation
FTIR’s used a michelson interferometer to separate wavelengths for absorption analysis. It is much faster and more accurate than a grating. The reason these are not used within UV-Vis is because they rely upon mechanical positioning which can be accurately done for longer wavelengths but not the short UV-vis wavelengths
Michelson Interferometer
This is a tool for FTIR spectroscopy wavelength-dependent absorption.
First a light source (blackbody radiation) hits a collineating mirror.
This then goes through a beam splitter (50% reflected 50% transmitted)
These beams reflect off mirrors, recombine, go through the sample and are focused on the detector.
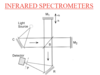
Interferometer mechanism
When the beam of light is split it interacts with two mirrors.
One is fixed. The other moves a distance +- h
This change in distance causes retardation of half of the light. This causes constructive/destructive interference which produces different wavelengths because the blackbody is emmitting a broad band of wavelengths so at a certain position only one wavelength is constructive while the others are destructive.
interferogram
This is a graph of intensity vs. mirror displacement.
If we had a single wavelength of light then this would be a simply sinusoidal curve oscillating between 0 and 1 with 0 intensity when the mirror is at one half of the wavelength.
Interferogram for more than one wavelength
When you add more wavelengths to the interferometer, certain areas constructively interfere and other areas destructively interfere.
For example, if you have 2 wavelengths there is a boudin shaped sinusoid which can be ~broken into two superimposed sinusoids.

Fourier Transform
This is a mathematical tool that leverages the fact that sin/cos waves are easy to differentiate. Because of this, it is convenient to write oscillating functions in terms of superimposed sin/cos waves.
Incidentally, these sin/cos waves, for the use of interferometers, are the original oscillating waves of light that interfere to produce the resultant pattern. This means that the fourier transform “decomposes” the superimposed functions into discrete inputs.
It is like a taylor/mcclaurin series for oscillating functions.
Frequency domain
The frequency domain is the hypothetical space that the results from a fourier transform.
After completing the transform there will be a long summation with a bunch of sins and cosines. Each of these will have a unique wavelength and intensity but in order to understand what each means in terms of absorbance, we convert the unique wavelength to frequency.
Interferogram: Raw data
This will be a plot of intensity vs. displacement. There will be a maximum at displacement=0 because of constructive interference.
It quickly goes to a constant with some bumps at displacement not equal to zero. This can be transformed into wavelength vs intensity.
Processing FTIR data
- collect broadband source interferogram
- collect several interferograms (each takes seconds) to minimize signal to noise ratio
- Fourier transform and convert to I vs wavelength
- subtract out the intensity of the source
- analyze
FTIR light source
Most commonly a silicon carbide coil is resistively heated (pass a current through it) to emit the whole IR range.
Pyroelectric detectors
These are FTIR detectors for high intensity. They are basically solar panels with an IR absorbent material on the surface that heats up the semiconductor and causes a change in potential across the pn boundary. It is an improved thermocouple.
One complication with pyroelectrics is that you end up with a plot of V vs. t that must be aligned to the Fourier transformed interferogram.
MCT
These are low intensity IR sensors used in FTIR. They are made of HgCdTe which are all large, electronically saturated atoms. The photon hits the semi-conductor which excites an electron into conductance. The corresponding change in voltage is measured.
MCT detector needs
An MCT detector requires being constantly cooled (usually with liquid nitrogen) because of the highly sensitive semiconductor used within.
This is because E (temperature) > Eg and is given by E = kbT
What does FTIR measure?
FTIR measures vibrational states of molecules. Different energies cause vibrations which absorb incident IR light. This means that when you subtract the light transmitted vs broadband source you can see where certain sinusoidal functions were absorbed within the sample.
FTIR sample prep
IF IR transparent/translucent
Simply insert into the spectrometer
IF IR absorbent
For an insoluble solid it is ground with IR transparent KBr pellets then pressed into a pellet to be observed.
For soluble solids they are dissolved into an IR transparent solvent and dried onto an IR transparent substrate
Impurity impacts
Impurities within materials can generate additional electronic and vibrational transitions that shift how light interacts with your material.
Why do transition metals color things?
Characteristic d orbital subsplitting creates different energy states that correspond to the energy of visible light. This causes different absorbance as a function of crystal field theory.
Crystal field theory
This is a theory describing why/how materials are colored. For metals within glasses or crystals, they are cations in interstitial tetrahedral/octahedral positions. The complex orbital structure of the d orbitals creates a higher electron density near the anions which means a higher PE state. This causes splitting where certain orbitals are at a higher PE. The difference between these orbitals is given by delta and measured in Dq (difference in quanta)

Optical losses
I/Io = e-αl This says that as light moves through a substance of l thickness there is an exponential decrease in intensity derived from α which is the degree to which the EMR wave is attenuated.
α = f(c[metal+]) as an impurity in the substance. Therefore, a larger concentration of impurity causes more loss.
How does impurity mass impact absorbance
Low mass impurities (ex O or H) generate higher wavelength absorbance because νo = (1/2pi) (k*μ).5
where k = “spring constant” = f(bonding) μ = reduced mass = (1/m1+ 1/m2)
Reflection Spectroscopy
This principally investigates how light interacts with a solid through reflection.
Specular reflection stage
This is a stage that has three mirrors and a sample holder. Incident light hits one mirror reflects off the sample and other mirrors to be routed to the measuring device.
It is an “add-on” component for UV-vis double beam spectrometers and/or FTIR spectrometers.
It is important for the window industry that needs to accurately asses how light is absorbed throughout different light orientations. Additionally it is used for solar cells that need to reflect everything less than 1.1 eV
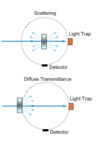
Diffuse reflection integrating sphere
This is a sphere used to determine diffuse reflection which is most helpful when the surface roughness is ~the same as the incident wavelength.
It has a portal that enables incident light to enter. It then reflects on an angled sample so that most of the incident light enters a light trap.
The remaining diffusely reflected light reflects on the highly reflective sphere interior (Au or Ag) until it hits a detector which measures the diffuse reflection.
Total reflectance
This has a sphere with incident light and a sample but the whole interior is mirrored so the detector reads all of the reflected light.
It is used in combination with data from diffuse reflectance and specular reflectance. total = specular + diffuse
Scattering measurements
This uses a diffuse reflectance sphere where the sample is placed in the center and there is a light trap behind the sample. This means that the only light that exits the sample is scattered light.
This is also used to measure the diffuse transmittance of a sample.
These samples require high surface polishing but the measurements help to determine if the nanocrystalline structure is of approximately the same size as the incident wavelength.
Attenuated total Internal Reflectance
This is a tool used for when materials are either too small to use within a typical FTIR or are highly absorbent. It uses an IR transparent crystal with incident IR internally reflected to increase the number of interactions with the sample which increases accuracy.
Evanescent field
This is a tiny E-field (usually <5 microns) that extends beyond the interface during reflection. This means that if you have a sample in this 5 micron interface that it will absorb some of the wavelengths in the evanescent field causing losses in the final reading.
Infrared fibers
These are optical fibers, most often made from chalcogenide glass designed for total internal reflectance of IR light. They are important for evanescent wave spectroscopy because they can be “dipped” into a sample for FTIR analyses.
Number of Reflections for evanescent wave spectroscopy
N(θ, d, L) = L* [tan(90-θ)/d]
where: N = number of reflections
θ = angle from horizontal
d = diameter
This says that as diameter decreases, length increases, and the angle from horizontal increases that the number of reflections increases. This is a design problem though because the smaller the diameter, the weaker the material.
Where is evanescent spectroscopy used?
It is commonly used in biology to measure cells and other membrane-like materials.
Optical losses in fibers
Because l is very large α needs to be minimized. α = f(c[impurity]) so the fiber needs to be very pure.
Measuring α in fibers
The most common method is the “cut back method” where you measure the intensity of light exiting an optic fiber at two different lengths where L1 > L2 and α = [1/(L2-L1)] *ln (I2/I1)
Usually this is done at several different wavelengths because scattering and absorbance is dependent on wavelength
Optical Loss Units
These are reported in dB/length where dB=decibels = 10*log10 (I/Io) where I = output power and Io = input power
This can be used to characterize materials.
1 dB of loss is ~ x% transmission?
1 dB ~ 80% transmission
Losses in Si fiber optics are below 1dB/km
Attenuation in silica fibers
Prior to today, Si fibers only had transmission windows at 1.3 and 1.55 microns because of OH vibrations in water and the general constraints that any solid has for coupling with EMR. CVD has helped minimize the presence of OH impuritites.

Wavelength-division multiplexing (WDM)
This is the idea of using different wavelengths of lasers to transmit different information. They take advantage of low-OH silica fibers to have an optical window from 1.1-1.7 microns which can transmit 100 channels only .2 nm apart (25 Ghz)
Erbium doped fiber amplifiers
EDFAs are fibers that are used to amplify signals in fiber optic cables. Right now the C band amplifies signals between 1525-1565 nm (1.525-1.565 microns) and the L band between 1570-1610 nm (1.57-1.61 microns)
Optical telecommunication networks
These are telecom systems that use a binary format where a laser pulse = 0 or 1. This can be tracked at 100 Gb/sec in a single channel and there are about 100 channels in one fiber using WDM. 100 Gb/sec*channel * 100 channels = 10 Tb/sec
This means that we can transfer information faster than electrons in computers move to process the information. This is why quantum computing would be game-changing.
Dispersion in optical fibers
even with very precise lasers they still have pulses that are not perfectly quantized at one wavelength (usually ~.02 nm in width). Because n = f(λ) and n=c/v this means that at the long path length of an optical fiber that there is a change in velocity between the front and end of the pulse which can cause overlapping.
Point Group Theory
This is the theory that is used to determine the symmetry of molecules and crystals. It is synonymous to crystallography bet with different notation. σ is used for denoting mirror planes where σh is the mirror plane perpendicular to the maximum rotational symmetry (main symmetry axis). σv denotes mirror planes that are parallel with the main rotational axis. Cn is rotational symmetry where n is the number of rotations. The groups are denoted by Dn .
What mechanical behavior is the result of dislocations?
Ductility results from dislocations along the crystal lattice. This is what occurs within metals
Which mechanical behavior is improved by the presence of nanocrystals in a glass-ceramic?
The materials hardness is improved. This is the ability to diffuse stresses through diffuse crack propogation.
What is the effect of an impurity on the electrical conductivity of a metal?
An impurity lowers the electrical conductivity by increasing the electron scattering during the flow of electrons through the materials.
Which has greater electron mobility, glass or crystal?
A crystal has greater electron mobility because the crystal will have discrete patterned structures that lower the probability of electron scattering.
Would a polycrystalline ionic solid be transparent in the visible?
I would expect the material to be opaque because there would be a large amount of reflection due to the polycrystalline nature of the solid.
What are the two main contributions to the thermal conductivity of solids?
There is KL which is the lattice thermal conductivity and is the result of atomic vibrations throughout the crystal lattice transferred via phonons. Materials that do not have rigid bonds have a low lattice thermal conductivity which means they dissipate phonons. For example, diamond has a thermal conductivity of ~1000 W/mC but very poor electrical conductivity. Its strong bonds transfer phonons with ease though.
Ke is the electronic thermal conductivity which is a result of heat generation due to flowing electrons. In metals, most heat is generated from electron flow not lattice thermal conductivity (loose bonds = dissipation of phonons)
What is a phonon?
Phonons are vibrational particles/waves that move along a crystalline lattice and represent heat energy. They are considered a quasi-particle and are quantized as a standing wave through each atom within a lattice having some fixed 0 position.
Types of phonons and character
There are four phonon types:
Longitudinal optical phonons are phonons that move in the lattice vector direction but in opposite directions.
Transverse optical phonons move out of the lattice vector in opposite directions.
Longitudinal acoustic phonons move like sound waves along the crystalline vector
Transverse acoustic phonons move like ocean waves.
Graphite vs. Diamond: structure
Graphite and diamond are allotropes of one another. Graphite has a hexagonal 2d structure with 142 pm bonds in plane and 335 pm out of plane. Diomond is a network solid with .15 nm bond lengths.
Diamond k vs. metals
Diamonds have a thermal conductivity of ~1000 W/mK whereas a metal like copper have a k of ~ 500 W/mK
Graphite k isotropy
In plane graphite has an extremely high value of k (1950 W/mK) out of plane it is very poor (5.7 W/mK) This is because in plane graphite has extremely strong bonds that transfer phonons and electrons well but out of plane both dissapate.
What is the hardest materials?
Diamond is the hardest known material which is why it is used for indentation tests.
Diamond vs. Graphite: electrical conductivity
Diamond is a very poor conductor with sigma=10-16 and a band gap of 5.5 eV. Whereas graphite in plane has delocalized pi bonds which increase its conductivity to 105 and out of plane it is 10
Over what wavelengths is diamond transparent?
Diamond is transparent through the IR and into the UV ending at about .1 microns. This is because it is very rigid and isometric. The rigid means that it resonates with very short wavelengths and the isotropism means that it does not couple with incident IR.
What are the four main types of probes used to characterize materials?
There are visible light (IR-vis-UV), x-rays, ions, and electrons.
What is the momentum of probes?
Light: p =
Wavelength of probes
Light: 12 - .2 microns
X-rays: 1-2 angstroms
Electrons: ~10 pm for 10 keV
Ions: .1 fm for 10k eV
What are the three main components of an optical spectrometer?
There is a light source (tungsten/deutrium lamp for UV-Vis and Silicon carbide blackbody for IR) a monochromator (grating for UV-vis and interferometer for FTIR) and a detector (different photoelectric and pyroelectric sensing devices)
Compare and contrast UPS and XPS
UPS = UV photoelectron spectroscopy; XPS = X-ray photoelectron spectroscopy
Common: They both use incident rays to accelerate electrons and extract them from the sample to give information on the binding energy of the material which is proportional to its structure/composition.
Different: XPS is at a higher energy so it gets information from electrons throughout the molecule of interest whereas UPS only receives information from the outer valence electrons.
What probes are used for structural analyses? How do they compare/contrast?
Generally neutron diffraction, XRD, and TEM.
These all are similar by using diffraction patterns to determine the structure of a material but differ in the types of probing energies used. Nuetron diffraction and XRD both diffract a crushed powder to create intensity as a function of angle. TEM transmits electrons through a very thin part of the sample to receive informaiton.
What are the two primary ways to describe light?
Light can be described as either a wave (with velocity, wavelength, and sinusoidal intensity) or as a particle (with a defined quantized amount of energy in each photon)
What is the proportionality constant between the electric field and the polarization and what are the three contributions to polarization?
P = εo Χ E
Χ = dielectric susceptibility = f(material) = how electrons do not transfer but shift relative position
εo = the electric permittivity of a vacuum = C1
E = the strength of the oscillating electric field.
P = polarizability = the density of dipole moments within a confined volume.
What are the three main contributions to polarization and how do they function in relation to wavelength?
Rotational oscillations occur in long wavelengths beyond the IR. They are limited to gasses and some liquids where crystallinity does not disable rotational degrees of freedom.
Vibrational oscillations occur between atoms of a molecule and between molecules. They represent heat transfer due to incident IR.
Electronic oscillations are the coupling of incident EMR and electrons. They occur mainly in the UV/vis range of light depending on the unique structure/composition of the material where an atom with a greater bandgap (proportional to bond strength) will only couple at higher energies because this is the energy needed to elevate the electron into the conductance band.
What are the four main effects observed when a beam of light is incident on a material?
There is scattering, reflection, transmission, and absorption.
How does the refractive index depend on the composition of a material?
n = [(R-1)/(R+1)]2 and atoms that have more electrons in their conductance band where incident light is returned have greater reflectance.
Why do certain pure semiconductors exhibit color?
This is because some semiconductors cutoff wavelengths within the visible region. The lower the bandgap of the material the longer the wavelength of the material that relates to the cutoff wavelength. Thus a red glass has a lower cutoff than the yellow.
How does a grating work?
A grating works by the property of light diffracting off a surface. It has notches or grooves with a “d” spacing that creates constructive and destructive interference based on the wavelength and spacing.
In mathematical terms this is given by d(sin i - sin r) = m*lambda
Where i is the incident beam from normal of the grating and r is the reflected ray from normal.
What types of detectors are in a UV-Vis spectrometer?
UV-vis double beam spectrometers typically have either a photodiode which is basically a solar panel (cheap, rapid, less accurate due to heat) or a PMT, photomultiplier tube (accurate but expensive. These work through having a photon hitting a photosensitive surface which emits an electron that is accelerated by dynodes and anodes to emit more electons to create a charge that is measurable.
What kinds of energy levels are typically probed with a UV-vis spectrometer?
Within the UV-vis range (1-5 eV) you will be probing electronic transitions in the material by observing what is absorbed vs transmitted. This correlates to the material’s bandgap.
What are the two steps required to obtain an FTIR spectrum?
In FTIR spectroscopy you need to take the raw interferogram, conduct a fourier transform, then subtract it from your original broadband source spectrum.
What is a Michelson interferometer and how does it work?
This is a monochromator used in FTIR spectroscopy that operates by having a beam splitter and two mirrors. One of which oscillates position.
The beam splitter sends half of the light two both mirrors and the oscillating mirror retards the wave. This means that upon merging the two waves that they are out of sync and destructive interference destroys certain wavelengths (because you are using a broadband source)
Types of FTIR detectors
Principally there are pyroelectric sensors which are fast but not the most accurate and are specialized for high intensity incident light. These work by basically having a pn junction but the semiconductor is excited by incident IR and not light.
MCT (mercury cadmium telluride) sensors are also used for low intensity light (like with evanescent spectroscopy) but are cumbersome because they need to be cooled with liquid nitrogen and are extremely sensitive. They operate through having a photon hit a semiconductor which excites an electron into the valency band.
What kinds of energy levels are typically probed with FTIR?
These are most typically vibrational. For our investigation of solids these are vibrational. These typically correspond to energy levels in the ~1-2 eV range.
Can different molecules have the same vibrational spectrum?
Materials of different composition/structure will not have the same vibrational spectrum because their crystal lattices are dictated by different bond strengths and configurations which determine how molecules vibrate and the wavelengths they couple with.
What is the common method used to collect FTIR as a function of material type.
If materials are transparentish they can be inserted into the FTIR just like any other sample.
If they are insoluble they are crushed with KBR pellets (transparent to IR) and compressed to then be analyzed.
If they are soluble they are dissolved into an IR transparent solvent and put onto a thin film.
Why is Si transparent in the mid-IR and SiO2 is not?
SiO2’s multiphonon cutoff is in the high IR range which is where Si’s cutoff wavelength for electronic transitions is. This means that in he mid-IR Si has electrons that are not excited across its bandgap but it is also not oscillating due to incident IR, making it transparent because of a lack of coupling.
In comparison, SiO2 has much more rigid bonds meaning it oscilates at higher frequencies but also has a larger bandgap, shifting its optical window to the righ.
The number of vibrational modes in linear and non-linear molecules?
non-linear molecules have a number of vibrational modes given by 3N-6 where N is the number of atoms in the molecule. Linear molecules have a number of vibrational modes given by 3N-5.
How many vibrational modes does CH4 have?
CH4 (methane) has 5 atoms in its structure and is non-linear hence it has 3*5-6 vibrational modes which is 15-6=9
Why does methane have a 9 vibrational modes but only 4 peaks?
Many vibrational modes are the same dipole oscillation in different directions. Therefore, because the magnitude of the change in dipole moment is equivalent, there are equivalent resonant frequencies for each of these modes. This means that there will only be 4 frequencies of light that couple with all 9 modes.
How to determine point group based on symmetry?
You use a flowchart to determine the point group. these are then used to describe characteristics of the symmetry using character tables.
Selection Rules for FTIR and Raman
Because raman is measuring an energy state change and not a coupling of the photon, raman active vibrations are quadratic or do not produce a dipole, vibrations are symmetric. In comparison, FTIR relies upon the absorption (coupling) of light through having a photon at a resonant frequency which means that the vibrational state must induce or enhance a dipole change.
What vibrations are FTIR active?
The atomic motion of an induced vibrational state must induce a dipole moment change to be IR active.
Reading Character tables for IR vs. Raman
On the right side of the character tables (these describe the different vibrational oscillations of a point group), there are two+ collumns. The first will have x, y, z, Rx… These are linear vibrational oscillations which couple with IR light. To the right are some function that includes variables multiplied by one another. These are quadratic vibrational oscilations which are only probable using raman.
Raman Scattering
When light penetrates a material the oscillating EMR can cause osilations of the electron cloud at the same frequency of the incident light. This is the acceleration of a charged particle which is the same as light. When the molecule returns to a ground state this then re-emits light of the same frequency as the incident light in various directions. Importantly, no energy is transferred during the interaction.
Rayleigh scattering
This is the most common form of light scattering and is characterized by light being scattered at the same wavelength as the incident light which also means there is no net change in energy of the molecule under inspection
Virtual State
This is the “state” of electrons during the scattering process where they are not elevated to a particular energy state of the material but are instead elevated to a non-real state above their vibrational levels. This is because the incident light is in the visible range (2-4 eV) which is at an energy much larger than the vibrational states which are closer to 100 microns.
Anti-stockes scattering
This describes scattering where the electron is starting in a higher vibrational state (from heat or other energy sources) and is elevated into the virtual state by the incident light. After the electron is elevated, it returns to the ground state. This means that it emits light at a shorter wavelength than the incident light that it interacted with. This only occurs in a very small proportion of interactions.
Stockes scatterring
This occurs when light interacts with a material, it moves from the ground state to the virtual state and down to an elevated state that is at some energy above the ground state given by E = h *v where v is the frequency of a vibrational mode. This means that the scattered light is of lower wavelength than the incident light.
Why does raman spectroscopy not measure induced dipole changes?
Even though both IR and raman measure vibrational modes, because raman is NOT coupling with the atoms in vibrational states, it does not transfer energy which requires electromagnetic fields to oscilate with something, like a dipole.
Raman Shift
Raman works by irridating a sample at some wavelength of light and measuring the scattered light. Because rayleigh scattering is the most common form of scattering, the wavelength of highest intensity will be that of the incident light. Raman shift represents the difference in wavelength of the Stocke’s/anti-stocke’s shift in the scattered light due to vibrational energies.
E = hv=hc/λ and because hc=constant, raman shift is presented in 1/λ.
What does a full raman spectrum look like?
A full raman spectrum will have intensity on the y axis and raman shift on the x. There will be a really tall peak in the center (Rayleigh scattering). On the left (shorter wavelengths) are the anti-stocke’s scattering. On the right will be slightly more intense but mirror images as the Stocke’s peaks.
Intensity of stockes vs. anti-stockes
The number of atoms that are in a vibrationally excited state within a given volume is proportional to Et = kbT. The occurrence of scattering is scarce and the number of these elevated states interacting with incident light is exceedingly rare. This being the pre-requisite for anti-stockes scattering means that the intensity of anti-stockes peaks is low. In comparison, it is much more likely to have an atom enter an excited state and not return to ground state. Thus the intensity of stockes peaks are greater than anti-stockes.
Morse potential
This describes the anharmonicity of atomic oscillators. Generally, atoms can diverge to infinite distance but cannot converge to 0. Hence in a chart of the internuclear separation vs energy, the energy approaches an asymptote (dissociation energy) at large distances and approaches infinity at low.
Anhamonicity relevance
Because of anharmonicity, the difference in energy between vibrational states rapidly decays for a true atomic oscillator. This is because as oscillations broaden there is a greater probability of finding an atom in a vibrational state of only slightly higher energy. This is an additional reason why after the multi-phonon cutoff it is complete absorption and not a peak.
How does temperature effect raman spectra?
An increase in temperature will reduce the intensity of stockes scattering and also bring the wavelength closer to the laser line. It increases the intensity of anti-stocke scattering and also brings it closer to the laser line with a broader peak. This occurs because in both cases there are more atoms already in a variety of vibrational states which means that the ΔE from the virtual state to the vibrational states being observed via raman shift is less.
Raman spectrometer layout
There is an Ar ion laser that interacts with a beam splitter. half of this light enters a microscope that focuses it on your sample. This microscope also gathers the scattered light which is passed through a notch filter, a grating, and ends up being measured by a CCD detector.
Notch filter
The notch filter is a specialized filter that removes the rayleigh line from the scattered light.
How do lasers work
Lasers have a chamber of some inert gas or material that has a large amount of energy put into it. This causes simulated emission in random directions These reflect off two parallel mirrors, interact with the material and some of the stimulated light is directed out of the outlet.
Critcally the length of the chamber is n*lambda
Charged Coupled Device (CCD)
This is a simple Si semiconductor where the photon hits the PN junction, excites an electron into the conduction band and the resultant change in voltage is measured.
Within a raman spectrometer there is a linear array of CCD’s that collect several wavelengths off the grating simultaneously.
Why is there a “forest” of peaks around FTIR gas spectra?
The reason the peaks of the FTIR have forests around them is that they have rotational freedom which enables them to have many “sub-levels” near the vibrational levels.
How do bending modes couple with frequency?
Generally, bending modes occur at a lower frequency because they involve a greater change in inertia than symmetric stretching modes that can oscillate very rapidly.
Degenerative modes
This alludes to bending types with 1 frequency. Generally, similar types of vibrations (stretching, bending,…) have the same natural frequency. This is because they may be the same motion but within a different plane.
Gas, glass, polycrystalline, and crystals in spectra
gases will have a “forest” of sharp peaks related to rotational modes near their vibrational modes.
Glasses will have lumps and humps related to less discrete vibrational states and long range disorder. They will also be less distinct between FTIR and raman because many of their bonds are distorted which can either decrease or increase asymmetry in the oscillations.
Polycrystalline material may also appear quasi-glass because at the surface of the internal crystals the structure is not discrete hence the spectra is distorted.
Crystals will have well defined and sharp singular peaks.
Reading Character Tables
E denotes degeneracy (how many modes have the same symmetry, based on the symmetry of the molecule’s vibrational state
i = center of symmetry. IF i = 1 then the center of symmetry does not change during vibrations. IF i = 2+ then the center shifts during oscilation and if i<0 then the oscillation is assymetric and symmetry is broke.
FTIR vs. Raman spectra
If you compare FTIR vs. Raman you can see how different vibrational modes couple with EMR.
If there are peaks for both FTIR and Raman then the vibrational mode is symmetric but a dipole is present. If it is only raman active then the vibration is symmetric without a dipole. If it is only FTIR active then it is assymetric and induces a dipole.
Lattice Dynamic
This is the idea that phonons within a crystal create cooperative discplacement which means that when molecule oscilates it also influences all of its nearest neighbors. Within crystals this creates short-range (1 neighbor), medium range (~2 neighbors), and long range (3+ neighbors away) symmetrical oscilations.
In comparison, within glasses there is short range and some medium range order but the lattice dynamic is not as relevant.
When to use the intensity ratio of stockes and anti-stockes?
You use the intensity ratio when there is fluorescence. This is because fluorescence will dominate the stockes side of the spectrum.
Phonon disperion and desnity curves
This is the exact same type of diagram and the band gap diagram for electrons. It solves schrodingers equation for phonon propogation by wavevector. Then at each energy state the number of phonons that can be at that state is considered the phonon density. This will show a gap where phonons cannot occur just like the bandgap diagram too.
Diamond oscilation modes (raman)
Within diamond there is one peak because there is one mode that is symmetric (symmetric stretch) this will not show in IR though.
Polarized Raman
This is a specialized version of raman spectroscopy where you measure some of the anisotropic properties of a crystal lattice by having the incident EMR oscilate in one plane of the lattice. This is more complex though because you can no longer use a microscope objective to focus the light and collect scatters (light is not longer colinear). It also requires using a single crystal for inspection to align the cystallographic axis. Generally it produces a low signal:noise.
General types of polarized raman
There is generally circular polarization (like a helix) and plane polarized (B and E at 90o from one another)
Advantage of Polarized raman
Using polarized raman you can determine the individual components of the diaelectric susceptibility tensor.
Raman with composition
The relative intensity of peaks can be used to determine the composition of a material’s impurities by concentration.
What is the origin of satellite peaks on the vibrational spectra of gases?
These “forests” of peaks are caused by rotational oscilations of the gas and the incident light. This is unique to gases which have the rotational freedom for such movements
What are the two reasons that an FTIR spectrum for a molecule has few peaks than we would predict from the number of oscillation modes?
There are degenerative modes of vibration that means that different vibrational modes have the same resonant frequencies
FTIR couples with materials which means that there must be a change in the dipole moment of a material. This does not occur within vibrational mode.
Does stretching or bending have a higher frequency? Why?
Bending occurs at lower frequencies because it takes less energy (bond length is about the same) and requires a lower change in momentum.
Stretching involves a change in the bond length which acts similar to a spring. This means that it takes more work to extend and compress the “spring” with each oscillation and there is also a stronger restoring force which means that the coupled light has a higher frequency in order to match the resonant frequency and to oscillate with the rapidity of a stronger restoring force.
What is a point group and character table?
A point group is a name that summarizes the symmetry elements of a molecule or a material. A character table lists how configurations with this symmetry can vibrate/oscilate with respect to their symmetry and dipole moments.
What is the requirement for a vibrational mode to be IR active?
In order to be IR active, the vibrational mode must have a change in the dipole moment. These are also known as linear modes.
How is vibrational energy calculated from a raman scattering spectrum?
Even though the sample is being irradiated by visible light and emits visible light, a sample that undergoes anti-stockes or stockes scattering will emit visible light with a different energy than the incident light (some will be transferred to oscilation in the case of stockes) This means that the difference in energy of the received light and the incident light indicates the energy transferred to cause vibrations.
What is the effect of anharmonicity on vibrational energy levels?
Vibrational anharmonicity means that as vibrational levels increase the change in energy between quanta decreases to the factor of 1/2. This means that within materials that are warm and have parts in these elevated vibrational states that the spectra will be less sharp and more lumpy because there is a greater range of small deviations in the vibrational states.
What is a notch filter?
A notch filter is a highly specialized filter designed to omit the rayleigh scattering line from the spectrum.
Why do Raman spectrometers use lasers instead of broadband?
In raman you are measuring a difference in incident energy and scaterred energy. Scattering first is a rare phenomena and needs a high intensity source. Second is that by using a finite source you are able to better measure how the scattered light energy deviates from that of the incident light.
Do you expect the Raman spectrum of CaCO3 to have more peaks than diamond? Why?
Yes, I would expect all forms of calcite to have more peaks than diamond becuase there is greater heterogeneity within the structure. This means that there are several more modes of oscilation within the lattice dynamic. In comparison, diamond is homogenous which means that it has very finite oscilations.
Atomic Force Microscopy
Atomic means that it measures down to the level of a singular atom (technically sub-atomic)
Force means that the technique uses force and is not optical
Microscopy is a surface imaging technique which creates a topological map of the surface of a material
Together, this means AFM describes a method of analyzing the topology of materials at the resolution of singular atoms using a force technique
What are the components of AFM?
The sensor/probe is the tip and cantilever.
The positioning instrument (~monochromator) is the scanner stage or piezoelectric cells. These measure x, y, z.
The detector/control unit is the laser and photodiode
How does AFM work in principle?
There is a piezoelectric scanner that controls x,y,z motion of a cantilever beam with an atomically sharp tip. A laser is reflected on the cantilever towards a photodiode that measures voltage as a function of the position of incident light. This is because we can measure/control voltage to a high precision.
The photodiode information is fed to a computer that integrates the information, find the rate of change (derivative), and compares proportionally to reposition the scanner until the error signal = 0 while also relaying that information to the scanning probe to produce the topological map ouput.
Basically, it raster scans the sample down to atomic resolution.
AFM contact modes
There is contact mode (physical contact with sample), non-contact mode (oscillate tip and notice dampening due to Van der Waal’s forces), and tapping mode (occasional contact)
Why is AFM versatile?
- ) a variety of modes of detection enables testing of a wide variety of materials
- ) different types of piezoelectric scanners can alter the resolution of the images dramatically. This ranges from 20 microns (like a DVD) down to ~1x1 nm nanotubes
- ) It is straightforward. No vaccums, little sample prep, and is a small machine with atomic resolution.
Compared to other techniques (TEM requires a vaccum and a sample less than 100 nm thick and SEM does not have atomic resolution) this is a much more adaptable and usable technique for gather data.
Contact vs. non-contact modes of AFM: working principle
Contact Mode: Beam deflection is proportional to force given by -kd where k=constant and d=deflection. Deflection is measured on the photodiode’s quadrants and the error signal is reduced to zero to make the force constant while scanning the sample. Even though called contact mode it is actually deflection based on repulsion at a sub-atomic level.
Non-contact mode: You use a high frequency potential generation tool to maximize the amplitude of oscillations of the cantilever (this is “matching” its natural frequency. Like slapping a ruler). When the tip comes between 10-100 angstroms of the sample, Van der Waals forces dampen the oscillations which are measured through the reflected laser/photodiode. This is fed to the computer, probe reoriented, and topology produced.
Error signal
When scanning a sample using AFM the error signal is given by the difference between the actual signal measured and a predefined input signal (control). The difference between these signals is proportional to the force or dampening of the tip/cantilever and is used to adjust the position of the probe. Repositioning is done until the error signal is 0 (so force/oscilations are constant)
Contact vs. non-contact: When to use
Non-contact is best to use on hard samples (like metals or nanocrystals) because if you use contact mode your tip will rapidly where down which is expensive and produces poor image quality.
Contact mode is best to use with live things or wet things (ex: cells) because oscillations will be dampened by the environment and not the sample which would make your results unreliable. A concern of contact mode is making sure that the scan is occurring slow enough for the error signal to be minimized. If this does not occur then the sample will get a trench dug through it from the tip.
What types of crystals are piezoelectric?
Non-centrosymmetric crystals (like perovskites) are piezoelectric. This is because at low temperatures their center atom (Zr or Ti) is smaller than the site that it sits within. As a result it moves to the upper or lower part of the crystal creating a permanent dipole. Henceforth, if you apply a voltage to a rock, the dipole will amplify and deform. It also produces a current if deformed.
How does a piezoelectric tripod scanner work?
This has three (usually ceramic) piezoelectrics in the x, y, z directions which are used to position the tip and scan across the surface. They usually use large columns which make them ideal for larger scanning (~100 microns). Voltage is applied to each of the collumns to change the position of the probe.
Tube piezoelectric
These are tubes with 4 piezolectrics on the outer edge. Through applying voltage evenly to all of the piezoelectric dz can be induced. Through applying voltage differently, the tube can be bent and small areas scanned. This is used for small areas of scanning in high resolution.
Position Sensitive Photo-detector (PSPD)
This is a CCD sensor with 4 quadrants. Each quadrant has a simple photodiode (pn junction) but is individually wired. This enables the input signal (the laser for AFM) to be measured as a function of location. This is the principal mechanism for AFM’s to ensure the proper oscillations or constant force because when perturbed (light not being distributed evenly on the sensor) an error signal is produced and the computer adjusts the voltage to mitigate the error.
Z resolution of AFM
Because we can control piezoelectric incredibly well, the resolution of AFM is sub-atomic.
In the z direction this is down to angstrom high deviations. It is limited by electronic noise and mechanical vibrations.
x, y resolution of AFM
The x, y coordinates of AFM depend upon the roughness of the sample under analysis. Atomically flat samples have “ultra high resolution” that is down to the diameter of singular atoms. Samples with surface roughness have “medium resolution” which is proportional to the quality of the tip and its geometry.
Piezoelectric crystals with temperature
At high temperatures (above the Currie temperature) the atom in the center of the crystal structure has enough kinetic energy that is oscillates rapidly about the center position. This eliminates the dipole on a macro scale. Below the currie temperature the atom in the center no longer has the KE to be displaced and thus oscillates to one side or the other creating a permanent dipole.
Piezoelectric crystals chemistry
These are usually perovskites (Pb (Zr,Ti) O3) which in 3d is a face-centered cubic with an octahedral Zr4+ or Ti4+ in the center. Because both of the cations in the center have very high charges the atoms are very small. This is what enables the ion to change position. It does not fit into the site.
Scanning Tunnel Microscopy (STM)
This is a form of non-contact AFM limited to conductive materials. It uses the ability for electrons to “hop” over a small potential barrier gap (when a potential difference is applied aka voltage) to measure the current as a function of topology where a decrease in distance = less distance between tip and surface.
There are two modes, constant current (feedback system maintains a constant difference in height between the sample and tip) and constant height (current changes but the z position of the probe is constant).
Tunneling Current
Tunneling is a quantum description of electrons where electrons are described by a standing wave wavefunction. The probability of finding the electron in the sample is high and the probability of finding it in the tip is low but there are a proportion of electrons with enough energy to make the hop favorable
There is an exponential decay of the probability in the gap which represents a small potential barrier. If the electron “hops” over the potential gap it creates a current in the tip.
Tunnelling Current formula
I ɑ Vρe-2KW
Where: I = the current in the tip
ρ =the local density of the sample (density at the sample surface)
K=wave function decay in the barrier
V=voltage
W=potential barrier width (m) This is the most important variable
STM Constant Current
This is a mode of scanning tunneling microscopy where the tripod piezo scanner rasters the sample while maintaining a constant current. It is used for rough materials where it is not feasible to be at a constant height because of the large topography. The change in current is closely tied from the distance between the tip and the sample so the error system measures changes in current and adjusts the z-positioning of the probe as needed so that error=0 based on some standard current which is the control.
STM: Constant Height Operation
In this mode of scanning tunneling microscopy (reserved for minimally rough samples) The piezo maintains a constant absolute elevation and the changes in the distance between the tip and the surface of the sample changes the current. These changes in current are used to back-calculate the elevation of the surface.
STM: Single Atom Manipulation + Imaging
Because atoms are charged particles and scanning tunnelling microscopy is founded on principles of electric charge differentials, this can be used to move single atoms at very cold temperatures (4 K). This is used to practically understand how specific atoms preferentially align with themselves
Scanning Tunnelling Spectroscopy “quantum corrals”
This is a concept used to prove quantum mechanics. You create a “corral” of small atoms (H) because this will create a potential energy wall where an internal atom’s electrons will be restricted to acting as standing waves.
To measure this the AFM varies both current and voltage to ID how the electronic density of state changes within the corral.
Near-Field Scanning Optical Microscopy
This is an AFM related technique where the tip is a silica fiber that a laser is sent through. This is transmitted through the sample to collect the sample’s refractive index over the area while the tip uses the non-contact mode of AFM (changes in frequency) to measure the topology.
It has a resolution dependent on the numerical aperature of the tip (~10-100 nm) and typically yields nm spatial resolutions.
Diffraction Limit
This is the minimum waist diameter of a beam of light. It is usually half of one wavelength. This poses an issue for classical optical microscopy where the size of materials able to be observed cannot be less than half the wavelength of light.
This is why most visual microscopes have a maximum focus of ~1 micron.
How does near-field scanning optical microscopy beat the diffraction limit?
The probe has a silica fiber coated by aluminum (causes reflectance). This has an atomically sharp tip that “funnels” light to a diameter that is smaller than half of the wavelength. This is important for nanocrystalline materials and PN junctions where the area needed to be optically analyzed is less than 1 micron.
Why does NSOM operate at a constant height?
This is because light diffracts, and the exiting ray increases exponentially with distance beyond the minimum aperture (d α r4) . Thus the probe operates at a constant height so that the optical observations can be as precise as possible. This also influences the van-der-walls forces acting on the tip so maintaining a constant height also ensures accurate topology.
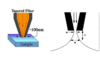
Types of NSOM
There is a transmission mode where the light transmits through a material and that light is used to make optical observations. In this mode n is mapped by how transmission changes. Alternatively, the sample reflects the light and optical information is observed through the reflected rays. The reflected mode has the advantage of being able to determine a change in n because R is proportional to n which critically gives information on the composition.
Near-field scanning fluorescence
This is using near-field microscopy to observe fluorescence within materials. This can be used to identify how certain fibers change with strain, where certain elements exist/coagulate for medical diagnosis, and how materials organize themselves.
X-ray Diffraction (XRD)
This is a very common technique that uses the basic concepts of the single slit experiment to understand the 3D crystallographic structure of a substance (d-spacing and unit cell parameters). The diffraction pattern (which waves constructively vs destructively interfere) is a function of the spacing of atomic planes within a crystal structure.
Because this technique relies on having a well-ordered material with consistent atom spacing it is applicable to crystals and the short-range order of glasses only
Joint Committee on Powder Diffraction Standard
This is an international organization that collects a “seed bank” of XRD patterns. This collection can then be used by individuals to match their scans with the standards and determine their sample’s composition
Crystalline structures
These are periodic arrangements of atoms. The Unit Cell describes the smallest arrangement of atoms that can be repeated to infinity without having gaps/holes in the crystalline structure. These define the crystalline lattice of the macrostate.
There is a finite number/ways to create unit cells. These are described by the 7 crystal systems (symmetry of 3-space) and 14 Bravais lattices (changes in the origin of the unit cell)
Miller Indices
This is a way of describing planes within a unit cell. they are given by [hkl] where each letter is the inverse of the unit cell length intercept in the order of abc. These are used because to determine d-spacing, the relative intercepts of planes defines their placement within the structure.
Ex: if a cubic unit cell with ao=10nm is intercepted along the a axis at 10 nm, the b axis at 3.33 nm, and c at 5 nm then abc = 1, 1/3, 1/2 and hkl = 1, 3, 2
How are miller indices related to d-spacing
Each plane defined by a miller index can repeat infinitely throughout the crystalline structure. These planes will be separated by unique d-spacings based on the cell characteristics.
Determining d-spacing (cubic and others)
for a cubic cell dhkl = ao / [h2 + k2 +l2](.5) This is really simple because each of the sides is of equal length so there is no need to change the weighting of each index.
Low symmetry crystals have very complex calculations based on both the non-orthogonal nature of their principle axis and their different cell lengths along each axis.
In practice the cell parameters are determined by finding the d-spacing of the crystal as a function of theta. Then guess the cell parameters and miller indices for each reading. This creates a system of equations that finds hkl values that satisfy each d-spacing measured.
How do the number of XRD peaks change with crystal symmetry?
As symmetry decreases, the number of reflections increases and the peaks split. This means that the singular peaks of a isometric crystal become forests within triclinic or orhorhombic crystals.
Rietveld Refinement
This is a measurement reserved for very complex crystals (in powder form) where the elemental composition is predetermined but the structure is not. XRD intensity is a function of d-spacing and atomic composition. This method uses compositional data to model the structure which is then compared to real data and fitted to minimize error.
JCPDS Card
This is a standardized card that is used to catalog the XRD measurements of crystals. It includes information on the chemical formula, the quality of data, crystallographic data, optical data, diffraction, and sample data.
Near-Field Polarizability
This is a type of near-field scanning optical microscopy that analyzes how light polarizes through a material by placing a polarizing filter below the transmitted move of NSOM and rotating the beam until the polarized light matches and is transmitted. This is used to understand how strain influences fibers.
X-ray tubes
These are the things that produce x-rays. They work by having a tungsten filament that has a great amount of current ran through it to create free surface electrons. There is a large potential difference (usually 50 kV) between the tungsten filament and the target (a transition metal like copper) which accelerates electrons over the gap and bombards the target and creates x-rays.
These are then funneled through beryllium windows to iridate the sample.
They operate in a vacuum in order to ensure that the electrons do not bombard gas molecules and also need to be constantly cooled using water in the back.
What are the needed x-ray characteristics for XRD?
x-rays need to have a well-defined wavelength because the measured d-spacing is a function of the wavelength. Additionally, if the wavelength is too long then the rays will not be able to resolve the structure.
What are the basic components of AFM and its principle?
AFM principally has a probe tip (usually silica etched to be atomically sharp), a device for measuring deflection or changes in oscillations, a piezoelectric for positioning, and a computer to actively conduct error minimization/signal processing.
It works by taking into account the interactions of matter and the tip at subatomic levels to understand the surface topology and other potentially relevant information.
What is the resolution range of AFM?
In the z direction it is about one angstrom (limited by vibrations and electronic precision) In the x and y directions it is less than one angstrom
How are monochromatic x-rays produced?
X-rays are produced using an x-ray tube. This produces two characteristic x-rays, Kα and Kβ which correspond to the grounding of electrons from the L to K level and the M to K levels. The Kα intensity is much greater than the Kβ which is based on the probability of an electron dropping to the n=1 level. A filter of a heavy metal is used to absorb the Kβ rays which is a function of the target metal (The filter is usually ~2 atomic numbers less than the target)
Detector in XRD
This is a scintillation counter with includes a scintillation crystal (Tl doped NaI) which emits visible light upon absorbing x-rays. These are then funneled into a photomultiplier tube and the intensity measured. Because XRD is measuring the exit energy of the x-rays, the need to differentiate visible light by wavelength is uneeded.
Scintillation crystal chemistry
These are ionic substances with large transition metals. The large bandgap of ionic substances makes them good for absorbing x-rays and the transition metals help “trap” moving electrons so that way there is not a strong charge imbalance.
Bragg’s Law
This is the law that defines constructive and destructive interference. In principal it argues that if the phase of waves align (change in path length is equal to an integral number of wavelengths) then constructive interference occurs if the phase is off by pi then destructive interference occurs.
In XRD it means that planes that reflect in a way that the difference in travel paths is an integral number of wavelengths the reflections will constructively interfere.
nλ=2dsin(
Bragg’s Law: Math
nλ=2dsin(θ)
where n=1 because we are only concerned with first order diffraction
d=d-spacing of planes within a crystal
θ=angle between the detector and the incident x-rays
Laue Method
This is an old fashioned method of singly crystal XRD. It uses a broad-band (white light) source which is filtered through lead, intercepts a crystal and creates a diffraction pattern captured on a photographic plate. This probes all planes within the singular crystal because all wavelengths are present.
It produces a plot of dots which are the result of constructive interference defined by Bragg’s law. With complex math you can solve for cell parameters based on the resulting image.
Modern single crystal diffractometer
This uses a monochromatic ray source that interacts with a single crystal attached to a needle. The crystal is rotated throughout all orientations and intensity measured.
What are the typical values for Kα?
Kα is usually slightly less than 2 angstroms (Cu=1.5) Generally the more electronegative the metal, the lower the wavelength it produces.
What is the process of creating x-rays within an atom?
Within an atom, the innermost electrons (K-level) are ejected through a transfer of kinetic energy from the incident electron to the core electron. This vacancy is then filled by an outer core electron and the potential energy difference between these two electronic levels corresponds to the x-ray area of EMR.
Powder XRD
This is the most common method of XRD where a sample is ground to fine size (<100 microns) and then analyzed via normal XRD methods. This has the advantage of being able to represent all of the different d-spacings in a crystal without having to probe from every direction because each particle contains thousands of planes and the thousands of grains will represent almost all planes
Powder XRD: Relationship between θ and the incident beam
The incident beam intersects the sample at an angle of pi-2θ. This is because θ is measured from the exiting ray to the diffracted beam not the incident beam.
Diffraction Cones
If we imagine there are several thousand particles within the sample that is being probed, where there is a large number of grains with 2θ which matches Bragg’s Equation then, in 3D a cone of constructive interference is created. This is because we can consider the incident beam as a vector and hence the geometric shape that describes an angle from a vector is a cone.
Detecting diffraction cones
In power XRD, you create cones that represent the d-spacings present in your sample. By scanning in a semi-circle collinear to the incident beam you intersect all of these diffraction cones and hence can have I vs. 2θ in one sweep.

Debye-Scherrer Camera
This is an old-fashioned method for doing powder XRD. It involved setting a sample inside a hoop of photo-sensitive paper. This hoop intersects the diffraction cones and record their 2θ with the relative intensity being proportional to the darkness of the line on the material.
Modern automated XRD powder instrument
These have a big base with two large gonimeters on the front. Both the detector and x-ray tube is mounted onto this and rotate about the sample held within at the axis of rotation. The angle between the source and detector is pi-2θ
Ideal particle size for powder XRD
The ideal size is between .1 and 40 microns.
If the sample has particles less than .1 microns then peak broadening occurs, if greater than 40 microns then particle d-spacings are probed more than others and the results are not accurate.
Ways to prepare powder XRD samples
- Deposition method: In this method you spray a fine layer of wax (amorphous so no signal) and “sprinkle” a fine layer of your sample on this
- Slide: This is more common and involves heaping the sample into a hollow holder and then scraping off the excess.
Prepping powder XRD: Mistakes to avoid
DO NOT pack the sample, this will cause preferred orientations of crystals which distorts intensity.
Make sure the surface is as even as possible with the slide. The detector is calibrated for 2θ based on the upper surface of the holder and if over or underfilled, 2θ will not be accurate.
Preffered orientation in XRD
Cleavage and packing may make they crstals align within a prefferred orientation which can distort peak intensity. This is very important for Rietveld Refinement where both the 2θ and intensity of peaks is used to construct the model of the structure.
FWHM
Full Width at Half Maximum is a measure of how broad the peaks are. Imax defines 2θ and the θ width at Imax/2 is the FWMH. It depends on grain size and residual strain.
Residual strain impacting XRD
IF strain is homogenous (compaction) then the width is constant but θ shifts to a lower value
If the strain is non-homogenous (bending) then the peak remains at the same value of θ but is much broader
Instrumental error in powder XRD
X-ray source: Because the n=2 orbital has both s and p shells there is truly two wavelengths bombarding the specimen which creates a finite peak width. The beam size also impacts width.
Goniometer Optics: The focusing and/or slit size which is used to create a finite beam can be imperfect and cause 2θ to deviate within the incident beam. Additionally, any penetration into the sample will cause for a deviation in the calibration.
Peak Width formula (Scherrer Equation)
B(2θ) = K*λ / L*cosθ
Where B= FWMH
λ = incident wavelength
K = scherrer constant (material dependent but ~1)
L= diameter of the crystallite which is NOT the diameter of the polycrystalline grain.
Powder XRD Reactions
Powder XRD is useful for also understanding reactions. You can use a heated sample holder to observe phase changes over time at a constant T, phase changes with increasing T over time, and crystallization rates over t and T. For example, you can basically watch the process the a glass crystalizing using a heated powder XRD machine.
Why does TEM use electrons?
Typical microscopy is limited by the diffraction limit which is equal to about half of the beam’s wavelength
λ= h/meV = h/[2meE].5 =h/p
Electrons have a larger mass which makes their wavelength very small which allows their amplitude to be less than that of the of atoms they are probing.
At 50keV λ~10-12 m which is less than the width of an atom hence achieving the desired subatomic resolution. This is the theoretical limit of TEM although because of error it is not likely to be achieved.
Basic TEM components
This is synonymous to a normal microscope but with electrons. There are four parts.
There is the energy source (a tungsten filament and Wheinfield Cap) which goes through a lens system (electromagnets focus and accelerate electrons), a sample holder (a grating with amorphous carbon, then an imaging system (lenses and an imaging plate)
TEM electron source
The source contains a cathode of tungsten (negative) and a donut shaped anode (positive). The tungsten is heated to create surface charge, which is confined on a smaller radius cap.
A defocused electron beam is created by creating a several tens of thousands or hundreds of thousands difference in eV across the gap.
The anode is donut shaped in order to prevent electrons at weird trajectories from passing through. This first beam is also passed through the objective aperature to help “pre-size” the beam
TEM lens
This is a three-step process.
First the sample goes through an objective aperture (holes in metal) which helps to define the beam width (smaller=better resolution but lower intensity)
It then travels through a circular EMR which generates a precise magnetic field. This is the objective lens.
Before interacting with the sample it goes through a condenser aperture which is thin (2-100 microns) and removes electrons of a low energy and helps ensure that the probe is monochromatic.
TEM sample stage
The TEM sample stage is characteristically a copper plate with small apertures (~1 micron) and topped with an amorphous (no signal) carbon sheet. This whole setup is usually about 2-3 mm in diameter
TEM imaging system
The TEM imaging system has a set of three EM lenses, two apertures, and a screen.
The first lens (objective) focuses on transmitted and diffracted light to be filtered by the back plate (see bright vs. dark imaging). It then passes through the SA aperture for stray rays and is refocused and projected by the intermediate and projection lenses.
This projects an image on a phosphorescent plate which forms an image similar to film.
TEM Imaging methods
The TEM sample is extremely thin (100’s of nm max) which means that the electron beam propagates through the sample. There are two potential ways that the light can interact. It can be transmitted directly through the sample (bright field imaging) or diffracted by crystal planes which occur in reference to braggs law
The two beams (diffracted and transmitted) have different trajectories, and this is used to filter the beams based on location using the aperture below this is the back plate aperature.
Abberation
This is a term that refers to how light can never be perfectly focused to a single point but instead to the minimum disc of confusion.
spherical aberration is when a collinear electron ray being focused within an EM is not within a homogenous field resulting in different deflection and a finite disc. The field tends to be strongest near the edges of the coil and weaker in the center.
chromatic aberration is due to the fact that different energies of waves will interact with material differently (Snell’s law) thus there is non-equal deflection because of differences in energy. In terms of electrons, the difference in energy levels changes their velocity and hence changes the lorentz force.
Lorentz force
This is the basic force which drive EM focusing of electron beams
F = q V X B
Back focal plane
This is the aperture right below the objective lens (after the beam has gone through the TEM sample which filters out the diffracted and transmitted rays based on their position.
Bright field imaging
This refers to light that is transmitted through a sample without being refracted by the sample. Hence brighter areas are areas where there is less in the pathway of the incident beam aka smaller atoms and/or thinner samples. It is considered a low-resolution imaging method (~nanoparticle resolution)
It produces simple 2D images/projections
Dark field imaging
This refers to imaging using only the diffracted rays. Crucially it is not taking the diffraction pattern of the sample but instead imaging the diffracted rays in 2D so using this mode you can see where your sample has crystalline domains, where strain has altered structures, and the regularity of the crystallinity. By changing the parameters of the incident beam you can identify different characteristics of the sample you are probing.
Phase Contrast Imaging
This is the “high resolution” mode of TEM which involves using a large aperture which enables both the transmitted and diffracted waves through after interacting with the specimen. It produces complex diffraction patterns which require modelling and expertise to understand and uses fourier transforms to understand the resultant wave-pattern.
When done correctly it has sub-atomic resolution.
What impacts high resolution TEM?
Principally, it is a function of thickness of the sample (thicker = more retardation = different phases upon exiting), localized sample density, the focus of the incident rays (changes theta and lambda), scattering of incident electrons, orientation of the sample, and anstigmatism (abberation)
These influences are non-unique to TEM as a normal microscope and XRD are influenced by similar factors.
The top two influences are the beam focus and sample thickness
How does a HREM image work in principle?
Upon exiting the sample, the transmitted waves exit in the same trajectory that they entered whereas the diffracted waves exit at an angle. Where these interfere constructively (where the lines cross) can help to indicate the structure of the material being inspected. The crystalline specimen can then be reoriented to gather all of the rays that satisfy bragg’s equation.
It produces a pattern very similar to the Laue Method

TEM compositional analysis
A TEM will also often have an EDS apparatus. This is really a scintillation counter usually made of SiLi which measures the intensity and wavelength of the incident x-rays which are produced because of the ejection of core electrons via inelastic collisions
Each atom has characteristic x-rays which can be used to identify the composition of the material being scanned to produce a compositional ratio of ~1% error. This is because you can use the different wavelengths of x-rays to provide multiple constraints onto the potential composition of the sample being probed.
Disadvantages of TEM
Primarily this is sample preparation which requires it’s own specialized equipment, is time consuming, and destructive.
TEM can also be destructive to the sample because it is bombarding it with electrons at high energies.
How to prepare TEM samples?
TEM samples must be 10-500 nm thick to allow electrons through (based on composition where larger atoms=thinner)
ultramicroscopy is where a 1mm3 block of sample is put in resin and then sliced using a glass or knife blade. If the sample under inspection is biological in nature then it is usually in liquid nitrogen before being sliced. It then floats on water and is picked up for scanning. If it is still too thick it is AR laser milled.
FIB: is also used to machine an ultra-thin sample for scanning by creating two holes in the sample and leaving a thin strip which is then “glued” using Pt for transport and scanning
FIB instrumentation
A focused ion beam is produced by having a gallium reservoir and a tungsten needle tip. The tip is charged and an external plate is charged with an opposite charge. This attracts Ga2+ ions out of the tip that can then be accelerated and used for milling.
These are always accompanied by an SEM in order to image the resultant milled product and the ions can be used to image objects too because of how collisions depend upon topology and composition
TEM applications in biology
TEM is a good tool for biologists to be able to probe very small things like viruses which have distinctive structures and configurations. It can also be used for imaging the developping products in nanomedicene like fluorescent tags to ensure that they are of ideal parameters.
Scanning Transmission Electron Microscopy (STEM)
STEM is fundamentally TEM but it includes “scan coils” which orient the beam as a raster scanner. It produces a directly interpretable z-contrast image meaning that the contrast of the resultant image reflects the atomic number of the scanned atom. The scanning coils are 4 xy EM coils that bend the beam as needed to raster scan the sample under inspection.
Low-Voltage TEM
LVTEM is a tool that is commonly used in biological imaging. It uses a lower voltage near ~5 keV. This reduces its resolution to ~2-3 nm and requires thinner samples but it protects biological samples and works well for low z atoms (like carbon and nitrogen) by providing higher contrast.
Scanning Electron Microscope: Instrument
This is a tool primarily used for imaging with physical characteristics very similar to a TEM (source and EM lenses in a vaccum) except it has 4 scanning coils and a stage instead of a sample holder because electrons are not transmitted through the sample. It also has lower voltage than a typical TEM (~40keV vs. 100+ keV)
They are used for imaging which is done with a secondary electron detector and a backscatter electron detector. Occasionally there will be an Auger detector for very surficial auger electrons.
Advantages/Disadvantages of SEM
PRO: It is versatile with a magnification capacity that ranges from 10 to 500,000X magnification and a resolution of ~2 nm. There is minimal sample prep (if non-conductive deposit a thin film of metal to stop charge accumulation) and has a high depth of field meaning that the images it produces can appear 3D
CON: High vacuum needed for e beam minimizes the ability to scan hydrated samples (see Nature SEM). No Structure or atomic resolution
Thermionic emission source
This is the “electron gun” in both SEM and TEM. It is composed of three parts.
The filament is tungsten or LaB6 and is needed to be able to withstand the high heat that is created when running high current through the material. Only refractory metals can be used. The tip of the filament accumulates charge (when Ethermal>Eg) and free electrons are drawn out of the material towards the donut-shaped anode.
The Wehnelt cap refers to a cone-shaped cap which has a slight negative charge. This helps to prevent electrons from randomly scattering by repelling them towards a finite point.
EM lenses for electrons
These are simply coils of copper which use Lorentz force (F=-q V X B) to focus ions moving through the coil similar to an optical lens. Because the magnetic field is inhomogneous (weak at the center) the electrons are pushed towards a point of convergence. Electrons moving through the coil are actually spiralling because of the nature of crossing vectors.
Scanning coils
These are tools used within SEM and TEM. They are 4 EM coils that produce heterogeneous magnetic fields used to influence the trajectory of the electron beam. They alter the x-y orientation of the Lorentz force.
Electron beam interaction volume
Because electrons have a large amount of energy, they produce signals from a ~5 micron deep tear-drop shaped volume of material. The signals from each part differ and the higher energy the signal, the deeper it can originate.
At the very upper layer of atoms is auger electrons followed by secondary electrons (~.5 microns) and backscattered e (~2.5 e). The deepest useful information comes from the characteristic x-rays down to a depth of ~4 microns.
Beyond this there are continuum and fluorescent x-rays that are the result of random interactions and provide no useful information.
This is significant because this means that the depth at which you are collecting information from your solid varies based on the information source.
Secondary Electron Imaging
These are lower energy electrons emitted from inelastic scattering. They are ejected from the k-orbitals (n=3). Because of their low energy they only are produced from the uppermost nanometers.
Backscatter electrons
These are high-energy electrons which are reflected aka backscattered through elastic collisions deeper in the material. They have a penetration depth of ~1-2 microns.
Everhart-Thornley Detector
This is the detector used for secondary electrons. It is a cone with a slightly positive potential (~200 V) which attracts the low energy electrons. These are then attracted to an internal scintillation counter (~10k V) which relays a signal to a normal photomultiplier tube to create the computer output.
Backscatter Detector
This is a donut-shaped detector that sits above the specimen to measure the relatively random reflected electrons. They are semiconductors with a scintillation coating which are used to convert the incident electrons into measurable signals.
SEM imaging
The image in an SEM is produced through raster scanning the surface like within AFM or STM. The reported image is like the cathode ray tubes of old black and white tvs where the intensity is a result of the intensity of the emitted electron beam at that particular part of the sample’s surface.
Diffraction Pattern Imaging
This is a form of imaging in TEM synonymous to XRD where you are imaging the diffraction pattern of a substance to identify it’s structure.
Interpretting phase contrast images
When doing phase contrast imaging to understand the true 3D structure requires expert modelling but on a high level if there are very finite discs then the sample is crystalline, if there are blobs then it is a glass, and if there are dots inside of the discs than it is a glass ceramic.
FIB Imaging
This is similar to SEM or TEM where incident ions can backscatter, launch secondary ions, and produces x-rays.
The cascading collisions of FIB go down to ~50 nm/
Field Emission SEM
This is basically a way to do low-voltage SEM with higher resolution and brightness. It does not require a conductive coating and the low voltage prevents sample damage but requires an ultra-high vaccum and has poor BSE results.
It works by having a very sharp convex tip that produces a smaller diameter beam.
How does SEM image topography?
Basically the number of electrons that are able to reach the surface of a material is a function of the travel distance between the collision and the surface. A greater thickness = less electrons.
This is called the edge effect where many electrons escape on the edges of surfaces where relief is high. It is primarily relevant for secondary electrons.
How does SEM image using BSE?
Backscatter images are produced via reflection where the higher the z of the atom it is interfacing with the more reflection occurs. Hence BSE images are proportional to the composition of the surface being scanned.
Topography can be inferred through shadow-based imaging methods which means that you only detect BSE from one side of the sample effectively “illuminating” one side of the sample. This is done by turning off part of the light pipe detector donut.
Depth of field
This is a term that refers to how much distance along the beam’s centerline can be imaged with some minimum resolution. Greater depth of field enables greater “3d-ness” of images.
Generally a larger aperature and shorter working distance decreases the depth of field.
What is the trade-off for greater depth of field?
Usually a greater depth of field is generated by longer working distances or smaller apertures. In both cases this reduces the intensity of the beam which can impact the quality of the image
Resolution and depth of field also have an inverse relationship meaning that as depth of field increases your resolution decreases (depth of field is defined by a beam waist, increasing depth of field if the beam is constant increases the beam waist)
SEM depth of field character
Small wavelength of electrons and small aperature (requiring high intensity beams) enables SEM to have relatively unparalleled depth of field. This is what creates the many cool 3D-esque images.
SEM sample prep
If samples are conductive then there is ~0 sample prep if it is the correct size
If insulative then it will collect charge which create artificial ejections of electrons in cracks and sharp areas producing image artifacts. To combat this, a thin film of C, Cr, Au-Pd, or another conductive metal is deposited onto the sample via sputtering
Sputtering
This is the process of create a metallic plasma that is deposited onto samples as a thin film of a few nanometers. It is particularly useful when needing to develop a conductive surface for something like SEM or for a Si(Li) detector.
Nature SEM
This is a relatively new technology that enables hydrated samples to be imaged using SEM. It has a series of vaccums with a differential pumping mechanism that enables the high vaccum near the electron gun which goes to a few hundred pascals where the sample is.
It produces the same resolution as SEM.
At what pressure does liquid water evaporate?
609 Pa. This is the minimum pressure in a probing enviroment if planning to probe hydrated samples (biological)
What do characteristic x-rays result from?
These result from the inelastic scattering of incident core (K-shell) electrons. This means that the electrons from the n=1 orbital or ejected and electrons from higher orbitals (L,M,O…) drop down in energy to fill the vacancy. This change in potential results in characteristic x-rays.
From what depth to characteristic x-rays result?
Characteristic x-rays can come from depths of up to ~5 microns within the sample. This is relatively deep compared to BSE and SE and means that EDS is not useful for nano-films where composition needs to be analyzed through alternative means.
Emission of Families of X-rays
If an element is present in a sample, all characteristic x-rays are emitted and should be detected simultaneously. Families of x-rays can include ten or more depending upon the specific level and sub-level. These are limited by some quantum selection rules.
The relative intensity of different peak energies is also characteristic to specific elements and this can be predicted through modelling the atoms being probed.
Why does EDS have width in the peaks?
Each peak really has a forest of tiny peaks related to each level and sub-level. The difference in energy is too small to be able to detect though and the peak is recognized as one big blob.
Moseley’s Law
λ = B/(z-C)2
λ α 1/z2
E α z2
Meaning of Moseley’s Law
Moseley’s Law describes the wavelength of characteristic x-rays as a function of the atomic number of the element being probed. It says that energy increases as the square of the atomic number. This means that there is a rapid increase in energy as atomic number increases which makes sense because as atomic number increases the electronic attraction between electrons and the nucleas would increase significantly.
What are the three main ways that x-rays can be produced in EDS?
- electrons can eject an electron (preferred) and cause a cascade from the upper orbitals which releases characteristic x-rays.
- The electron can interact with (be decelerated by) the strong positive nucleus and the deceleration can emit an x-ray. These are the continuum x-rays.
- the incident electron can emit an x-ray from any of the above which then triggers a high orbital electron to be ejected and when the hole is filled a low-energy fluorescent x-ray is emitted.
Brehmsstrahlung Continuum
This is the hump-shaped continuum of x-rays produced during EDS from incident electrons being significantly decelerated by the positive nucleas.
It reveals no specific information about the material being probed and data must be manipulated to remove the influence of continuum x-rays. This occurs through either subtracting the average x-ray intensity (if in the tail region) or modelling the continuum (if in the hump region)
It must be removed before interpreting spectra because to interpret spectra, you must integrate the peaks (to find proportions based on energy) and thus each of the true peaks needs to be separated from background intensities.
Ways to remove the continuum x-rays
- Background averaging: This is best for when the continuum is relatively constant and an average relative intensity is constant or linear. The area below this average is integrated and subtracted from the spectra.
- Background simulation: This is best at low energies when the continuum is non-linear. In this situation, you must take a moving-average model to integrate and subtract from the peak.
What are the components of an EDS detector?
This is functionally a tiny tube that sits near the SEM or TEM surface (to collect x-rays directly from the scanned surface). It includes a collimator which limits the collection angle and prevents random x-rays from BSE’s from entering the detector. Behind this is an electron trap which traps any BSE’s with a slightly positive voltage. Then there is a window to maintain a vaccum for the detector. This is followed by the Si(Li) crystal and FET preamplifier.
This is all kept at the temperature of liquid nitrogen and routes signal to the amplifier (a bunch of computer stuff)
EDS detector entrance window
Design constraints for the window include that it must be able to be transparent to x-rays but also be rigid enough to hold a vaccum.
Be Windows are the windows that are used in x-ray tubes. They are rigid and strong but are only transparent to rays with E>1 keV
Polymer Windows are very fragile and require a support grid but are transparent down to ~100 eV which is good for low atomic number elements down to Be or B
Si(Li) detector
This is a common detector used to measure the energy of x-rays. It is usually about 3 mm thick with Au contacts on both sides which have a voltage applied to them. Then there is a “dead layer” of Li doped Si on both ends that is about 100 nm thick. This is there to prevent hole migration to the anodes. The middle is all Si.
The purpose of the detector is to cause an “avalanche” of hole-electron pairs that creates electron drift and a related current that can be detected and used for analysis. Hole-pairs are produced at 3.8 eV because of quantum mechanics even though Si has an Eg of 1.1 eV
FET-Preamplifier
The FET-preamplifier is a p-n junction where there is a semicircular “block” of transistor material. A working current is applied to the n parts of the preamplifier and the p part is attached to the Si(Li) detector. This feeds weak current into the p part of the transistor and provides energy for current to hop through the insulative material. This effectively converts the weak signal into a step up of voltage that can be precisely and quickly monitored.
EDS Detector: Main Amplifier
This is a computer which converts the staircase signals from the preamplifier into individual voltage pulses where the amplitude of the pulse is proportional to the energy of the incident x-ray. This is also the first component outside of the tube,
Pulse Pileup
This refers to when voltage pulses have very little to no gap between consecutive pulses. This causes an overlap of pulses and a falsely intense amplitude reading. This is mitigated by increasing the count rate of the amplifier and also ommitting pulses that begin to increase again before reaching 0 voltage
Multichannel Analyzer (MCA)
This is a computer that converts analog pulse signals into digitized signals. It basically measures the amplitude of the pulse voltage and uses it to place it into one of 1024 bins/channels. Each bin/channel covers 10 ev. It then sends these to the computer’s memory unit to be displayed as counts vs energy meaning that the energy of the incident wave is proportional to the peak position wheras the # of counts in the signal channel is proportional to peak intensity
EDS Detector efficiency
The Si(Li) detector is only efficient between ~.5-20 keV although x-rays can be several tens of thousands of keV’s. This means that we are limited in our ability to detect x-rays and that the intensity of peaks is not fully independent of their wavelength or in other words, peak wavelength influences the ability to detect the x-ray.
At x-rays with energies exceeding 30keV the x-ray will propagate through the Si(Li) detector without donating all of its energy producing an inaccurate signal.
EDS Si(Li) Artifacts
- Escape peak: This refers to a peak that is ~1.74 keV less than the main peak. It results from silicon absorbing 1.74 keV (the energy needed to change electronic levels).
- Sum Peaks: This is the result of pulse pileup where an additional x-ray hits the Si(Li) detector before it is finished processing the one prior. It can result in either an excess intensity of the second photon or it can produce an artificial peak at an energy equal to ~twice the incident ray.
- Spurious x-rays: this refers to x-rays that result from backscattered electrons (high energy) interacting with the instrument below and emitting x-rays that are not from the specified collection window.
The probability of two photons arriving at the same time (pulse pileup) is proportional to what?
It is proportional to intensity squared so a decrease in incident intensity leads to a rapid decrease in the intensity of the pulse pileup or sum peak.
Why are spurious x-rays particularly difficult?
Spurious x-rays are legitimate signals, but they are not representative of the spot which you want to analyze.
While an x-ray indicating that your lower aperture material is in your sample can be predicted, if the BSE reflects off of the aperture and re-interacts with the sample in a different location it can release an x-ray that is difficult to recognize as an artifact. This is most common within TEM.
How to minimize spurious x-rays?
Coat the inside of the EDS/SEM/TEM with a low Z element. The probability of backscatter decreases as Z decreases, hence reducing Z decreases the P(backscatter).
EDS Precision (Detection limit and spatial resolution)
EDS is best for bulk analyses although, in theory, it can have a .1 wt% (1000 ppm) detection limit. This is dependent on the Quality of the standard, quality of data analysis, and presence of artifacts. It is calculated by integrating the number of counts vs. E to find the proportional amount of energy released by each peak and matching it to models.
The spatial resolution is constrained by the density of the solid and the maximum interaction volume diameter. Higher density and thin samples minimize spread and increase spatial resolution. In most samples, the best spatial resolution is ~2 microns.
How is cell parameter related to d spacing in a cubic cell?
a0 = d/[h2 +k2 +l2].5 where ao = the cell length (all are equal because it is a cube. d = d-spacing and h,k,l are the miller indices.
What types of images are produced with NSOM?
These are typically topologic images that are mapped with different optical properties like refractive index.
What are beta filters and why are they useful?
When conducting XRD we need to have a monochromatic source (interference is dependent upon incident wavelength via Bragg’s law). Hence, if our source produces two wavelengths (K-alpha and K-beta where K-alpha is ~10* more intense) then we need to filter out the less intense wavelength (K-beta) This is done with materials of a slightly lower atomic number than the source material with a limitted impact on the intensity of k-alpha.
Moire Fringes
This is an image artifact which can occur during HRTEM when there are multiple structures superimposed on one another where the two patterns overlap and create a third pattern that is not reflecting the true nature of the specimen. It can occur when you are not in focus. It shows the complexity of HRTEM which requires modelling but is able to have atomic resolution.
Wavelength Dispersive Spectroscopy Concept
This is a technique that mirrors normal spectroscopy, but it is for x-rays. It has higher precision than EDS through using a diffractive monochromator (crystal with known d-spacing) rather than an energy (Si(Li)) detector like is used within EDS. By directly measuring the wavelength of x-rays there is a greater precision.
It consists of an electron beam, sample holder, analyzing crystal, and x-ray detector (tube with gas that is ionized by x-rays)
It has a spatial resolution similar to that of EDS (~1 micron)
How is wavelength scanned in WDS?
In WDS the analyzing crystal, x-ray detector, and sample all sit on the Rowland Circle. The analyzing crystal has a known structure which is used to understand the d-spacing based on orientation and only constructively diffract specific wavelengths.
By rotating the analyzing crystal, different d-spacings are revealed. These basically act as a monochromator based on the specific crystal orientation.
Because the range of directionality is limited, the wavelengths that are available to be scanned is limited. Hence, to scan the full spectrum, several crystals (with different d-spacings) are needed to cover all relevant wavelengths.
Common analyzing crystals in WDS
The three most common analyzing crystals, in order from highest to lowest energy are:
Lithium fluoride (LIF), Pentaerythritol (PET), and Thallium acid Phthalate (TAP)
These three crystals provide x-ray wavelengths from Z=8 (O) to Z=92 (U) with significant overlap between wavelength ranges. This is important because it means that you can match up the produced spectras when using the three crystals to gather the full spectrum.
Analyzing crystals: What is the relationship between 2d and wavelength range?
As the 2d of the crystal increases the wavelength of x-rays they diffract increases. This makes sense in Bragg’s law because lambda is directly related to d. This also means that the larger the d-spacing the lower the energy that the crystal diffracts.
Analyzing crystals must have a d-spacing of ~1 angstrom to match the incident x-rays in order for diffraction to occur via braggs law.
Take-off angle and Rowland Circle
The take off angle is the angle between the sample and the analyzing crystal (usually 40o). It remains constant during the scanning process. The Rowland Circle is the circle where the crystal, detector and sample lay. When analyzing the range of wavelengths only the incident angle between the ray and the analyzing crystal and phi in Bragg’s equation changes.
Types of WDS crystal design?
For optimal efficiency (minimal absorption) the analyzing crystal must be bent so that it’s surface is on the Rowland circle.
johan optics is where the analyzing crystal is bent to 2R of the Rowland Circle. This results in some broadening and asymmetry of the focusing “point”
johansson optics is where the crystal is bent and then hollowed in order to perfectly fit the rowland circle and it results in proper focusing over the whole range of angles.
WDS x-ray detectors
There are two types of detectors. gas flow and sealed.
They are principally the same, x-rays ionize an otherwise inert gas (Ar) and create electron-hole pairs. These are accelerated towards the detector wall (-) and detector wire (+) which creates an avalanche of such interactions.
They are constructed as a tube with beryllium windows and ~1-2 kV
What is the average number of electron-ion pairs in an x-ray detector?
n=E/ei
Where: E=incident x-ray energy (eV), ei = effective ionization potential of the detector gas (eV).
n is the average number of pairs produced. It is not large which is why the avalanching is important.
WDS configuration: Electron microprobe
These are box-like attachments that are on SEM’s. There can be up to 5 of them for one SEM (each with two crystals). This increases the analytical flexibility. There is usually an everhart-thornley detector attached to image the topography of the area.
In practice, a standard of known composition is measured very close to each of the samples to verify/confirm results.
Detection parameters for an electron microprobe
You analyze each element independently (each ~4 minutes of analysis) yielding a minimum detection limit of 100-300 ppm.
The minimum detection (theory) is .01 wt % (5 ppm)
The spatial resolution is ~1 micron under normal conditions.
What influences detection in WDS
Minimum detection limits are dependent on the electron beam and the counting times for the analysis.
Generally, the lighter the element the longer the counting time and the less precision of analysis. To reach very low (5 ppm) detection the samples must be able to resist high voltages/intensities, currents, and counting times.
LEAP/APT/ 3D atom probe capabilities
LEAP=Local Electrode Atom Probe APT = Atom-Probe Tomography
This technology is able to 3D image, determine chemical composition, and measure at an atomic scale (~.1-.3 nm resolution in depth and .3-.5 nm laterally). It uses a pointed sample to accelerate ions towards an imaging detector and measures travel time to determine the mass.
The time-of-flight (TOF) is proportional to mass over charge which is used for composition and detailed atomic reconstruction of the tip is used for topography.
How does APT work?
The sample is prepared as a sharp tip. A high voltage (5-20 kV) is applied so the tip has tens of V per nm. This induces the evaporation of ions at the sample tip which are accelerated towards the detector.
A laser or voltage pulse “free” said electrons and the time of flight reflects their journey from the tip to the detector. This must occur within an ultra high vacuum in order for the atoms to not collide with gas molecules.
Kinetic energy is equal to what for the mass analysis?
.5mv2 = qV
This is used to accelerate the ions to a specific KE after being evaporated from the sample tip.
TOF
time of flight is the time it takes between the laser pulse and the ion reaching the detector interface. The only unknown in the equation below is m/q which is solved for by finding t
t=[d2m/2qV].5 where t = TOF
q=charge
V=voltage potential
d= travel distance
APT detection
APT detection occurs as a position sensitive detector TOF mass analyzer which does 2D imaging.
It has two microchannel plates (plates of tiny tubes ~10 microns in diameter). The ions enter the tubes and collide with the edges to create a cascade of electrons which are detected by an anode.
The TOF is recorded for m/q and the position is recorded to reconstruct the sample tip based on the results of the sensing.
In EDS how would you check if sum peaks or escape peaks exist?
You would decrease the intensity of the beam because the peak intensity is proportional to I2. If your sample is sturdy you can decrease the intensity of the electron beam by reducing the filament current and increase the count time to receive a similar signal:noise ratio
how does LEAP release atoms at the tip?
The sample is highly charged using DC current (~10-20kV) which makes extremely high charge density at the tip. This is dependent upon the sample and needs to be experimented with before accurate data collection.
The atoms in the outermost layer are then further pushed using either a laser or a high voltage pulse. This gives the outermost atoms slightly more energy than their bonding energy and frees them from the solid state and accelerates them towards the local electrode giving them the KE that is measured by the PSD.
WDS: issues with braggs law
In WDS because you are directly measuring constructive interference via diffraction you also must account for the higher orders of diffraction although their signals are significantly less.
Difference between LEAP and APT
LEAP has a conical electrode a few microns (~10) from the sample tip. This significantly enhances the collection rate (103 to 106 atoms/minute) and the resolution of the instrument. This also increases the field of view by a factor of 50 (~200 nm2 to ~10k nm2) by having electrons travel at an angle from the sample tip to the PSD.
LEAP in laser pulse mode
When in laser pulse mode LEAP uses a high power laser focused on a very tight spot. This is usually a UV laser. High throughput is achieved by having pulse frequencies as high as 1 MHz and large field of view is achieved because of the ability to have the laser interact with a large portion of the sample tip.
The main detraction of this method is that there is additional equipment that must be purchased and the calibration of the laser so that it is directly on the sample tip is difficult.
LEAP in HV pulse mode
This mode sends a HV pulse (~.5-15 kV dependent on material) to free the electrons at the sample tip. The pulse duration is ~12 ps and occurs at a rate of 2- 200 kHz. It is slower than laser mode and has a smaller field of view. That said, it has less equipment and less alignment.
LEAP sample tip fabrication process
First you use a FIB to mill out a tiny chunk of sample that gets mounted onto an Si micro-post (~2 microns in diameter) using platinum. Then you use the FIB to carve the sample until it is a point.
This should be positioned along the boundary edge or where you want to image.
What constraints are used in EDS to determine composition?
The energy and intensity of many characteristic peaks provides multiple constraints to the sample that is being imaged. When putting this in the context of many known compositional fingerprints it enables the systems to basically solve a series of equations to arrive at an answer.
What are the four main steps that occur when an x-ray encounters and EDS detector?
- ) Si(Li) detector has an avalanche of electron-hole pairs
- This is detected on the FET preamplifier as a voltage step-up
- Next, the main amplifier converts the step-up to a voltage pulse.
- The multi-channel analyzer converts the pulse into a digital signal (with some intensity) and then places it in a “bin” which can be interpreted as a histogram for integrating.
What are the element limits on WDS?
WDS can measure elements between oxygen (Z=8) and Uranium (Z=92) using the three main amplifying crystals (LIF, PET, and TAP)
What is a typical distance for the flight path of the atom in LEAP/APT?
This is usually over .5 meters. The longer the distance the greater the time of flight and the greater the differentiation between atoms of similar m/q ratios. This is most important when dealing with material with elements of near equal composition.
What is the typical size of a LEAP/APT sample tip?
This is usually ~10-40 nm in diameter and about 200 nm in length. This has ~30*106 atoms inside.
To get this tip you first mill a block out of the sample of interest and then afix it to the Si post. Then you use the FIB and a micromanipulator to mill it to spec.
How is x,y,z of atoms resolved in APT/LEAP?
The x,y position of the atom is given by the position sensitive detector (PSD). The z position is given as a function of time where the sample is evaporated layer by layer over a distinct time interval.


