Significant figures and conversion factors

Question 1

Define accuracy.

Answer 1

How close a measurement is to a true value. Accuracy can only be determined if there is an accepted true value against which to compare.

Question 2

Define precision.

Answer 2

How repeatable a series of measurements are. At one level, therefore, precision requires a set of data of identical measurements. Precision, however, is also estimated from signifcant figures - which give an indication of a probable precision in the event that the measurement is repeated.

Question 3

Define significant figure.

Answer 3

All certain digits plus one estimated digit. “Certain”, in this context, means whether a second measurement would give an identical measurement. This level of “certainty” is directly tied to the precision of the equipment (e.g. graduated cylinder vs pipette) used to make the measurement.

Question 4

Examine the following burette and record to the correct number of significant figures.

Answer 4

The best estimate for this burette measurement is 2.38 or 2.39 mL.

Question 5

Examine the following graduated cylinder and record to the correct number of significant figures.

Answer 5

The best estimate for this graduate cylinder measurement is 76.3 or 76.4 mL.

Question 6

Examine the following graduated (Mohr) pipette and record to the correct number of significant figures.

Answer 6

The best estimate for this pipette measurement is 2.53 or 2.54 mL.

Question 7

Examine the following graduated cylinder and record to the correct number of significant figures.

Answer 7

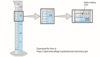
The best estimate for this graduate cylinder measurement is 21.6 or 21.7 mL.

Question 8

Indicate the correct number of significant figures in the following number: 1245.0

Answer 8

1245.0 has five significant figures. The zero after the decimal place is the “estimated” digit.

Question 9

Indicate the correct number of significant figures in the following number: 1024.0

Answer 9

1024.0 has five significant figures. The zero after the decimal place is the “estimated” digit. The zero “trapped” between the 1 and the 2 is a certain value and is part of the measurement.

Question 10

Indicate the correct number of significant figures in the following number: 12450

Answer 10

12450 has four significant figures. The last “tailing” zero is not considered significant. This zero in a sense indicates how large the number is. Using scientific notation, one would write 1.245x104.

Question 11

Indicate the correct number of significant figures in the following number: 1.2450

Answer 11

1.2450 has five signifcant figures. The last zero is the “estimated” digit.

Question 12

Indicate the correct number of significant figures in the following number: 0.001240

Answer 12

0.00124 has three significant figures. The zeros before the “1” indicates how small the number is. Using scientific notation one could write 1.24x10-3.

Question 13

Indicate the correct number of significant figures in the following number: 0.01245

Answer 13

0.01245 has four significant figures. The zeros before the “1” indicates how small the number is. Using scientific notation one could write 1.245x10-3.

Question 14

Indicate the correct number of significant figures in the following number: 1.245x10-3

Answer 14

1.245x10-3 has four significant figures.

Question 15

In adding one number to another, what will determine the number of significant figures in the final answer?

Answer 15

In addition, signifcant figures are determined by looking at the least number of digits past the decimal place.

Question 16

In subtracting one number from another, what will determine the number of significant figures in the final answer?

Answer 16

In subtraction, signifcant figures are determined by looking at the least number of digits past the decimal place.

Question 17

In multiplying one number with another, what will determine the number of significant figures in the final answer?

Answer 17

In multiplication, significant figures are determined by looking at the number with the least number of significant figures.

Question 18

In dividing one number with another, what will determine the number of significant figures in the final answer?

Answer 18

In subtraction, significant figures are determined by looking at the number with the least number of significant figures.

Question 19

What conversion factor is required to convert mass in grams (g) to mass in kilograms (kg)?

Answer 19

To convert mass in grams (g) to mass in kilograms (kg) one needs to multiply by 1 kg/1000g.

Question 20

What conversion factor is required to convert mass in milligrams (mg) to mass in kilograms (kg)?

Answer 20

To convert mass in milligrams (mg) to mass in kilograms (kg) one needs to multiply by 1 kg/1x106 mg.

Question 21

What conversion factor is required to convert mass in kilograms (kg) to mass in grams (g)?

Answer 21

To convert mass in kilograms (kg) to mass in grams (g) one needs to multiply by 1000 g/1 kg.

Question 22

What conversion factor is required to convert mass in kilograms (kg) to mass in milligrams (mg)?

Answer 22

To convert mass in kilograms (kg) to mass in milligrams (mg) one needs to multiply by 1x106 mg/1 kg.

Question 23

What conversion factor is required to convert volume in milliliters (mL) to volume in litres (L)?

Answer 23

To convert volume in milliliters (mL) to volume in liters (L) one needs to multiple by 1 L/1000 mL.

Question 24

What conversion factor is required to convert volume in milliliters (mL) to volume in centilitres (cL)?

Answer 24

To convert volume in milliliters (mL) to volume in centiliters (cL) one needs to multiple by 1 cL/ 10 mL.

Question 25

What conversion factor is required to convert volume in mL to volume in cubic centimetres (cm³)?

Answer 25

To convert volume in mL to volume in cubic centimeters (cm³) one needs to multiple by 1 cm³/ 1 mL.

Question 26

What conversion factor is required to convert area in square (in²) to square feet (ft²)?

Answer 26

To convert area in square (in²) to square feet (ft²) one needs to multiply by (1 ft/12 in)².

Question 27

What conversion factor is required to convert volume in cubic centimetre (cm³) to cubic metres (m³)?

Answer 27

To convert volume in cubic centimeter (cm³) to cubic meters (m³) one needs to multiply by (1 m/100 cm)³.