Sequences and series (SL) Flashcards
What is an arithmetic sequence?
A list of numbers that change by adding or subtracting the same amount each time.
What is a “common difference, d”?
It’s the amount of increase (or decrease when negative) between terms of an arithmetic sequence.
How can you find d when given two consecutive terms (like u3 and u4) of an arithmetic series?
You subtract the terms. Always the later term minus the earlier one.
u4 - u3 = d
How can you find d when given two non-consecutive terms (like u4 and u8) of an arithmetic series?
You set up a system of equations and solve it (with linSolve).
- Write an equation for each un you know.
- Plug these equations into linSolve.
How can you find un if you already know u1 and d of an arithmetic series?
You plug it into the formula from your booklet.
What’s the difference between un and n?
- n* tells you the placement of the term. Like, 1st, 2nd, 37th, etc.
- un* is the actual value of the term.
What’s the difference between un and Sn?
- un* is the value of only the nth term
- Sn* is what you get if you add together all of the n terms.
What are context clues that you should be finding Sn?
You see these words in the question:
- calculate/find the total…
- the sum of the first n terms…
Your formula booklet has two equations for Sn of an arithmetic sequence.
Which one should you use?
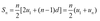
It all comes down to whether you know un or d.
- Use the first one if you only know u1 and d.
- Use the second one if you know both the 1st and last terms (u1 and un).
What is a geometric sequence?
A list of numbers that change by multiplying (or dividing) the same amount each time.
What is a “common ratio, r”?
It’s the multiple of increase (or decrease when a fraction less than 1) between terms of a geometric sequence.
How can you find d when given two consecutive terms (like u3 and u4) of an arithmetic series?
You divide the terms. Always the later term divided by the earlier one.
r = u4 ÷ u3
How can you find r when given two non-consecutive terms (like u4 and u8) of an geometric series?
You set up a system of equations and solve it (with nSolve).
- Write an equation for each un you know.
- Solve one equation for u1 by hand. (It will still have r in it).
- Substitute this equation into the other. (Now there are only rs.)
- Solve this equation with nSolve.
How can you find un if you already know u1 and r of a geometric series?
You plug it into the formula from your booklet.
Your formula booklet has two equations for Sn of a geometric sequence.
Which one should you use?
It literally makes no difference. Some people argue that one is better than the other, depending on whether r is greater or less than 1. But this is nonsense. Use either one; it doesn’t matter at all.
What type of sequence (arithmetic or geometric) is it if you are asked about simple interest?
Arithmetic!
If the question talks about “percent increase” or “percent decrease”, what type of sequence is it?
Geometric!
r = 1 + “percent increase”
r = 1 - “percent decrease”
How can you tell when a series exceeds some value?
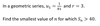
You set up an equation for when Sn equals that value.
Nsolve to find n.
If n is a decimal number, check Sn for the integer values above and below the decimal number.
