Semester 1: Questions Flashcards
Define thermodynamics
Relations between macroscopic quantities, such as heat and other forms of energy, without understanding the statistical origin.
Define statistical physics
The explanation of thermodynamic laws, requiring the use of thermodynamic relationships in order to explain the physics.
Define vulcanisation
The curing of elastomers, such as latex, into solid rubber.
What is a system?
Whatever part of the universe we choose to study.

What is the surrounding?
Parts of the universe that are not chosen to study.
What is a phase?
A region within a system that is homogeneous and has well defined boundaries.

What is a closed system?
When there is no particle exchange between the system and surroundings.
What is an adiathermal system?
No heat exchange allowed between the system and surrounding (a thermally isolated system).
What is an adiabatic system?
An adiathermal and reversible system (often used synonymously with adiathermal).
Define isothermal
A constant temperature.
Define isobaric
A constant pressure.
Define isovolumic
A constant volume.
Define equilibrium
A state without apparent change. For example, a cease of heat flow refers to thermal equilibrium and fixed boundaries refers to mechanical equilibrium. Equilibrium allows functions of state to be defined.
What is a function of state?
Any quantity that has a well defined value for each equilibrium state (not including microscopic quantities such as particle velocity). In thermodynamics these are often referred to as thermodynamic functions, thermodynamic coordinates, or thermodynamic variables.
What is an extensive function of state (with examples)?
A function of state that is proportional to the system size. Examples: energy, volume, and magnetisation.
What is an intensive function of state (with examples)?
A function of state that is independent of the size of the system. Examples: temperature, pressure, and magnetic field.
Are microscopic quantities functions of state? Why?
They aren’t because they vary even when the system is in equilibrium.
Give two examples of properties that aren’t functions of state. Why aren’t they functions of state?
- Work done
- Heat transferred
These properties depend on the process that causes the energy transfer as well as the states involved.
Define the zero-th law of thermodynamics
Two systems in thermal equilibrium with a third are also in thermal equilibrium with each other.
What is the equation that relates temperature in Fahrenheit to temperature in Celsius?
F = temperature in Fahrenheit
C = temperature in Celsius

What is a thermometer?
An instrument for measuring and indicating temperature, typically designed based on thermal expansion.
Who developed the 3 types of thermometers?
- Galileo Galilei
- Daniel Gabriel Fahrenheit
- Anders Celsius
How does the Galilei thermometer work?
Air is trapped in a cylinder that floats or sinks in liquid depending on its temperature.
How does the Fahrenheit thermometer work?
It is a refined version of the Galilei thermometer that uses glass tubes and the Fahrenheit temperature scale.
How does the Celsius thermometer work?
Modern thermometers use this model, where the temperature scale is decimalised with 0ºC being the freezing point of water and 100ºC being the boiling point.
What is the ideal gas equation?
p = pressure
V = volume
n = number of moles
R = gas constant
T = temperature

What is the equation that relates temperature in Kelvin to temperature in Celsius?
K = Kelvin
ºC = Celsius

What is an equation of state?
An equation that relates different thermodynamic functions to one another. These are generally given the notation f(p, V, T, …).
What are degrees of freedom?
The number of independent parameters that define the state of a system.
What is redundancy?
The statistical effect of having more functions of state than independent variables; it occurs due to the existence of equations of state.
What is the form of a partial derivative for x = x(y, z)?

What is the equation for the reciprocal theorem?

How can the reciprocal theorem be derived?
1) Calculate the partial differentials of two equations x = x(y, z) and z = z(x, y).
2) Substitute the partial differential of z = z(x, y) into that of x = x(y, z).
3) The coefficients of dx must be equal to 1 and those for dy must be equal to 0 so the dx coefficients can be rearranged to find the reciprocal theorem.
What is the equation for the reciprocity theorem?

How can the reciprocity theorem be derived?
1) Calculate the partial differentials of two equations x = x(y, z) and z = z(x, y).
2) Substitute the partial differential of z = z(x, y) into that of x = x(y, z).
3) The coefficients of dx must be equal to 1 and those for dy must be equal to 0 so the dy coefficients can be rearranged to find the reciprocity theorem.
A differential is exact if it is ______ and _____ ______ everywhere.
Finite
Single valued
What equation can be used to prove that a function, f = f(y, z), is single-valued?
Given that df = Y(y, z)dy + Z(y, z)dz, the following must be true:

All functions of state are _____ ______ so have exact differentials.
Single valued
Define the first law of thermodynamics
Energy is conserved if heat is taken into account.
How can the first law of thermodynamics be expressed mathematically?
∆E = sum of work done on the system
∆W = work done to the system
∆Q = heat supplied to the system

Define heat supplied to a system
The energy entering a system through means other than work done, represented by the symbol ∆Q.
What is the equation for the first law of thermodynamics when changes are infinitesimal?
dE = đW + đQ = -pđV + đQ
đW = -pdV = mechanical work done
đQ = heat supplied
Define heat capacity
The heat energy required per unit increase in the temperature of a system.
What is the equation for heat capacity?
C = heat capacity
đQ = change in heat energy
dT = change in temperature

How can the equation for heat capacity be derived?
1) Calculate the exact differential of energy with respect to temperature and volume, given that they are independent.
2) Substitute this into the inexact differential for heat supplied.
3) Divide this differential by the change in temperature to give heat capacity.

Define specific heat capacity
The heat capacity per unit mass of the system, usually represented by the symbol, c. Specific heat capacity has the units J/K/kg.
What is the equation for isovolumic heat capacity?
Cᵥ = isovolumic heat capacity
đQ = change in heat energy
dT, ∂T = change in temperature
∂E = change in energy

What is the equation for isobaric heat capacity?
Cₚ = isobaric heat capacity
đQ = change in heat energy
dT, ∂T = change in temperature
∂E = change in energy
∂V = change in volume
p = pressure

What is the equation for the difference between isobaric and isovolumic heat capacity?
Cᵥ = isovolumic heat capacity
Cₚ = isobaric heat capacity
∂E = change in energy
∂V = change in volume
∂T = change in temperature
p = pressure

What is the adiabatic index?
The ratio between isobaric and isovolumic heat capacities for an ideal gas (as E is only a function of T for an ideal gas).
What is the equation for the adiabatic index?
γ = adiabatic index
Cᵥ = isovolumic heat capacity
Cₚ = isobaric heat capacity
R = gas constant

How can the equation for the adiabatic index be derived?
1) Rewrite the ideal gas equation with the knowledge that the internal energy has no dependence on volume (so ∂V/∂T = R/p).
2) Substitute this into the equation for the difference between isobaric and isovolumic heat capacity.
3) Calculate the ratio between these two heat capacities.
What is the adiabatic index for a monoatomic (or ideal) gas?
Cᵥ = isovolumic heat capacity
Cₚ = isobaric heat capacity

What is the adiabatic index for a diatomic gas?
Cᵥ = isovolumic heat capacity
Cₚ = isobaric heat capacity

What are the two types of expansion of 1 mole of an ideal gas?
- Isothermal expansion
- Adiabatic expansion
Describe isothermal expansion
Isothermal expansion occurs when temperature is constant. From the first law, this menas that heat must be supplied to expand an ideal gas from one volume to another at a fixed temperature.
What is the equation for isothermal expansion?
∆Q = heat supplied
p = pressure
R = gas constant
T = temperature
V₁ = initial volume
V₂ = final volume

Describe adiabatic expansion
Expansion that occurs when no heat is exchanged (so đQ = 0).
What is the equation for adiabatic expansion?
T = temperature
V = volume
p = pressure
γ = adiabatic index

How can the equation for adiabatic expansion be derived?
1) As no heat is exchanged, dE = dW = -pdV from the first law of thermodynamics.
2) For an ideal gas, dE = CᵥdT and pV = RT.
3) Substitute the ideal gas equations into the equation for the first law.
4) Take logs of either side and rearrange.
What is the shape of a p-V plot for adiabats and isotherms?

What is a reversible process?
A process that occurs infinitely slowly so that the system goes through an infinite sequence of equilibrium states (which are infinitely close together). This must occur without friction, turbulence, acceleration, or anything else that results in an imbalance of forces. This is often referred to as a quasistatic process.
What is an irreversible process?
A process that has asymmetry in time due to an imbalance of forces within the system.
Give an example of an irreversible process
Joule expansion

Define joule expansion
The irreversible expansion of gas into a vacuum upon the sudden lifting of a partition. It is irreversible due to the large number of gas molecules.

The ______ law of thermodynamics is the only law in the entirety of Physics/Science that is time-irreversible.
Second
Define the second law of thermodynamics
Heat always moves from hotter objects to colder objects, unless energy is supplied to reverse the direction of heat flow. Hence, the total entropy of a system either increases or remains constant in any spontaneous process; it never decreases.
What is the Kelvin definition of the second law of thermodynamics?
No process is possible whose sole result is the complete conversion of heat into work.
What is the Clausius definition of the second law of thermodynamics?
No process is possible whose sole result is the transfer of heat from a colder to a hotter body.
What is a heat engine?
A system in which a working substance (usually an ideal gas) is used cyclically. It interacts with two heat reservoirs at different temperatures; heat is obtained from the hotter reservoir and work is done to pass some of it to the cooler reservoir.
Given example of a heat engine
The Carnot cycle
Describe the process of the Carnot cycle
A heat engine is formed that consists of 2 isotherms and 2 adiabats. In this engine, reversible processes can occur in this order:
1) Isothermal expansion
2) Adiabatic expansion
3) Isothermal compression
4) Adiabatic compression
How can the total work done in the Carnot cycle be calculated?
By calculating the area enclosed by a p-V graph for 2 isotherms and 2 adiabats.

What is the equation for the work done by a heat engine (using the first law of thermodynamics)?
W = work done by the system
Qₕ = heat absorbed by the system
Qₗ = heat released by the system

What is a heat pump?
A heat engine in reverse. This means that heat is extracted from a lower temperature and delivered to a higher temperature, like a refrigerator.
At what part of the Carnot cycle is work done by the system and heat is absorbed?
Isothermal expansion
At what part of the Carnot cycle is work done by the system and no heat is exchanged?
Adiabatic expansion
At what part of the Carnot cycle is work done on the system and heat is released?
Isothermal compression
At what part of the Carnot cycle is work done on the system and no heat exchanged?
Adiabatic compression
What is the equation for heat absorbed by the system during isothermal expansion in the Carnot cycle?
Qₕ = heat absorbed

What is the equation for the temperature difference during adiabatic expansion in the Carnot cycle?
Tₕ = higher temperature
Tₗ = lower temperature

What is the equation for heat released by the system during isothermal compression in the Carnot cycle?
Qₗ = heat released

What is the equation for the temperature difference during adiabatic compression in the Carnot cycle?
Tₗ = lower temperature
Tₕ = higher temperature

What is the equation for ratio between heat absorbed by the system and heat supplied by the system (using the 4 Carnot cycle equations)?
Qₕ = heat absorbed by system
Qₗ = heat supplied by system
Tₕ = higher temperature
Tₗ = lower temperature

What is the equation for the efficiency of a Carnot engine?
η = efficiency
W = work done
Qₕ = heat absorbed by system

What is the equation for the efficiency of a heat pump (refrigerator)?
η = efficiency
W = work done
Qₗ = heat supplied by system

Describe a Carnot engine (as a diagram)

Describe a Carnot refrigerator (as a diagram)

Define Carnot’s theorem
Of all heat engines working between two given temperatures, none is more efficient than a Carnot engine.
How can Carnot’s theory be proven?
By contradiction. Suppose there was an engine more efficient than the Carnot engine; this engine could be used to drive the Carnot engine in reverse so the net effect would be to transfer an amount of heat from cold to hot. This violates Clausius’ statement of the second law.
Define the corollary of Carnot’s theorem
All reversible engines have the same efficiency as that of a Carnot engine.
How can the corollary of Carnot’s theorem be proven?
By contradiction. Suppose there was a reversible engine less efficient than the Carnot engine; the Carnot engine could be used to drive this engine in reverse so the net effect would be to transfer an amount of heat from cold to hot. This violates Clausius’ statement of the second law.
What does Carnot’s theorem prove?
It proves that the Kelvin statement and the Clausius statement of the second law of thermodynamics are equivalent.
What is thermodynamic temperature?
A definition of temperature that is not dependent on any material property. Instead it used reference temperature and compares the amount of heat exchanged.
How is thermodynamic temperature defined using heat engines?
1) Pick a reference temperature, x₁.
2) Measure another temperature, x₂, by running a reversible heat engine between the two temperatures and comparing the amount of heat exchanged: x₂ = x₁ * Q₂/Q₁.
What is Maxwell’s Demon?
A thought experiment in which a hypothetical intelligent being is capable of detecting and reacting to the motion of every individual molecule in a system. For Joule expansion, this ‘demon’ could control the partition so that only high energy molecules can pass through the partition and low energy molecules remain on the original side. This would raise the temperature in the high energy chamber and lower it in the low energy chamber which is a violation of the second law of thermodynamics.
Define entropy
A thermodynamic quantity/function of thermodynamic variables that measures how much of a system’s energy per unit temperature is unavailable for doing useful (mechanical) work, often referred to as a systems degree of disorder.
What are the two equations that represent the thermodynamic definition of entropy?
dS = change in entropy
S = entropy
đQ = change in heat energy

What is the equation for entropy for 1 mole of an ideal gas?
đQ = change in heat energy
T = temperature
R = gas constant
V = volume

How can the equation for entropy be applied to an ideal gas?
1) Divide the first law of thermodynamics by T so that the LHS represents entropy.
2) Rewrite the equation, knowing that E = 3RT/2 and pV = RT.
3) Replace dT/T and dV/V with d(lnT) and d(lnV).
What is the equation for the Clausius inequality?
T = temperature of external heat reservoir
đQ = change in heat energy

Define the Clausius inequality
For an irreversible process, the heat entering the system at any point in the cycle must be less than or equal to zero.
What does the Clausius inequality say about the entropy of a system?
The change in entropy of a system must always be greater or equal to 0.
Define the law of increase in entropy
The entropy of an isolated system tends to a maximum.
What is the equation for the change in entropy when heat is passed from one object at a given temperature to another at a different temperature?

Write the first law of thermodynamics in terms of entropy

What are the Maxwell relations for the first law of thermodynamics?

What is the differential equation for isobaric specific heat capacity?

What is the differential equation for isovolumic specific heat capacity?

What is the equation for the change in entropy during a state change?
S = entropy
L = latent heat
T = temperature

What is the equation for the change in entropy during Joule expansion?

During Joule expansion, no work is supplied, and no heat is exchanged so the _______ ______ and the ________ is constant.
Internal energy
Temperature
Is Joule expansion reversible or irreversible?
Irreversible
How does the entropy of the system change in isothermal expansion compared to Joule expansion?
Isothermal: entropy increase
Joule: entropy increase
How does the entropy of the environment change in isothermal expansion compared to Joule expansion?
Isothermal: entropy decrease
Joule: no change
How does the total entropy change in isothermal expansion compared to Joule expansion?
Isothermal: no change
Joule: entropy increase
What is a thermodynamic potential?
Functions of state (quantities) with the dimension of energy that are used to represent the state of a system. They rely on Legendre transforms of the conjugate pairs p & V and S & T.
What are the 4 thermodynamic potentials?
- Energy
- Enthalpy
- Helmholtz free energy
- Gibbs free energy
When the change in energy has been _________, the system is stable.
Minimised
What are the natural variables in the equation for energy (E = E(_, _))?
- Entropy
- Volume
What is the equation to determine temperature using the differential equation for energy, E = E(S, V)?

What is the equation to determine pressure using the differential equation for energy, E = E(S, V)?

Define enthalpy
An energy-like thermodynamic potential that is the sum of the system’s internal energy and the product of its pressure and volume.
What is the equation for enthalpy in differential form?
H = enthalpy
T = temperature
dS = change in entropy
V = volume
dp = change in pressure

What are the natural variables in the differential equation for enthalpy (H = H(_, _))?
- Entropy
- Pressure
What is the equation to determine temperature using the differential equation for enthalpy, H = H(S, p)?

What is the equation to determine volume using the differential equation for enthalpy, H = H(S, p)?

What is the standard form of the equation for enthalpy?
H = enthalpy

Define Helmholtz free energy
An energy-like thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature and volume.
What is the equation for Helmholtz free energy in differential form?
F = Helmholtz free energy
S = entropy
dT = change in temperature
p = pressure
dV = change in volume

What are the natural variables in the differential equation for Helmholtz free energy (F = F(_, _)?
- Temperature
- Volume
What is the equation to determine entropy using the differential equation for Helmholtz free energy, F = F(T, V)?

What is the equation to determine pressure using the differential equation for Helmholtz free energy, F = F(T, V)?

What is the standard form of the equation for Helmholtz free energy?
F = Helmholtz free energy
E = energy
T = temperature
S = entropy

Define Gibbs free energy
An energy-like thermodynamic potential that defines how spontaneous a reaction is. It is equal to enthalpy minus the product of entropy and absolute temperature.
What is the equation for Gibbs free energy in differential form?
G = Gibbs free energy
S = entropy
dT = change in temperature
V = volume
dp = pressure

What are the natural variables in the differential equation for Gibbs free energy (G = G(_, _)?
- Temperature
- Volume
What is the equation to determine entropy using the differential equation for Gibbs free energy, G = G(T, p)?

What is the equation to determine volume using the differential equation for Gibbs free energy, G = G(T, p)?

What is the standard form of the equation for Gibbs free energy?
G = Gibbs free energy
E = energy
T = temperature
S = entropy
p = pressure
V = volume

What processes use the energy equation, E = E(S, V)?
- Isolated systems
- Mechanical equilibrium
What processes use the enthalpy equation, H = H(S, p)?
- Flow processes
What processes use the Helmholtz free energy equation, F = F(T, V)?
- Chemical reactions at fixed volume
What processes use the Gibbs free energy equation, G = G(T, p)?
- Phase equilibrium
What are the four differential equations for thermodynamic potentials?

What are the 4 differential equations that form the Maxwell relations?

What is the equation for the difference between isobaric and isovolumic heat capacity (not containing entropy)?

How can the entropy be eliminated from the equation for the difference in isobaric and isovolumic heat capacity?
1) Write change in entropy as a differential equation.
2) Divide this equation by dT at a fixed pressure.
3) Substitute the two heat capacity equations into this equation.
4) Eliminate the entropy term using the third Maxwell relation and rearrange.
Define isobaric expansivity
The fractional volume increase with temperature at a fixed pressure.
What is the equation for isobaric expansivity?
βₚ = isobaric expansivity
V = volume
T = temperature

Define isothermal compressibility
The fractional volume decrease with pressure at fixed temperature.
What is the equation for isothermal compressivity?
κₜ = isothermal compressibility
V = volume
p = pressure

What is the equation for the ratio of isobaric expansivity to isothermal compressibility?
p = pressure
T = temperature
βₚ = isobaric expansivity
κₜ = isothermal compressibility

What is the equation for the difference between isobaric and isovolumic heat capacity in terms of isobaric expansivity and isothermal compressibility?
C = heat capacity
V = volume
T = temperature
βₚ = isobaric expansivity
κₜ = isothermal compressibility

Define adiabatic compressibility
The adiabatic equivalent of isothermal compressibility. This is the fractional decrease in volume with pressure at a fixed value of entropy.
What is the equation for adiabatic compressibility?
κₛ = adiabatic compressibility
V = volume
p = pressure

What is the equation for the ratio between isothermal and adiabatic compressibility?
κₜ = isothermal compressibility
κₛ = adiabatic compressibility

How can the ratio between isobaric and isovolumic heat capacity be derived using the ratio between isothermal and adiabatic compressibility?
1) Apply the reciprocity theorem to both halves of the equation.
2) Apply the reciprocal theorem to both halves of the equation so that the ∂V terms are on the top of the fraction and the ∂p terms are on the bottom.
3) Cancel ∂V and ∂p terms using the chain rule.
4) Substitute the heat capacity terms into the equation.
What is the ratio between the isobaric and the isovolumic heat capacity equal to?
The adiabatic index
What is the Joule coefficient (give the differential that describes it)?
A coefficient that describes small temperature changes for the Joule expansion of a real gas.

What is the equation for the Joule coefficient in terms of isovolumic heat capacity, temperature, and pressure?
αⱼ = ∂T/∂V = Joule coefficient
Cᵥ = isovolumic heat capacity
T = temperature
p = pressure

The Joule coefficient is ____ ____ 0 for an ideal gas and ____ ____ 0 for a real gas, meaning that temperature increases as volume increases in a Joule expansion.
Equal to
Less than
What is a flow process?
A process in which a fluid flows steadily through a controlled volume. The properties of the fluid can change as it moves through the volume if work is done on it or heat is supplied.
________ is assumed to be conserved for a flow process if no work or heat is supplied by the process.
Enthalpy
What are the equations for initial and final enthalpy in a flow process?
H = enthalpy
E = energy
p = pressure
V = volume

What is the equation for the change in enthalpy in a flow process (using the first law)?
dH = change in enthalpy
Q = heat supplied by process
W = work done by process

What is the Joule-Kelvin expansion?
The restricted expansion of a gas within a container with two chambers. The gas flows from the first chamber, through a small opening or a porous plug, into the other chamber. In this process enthalpy is constant.

What is the differential used to define the Joule-Kelvin coefficient?
T = temperature
p = pressure

What is the equation for the Joule-Kelvin coefficient in terms of isobaric heat capacity, temperature, and volume?
αⱼₖ = ∂T/∂p = Joule-Kelvin coefficient
Cₚ = isobaric heat capacity
T= temperature
V = volume

The Joule-Kelvin coefficient is ______ ____ 0 for an ideal gas and for a real gas it is usually _______ at high pressures and ________ at low pressures.
Equal to
Negative
Positive
Define phase equilibrium
The state of a thermodynamic system, in which the different phases of the substance with a common boundary surface do not vary quantitatively.
What is the equation for the availability of a system?
A = availability
E = energy
T₀ = temperature of surroundings
S = entropy
p₀ = pressure of surroundings
V = volume

What is the differential form of the equation for availability?
dA = change in availability
dE = change in energy
T₀ = temperature of surroundings
dS = change in entropy
p₀ = pressure of surroundings
dV = change in volume

In a system where heat is flowing from the surrounding into the system the change in availability, dA, _ 0.
≤
The availability, A, is always ________ at equilibrium, so dA _ 0.
Minimised
When a system is thermally isolated (dS = 0) and has a fixed volume (dV = 0) what is the equation for availability?
dE = change in energy

When a system is thermally isolated (dS = 0) and has a pressure balance (p = p₀) what is the equation for availability?
dH = enthalpy

When a system is in thermal contact (T = T₀) and has a fixed volume (dV = 0) what is the equation for availability?
dF = Helmholtz free energy

When a system is in thermal contact (T = T₀) and has a fixed volume (p = p₀) what is the equation for availability?
dG = Gibbs free energy

When a system is thermally isolated and at a fixed volume, the _______ _______ is minimised for equilibrium state.
Internal energy
When a system is thermally isolated and pressure is balanced, the _______ is minimised for equilibrium state.
Enthalpy
When a system is in thermal contact and at a fixed volume, the _______ ____ ________ is minimised for equilibrium state.
Helmholtz free energy
When a system is in thermal contact and at a fixed volume, the ____ ____ _______ is minimised for equilibrium state.
Gibbs free energy
Define specific Gibbs free energy
The Gibbs free energy per unit mass, described by the symbol g.
What is the equation for the total Gibbs free energy?
G = Gibbs free energy
M = mass
g = specific Gibbs free energy

In phase equilibrium, the change in Gibbs free energy is _ so the specific Gibbs free energy is the same for all coexisting phases.
0
Along a phase boundary on a p-T plot, the specific Gibbs free energy is ___ _____ for the two coexisting planes. This means that small changes in the Gibbs free energy are also _____ ______.
The same
The same
What is the equation for the Clausius-Clapeyron relation?
dp = change in pressure
dT = change in temperature
l = specific latent heat
T = temperature
v = specific volume
L = latent heat
V = volume
Define the third law of thermodynamics
As a system approaches absolute zero, all processes cease and the entropy of the system approaches a minimum value (zero). This means that absolute temperature cannot be achieved for equilibrium phases.
What is cryogenics?
The Physics and engineering of low temperatures.
What is the equation for the entropy change between two temperatures at a fixed volume?
S = entropy
Cᵥ = isovolumic heat capacity
T = temperature

What happens to the heat capacity of a system at low temperatures?
It tends to zero.
What happens to the expansion coefficient as temperature tends to 0?
It also tends to zero, following the fourth Maxwell relation.
What is the equation for the first law of thermodynamics in terms of magnetisation energy?
dE = change in energy
T = temperature
dS = change in entropy
B = magnetic field
dM = change in magnetisation

How to pressure and volume relate to the magnetic field and magnetisation?
- Pressure is equivalent to minus the magnetic field.
- Change in volume is equivalent to the change in magnetisation.
What are the equations for magnetic field and magnetisation in thermodynamics?
B = magnetic field
µ₀ = permeability of free space
H = enthalpy
M = magnetisation
χ = susceptibility

Define Curie’s law
The susceptibility of a material is inversely proportional to absolute temperature.
What is the equation for Curie’s law?
χ = susceptibility
A = constant
T = temperature

What is the (approximated) equation for magnetisation when the magnetisation is much smaller than enthalpy?
M = magnetisation
χ = susceptibility
B = magnetic field
µ₀ = permeability of free space
A = constant
T = temperature

What is the equation for the adiabatic demagnetisation constant?
α = ∂T/∂B = adiabatic demagnetisation constant
B = magnetic field
µ₀ = permeability of free space
A = constant
T = temperature
C = heat capacity at a constant magnetic field

What is the equation for the equation for heat capacity as a function of an applied magnetic field?

Define probability
The extent to which an event is likely to occur, measured by the ratio of the favourable cases to the whole number of cases possible.
What is the equation for the number of possible ways to choose n from k distinct options?
nCk = number of ways to choose a given option
n = chosen options
k = number of distinct options

Describe lottery probability
An example of probability in which 6 numbers are chosen out of 49 with C(49, 6) ways of choosing 6 numbers. The probability of having a matching number is 6/49 and the probability of having a non-matching number is 43/49.
Describe poker probability
An example of probability in which there are 52 cards and 5 cards in a hand do C(52, 5) combinations of hands. Each different combination has a different combination that depends on the faces chosen (out of 13), and the suits chosen (out of 4).
Describe game show probability (probability of finding a prize hidden in a box)
In a game show where there is a prize in one of three boxes and the host removes one, the probability of finding the prize depends on whether or not the host knows where the prize is.
Describe disease testing probability
The probability of getting a true positive on a disease test depends on how accurate the test is and if there is any prior information given.
Define priori probability
The likelihood of an event occurring when there is a finite amount of outcomes and each is equally likely to occur, such as in a lottery of a poker game.
Define posteriori probability
The revised or updated probability of an event occurring after taking into consideration new information.
What is a macrostate?
A thermodynamic state of a system, defined by functions of state such as temperature, pressure, or volume.
What is a microstate?
A specific quantum state of a system that specifies all relevant information of all particles such as particle position, velocity, energy, or spin. Miscrostates encompass all individual particle variations.
Define the principle of equal a priori probability (PEAPP) also known as the principle of equal equilibrium probability
When an isolated system reaches equilibrium, all microstates accessible to it are equally probable.
What is the equation for statistical temperature at a fixed volume?
T = statistical temperature
k_B = Boltzmann’s constant
W = number of accessible microstates
E = energy

What is the equation for thermodynamic temperature at a fixed volume?
T = temperature
S = entropy
E = energy

What is the equation for statistical entropy?
S = entropy
k_B = Boltzmann’s constant
W = number of accessible microstates

Is thermodynamic temperature equal to statistical temperature?
Yes
What is the equation for the entropy of a system in a specific macrostate?
S = entropy
k_B = Boltzmann’s constant
i = i-th macrostate
Wᵢ = available microstates
Pᵢ = Wᵢ/W = probability to be in i-th macrostate
W = total number of microstates

What is the equation for the change in entropy caused by moving between microstates?
∆S = change in entropy
k_B = Boltzmann’s constant
P₁/P₂ = relative probability

What is the equation for the relative probability between initial and final states in a Joule expansion?
N = Avogadro’s number (= number of particles)

What is the equation for the overall change in entropy for the Joule expansion for 1 mole of gas?
∆S = change in entropy
k_B = Boltzmann’s constant
N = Avogadro’s number

Statistically, heat will only flow if there is an ________ in the total number of microstates when energy is being transferred from one place to another.
Increase
How can entropy be defined statistically?
Increase in entropy is the flow from a less probable state to a more probable state.
What is the equation for the statistical distribution of N particles between two equal-volumed, connected boxes? (The probability of being in one of the boxes)
P(N₁) = the probability of being in the first box
Wₜₒₜ = the total number of microstates (number of combinations) = 2ⁿ
W(N₁) = the number of ways of choosing N₁ from N

What is Stirling’s formula used for?
It is an approximation used to handle factorials in statistical calculations for large values of N.
What is the equation for Stirling’s formula?

What is one of the uses for Stirling’s formula?
To show the probability distribution at small deviations from equilibrium (it is a Gaussian distribution).
What is the variance and the mean for a large number, N, of independent random variables?
x = variable
x̄ = mean
N = number of variables
σ² = variance

What is the variance of the Gaussian distribution for the mean of a large number of independent, random variables? (Law of large numbers)

Is entropy extensive in equilibrium? Why?
Yes
Using Stirling’s formula, ∆S = 0 at equilibrium so entropy is extensive.
What value of entropy should be used for calculations of functions of state? Why?
The most probable entropy value should be used as entropy is extensive.
What is an ensemble?
A collection of identical systems, whose statistical fluctuations are cancelled out upon averaging.
What is a micro-canonical ensemble?
A system with a fixed total energy, E, and a fixed number of particles, N.
What is a canonical ensemble?
A system with a fixed number of particles, N, but in contact with a heat bath of fixed temperature, T.
What is a grand canonical ensemble?
A system free to exchange both particles and heat with the surroundings.
What is the Boltzmann distribution?
A probability distribution that describes the probability of finding a system in a particular microstate, used for canonical ensembles. The normalisation constant for this distribution is called the partition function.
What is the equation for the Boltzmann distribution?
pᵢ = probability of finding the system in a given microstate
Z = partition function
Eᵢ = energy of microstate

What is the equation for the partition function?
Z = partition function
Eᵢ = energy of microstate

What is the Gibbs entropy formula?
S = entropy
pᵢ = probability of finding the system in a given microstate

What is the Gibbs entropy formula used for?
It is used as an alternative to the Boltzmann distribution for canonical ensembles because it is easier to apply.
For a micro-canonical ensemble, the Gibbs entropy formula is _____ __ to the Boltzmann formula.
Equal to
Define Shannon’s theorem
If pᵢ is a set of mutually exclusive probabilities then f(p₁, p₂, p₃, …) = Σpᵢ lnpᵢ is the function which, when maximised, gives the most likely distribution of pᵢ, subject to any given set of constraints.
The maximum of f(pᵢ) represents the most likely and most random state so it is the state of maximum entropy.
Give four examples of systems that use the Boltzmann distribution
- Two-level systems
- Paramagnets
- Harmonic oscillators
- Random walk polymers
Define the partition function
A function of thermodynamic state variables that connects microscopic statistics to macroscopic thermodynamics.
The partition function is the _________ for the Boltzmann distribution.
Normalisation
What is the equation for the partition function?
Z = partition function

What is the equation for Gibbs entropy in terms of the partition function?
S = entropy
Z = partition function

Write the equation for Gibbs entropy in terms of the partition function (when the total energy is known)?
E = energy
T = temperature
S = entropy
Z = partition function

What is the equation for the Helmholtz free energy in terms of the partition function?
F = Helmholtz free energy
Z = partition function

What is the equation for pressure in terms of the partition function?
p = pressure

What is the equation for entropy in terms of the partition function?
S = entropy

What is the equation for isovolumic heat capacity in terms of the partition function?
C = heat capacity
T = temperature

What is the equation for energy in terms of the partition function?
E = energy
T = temperature
S = entropy
F = Helmholtz free energy

What is the 1D Schrödinger equation (time independent)?
φ(x) = wavefunction
V(x) = potential energy
E = energy

What is the general solution to the time dependent Schrödinger equation for a particle in a 1D box?
φₙ(x) = wavefunction
Eₙ = energy

What is the equation for the translational partition function?
Z = partition function
γ = α/k_B*T

What is the simplified equation for the translational partition function?

Define the thermal de Broglie wavelength
The de Broglie wavelength with a momentum that results from random thermal motion
What is the general solution to the time dependent Schrödinger equation for a particle in a 3D box?
φₙ(x) = wavefunction

What is the equation for the translational partition function in three dimensions?
Z = partition function

What is the simplified equation for the translational partition function in three dimensions?
Z = partition function

What is the equation for an independent, quadratic form of energy?
E = energy
α = energy term
q = constant

What is the equation for the equipartition theorem for one independent mode?
<E> = average energy
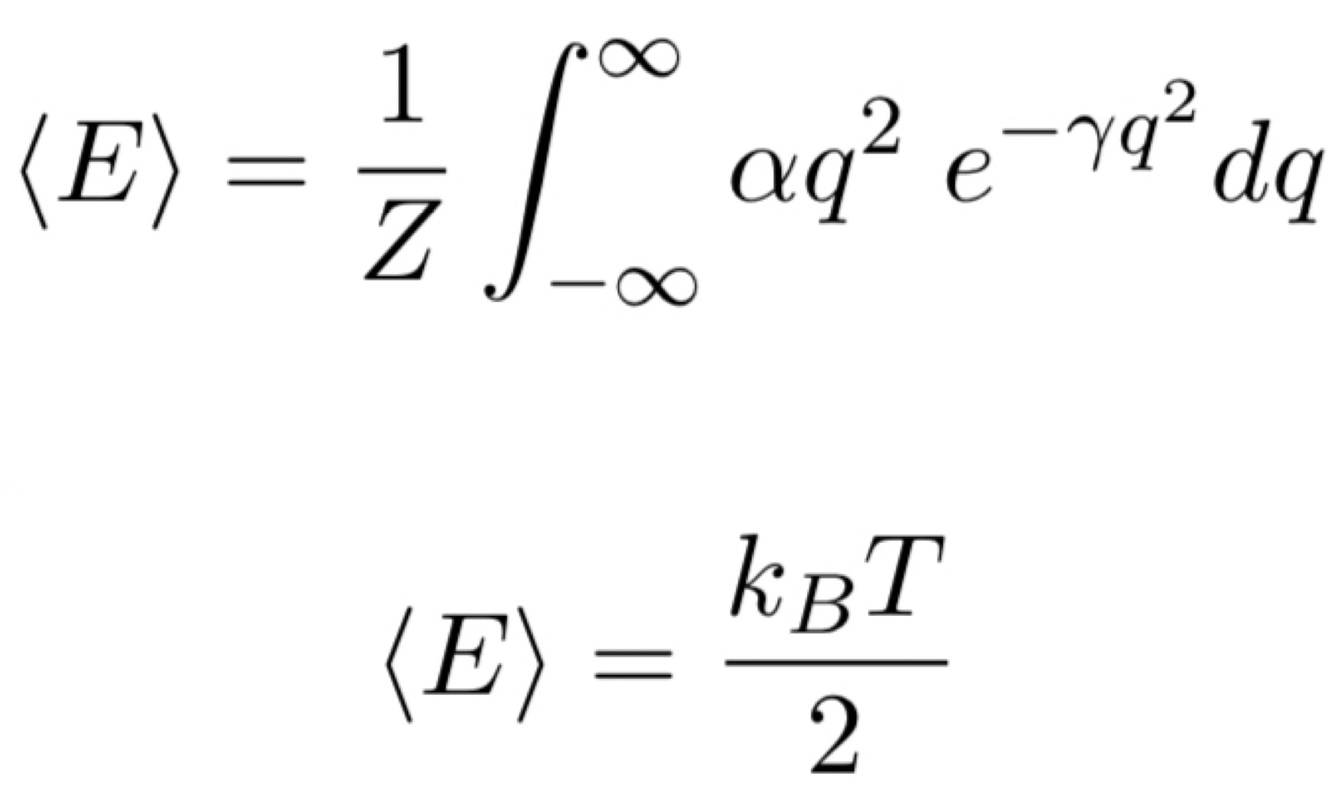
</E>
When does the equipartition theorem fail?
In quantum physics, because variables are generally quantised instead of being continuous.
What is the partition function for a diatomic molecule?
Z = partition function

What are the rotational energy modes of a particle?
E = rotational energy
l = angular quantum number
I (i) = interia

What is the partition function for rotational energy?
Z = partition function

What are the vibrational energy levels of a particle?
E = vibrational energy

What is the partition function for vibrational energy?
Z = partition function

The partition function for vibrational energy is the sum of a _______ series.
Geometric


