S2 Electricity COPY

Question 1

1. Describe what is meant by a complete circuit.

Answer 1

A complete circuit starts at one end of a power supply and continues to the other end with no gaps.

Question 2

2. Define series and parallel circuits.

Answer 2

Series circuits only have one route.

Parallel circuits have more than one branch.

Question 3

3. State the basic properties of series circuits:

What happens when more bulbs are added?

What happens when one bulb breaks?

Answer 3

As more bulbs are added, existing bulbs get dimmer.

(If the bulbs are identical they will have the same brightness as each other.)

If one bulb breaks, the rest go out.

Question 4

3. State the basic properties of parallel circuits:

What happens when more bulbs are added?

What happens when one bulb breaks?

Answer 4

As more bulbs are added, there is no change in the brightness of existing bulbs.

(If the bulbs are identical they will have the same brightness as each other.)

If one bulb breaks, the rest are unaffected.

Question 5

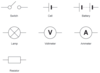
4. Draw the circuit symbols for a battery, cell, switch, lamp, voltmeter, ammeter and resistor.

Answer 5

Question 6

4. Identify the following circuit symbols.

Answer 6

Question 7

5. What are the rules for drawing neat circuit diagrams?

Answer 7

Neat circuit diagrams should be drawn with a pencil and a ruler, making sure the symbols are correct and that there are no gaps. The wires are drawn as straight lines with right angles. Symbols are not placed in corners. e.g.

Question 8

6. Define what a conductor is and give 2 examples.

Answer 8

A conductor is a material which allows electricity to flow

e.g. copper, iron

Question 9

6. Define what an insulator is and give 2 examples.

Answer 9

An insulator is a material which does not allow electricity to flow

e.g. rubber, glass.

Question 10

7. Describe what electrical current is.

Answer 10

Electrical current is a flow of charge.

Usually the charges are electrons, which flow away from the negative end of a battery and towards the positive.

Question 11

8. Draw circuit diagrams to show the correct positions of an ammeter and voltmeter in a circuit.

Answer 11

An ammeter (to measure current) is always added in series and a voltmeter (to measure voltage) in parallel. E.g.

Question 12

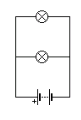
9. State the rule for current in series circuits.

Answer 12

In a series circuit the current is the same at all positions.

Question 13

10. State the rule for voltage in series circuits.

Answer 13

The sum of the voltages across components in series is equal to the supply voltage.

Question 14

9.&10. Example

A 5.5V battery is connected across 2 bulbs in series.

Bulb 1 has a voltage of 2V. What is the voltage across bulb 2?

The current through bulb 1 is 2A. What is the current through bulb 2?

Answer 14

V<sub>S</sub> = 5.5V (s for supply)
V<sub>1</sub> = 2V
V<sub>2</sub> = ?

V<sub>S</sub> = V<sub>1 </sub>+ V<sub>2</sub>
5.5 = 2 + V<sub>2</sub>
V<sub>2</sub> = 5.5 - 2 = 3.5V

I₂ = I₁ = 2A

Question 15

11. State the rule for current in parallel circuits.

Answer 15

The sum of the currents in parallel branches is equal to the supply current.

Question 16

12. State the rule for voltage in parallel circuits.

Answer 16

The voltage across components in parallel is the same as the supply voltage for every component.

Question 17

11.&12. Example

What will the voltmeter and ammeter in this circuit read?

Answer 17

The voltmeter will read 3V since the voltage across every component is the same as the supply voltage.

I<sub>S</sub> = 0.6A (s for supply)
I<sub>1</sub> = 0.1A
I<sub>2</sub> = ?
I<sub>3</sub> = 0.2A

I_S = I₁ + I₂ + I₃
0.6 = 0.1 + I₂ + 0.2 = 0.3 + I₂
I₂ = 0.6 – 0.3 = 0.3A
The ammeter will read 0.3A

Question 18

13. Explain the function of switches connected in series.

Answer 18

When more than one switch is connected in series they all have to be closed to complete the circuit and allow current to flow.

Question 19

13. Explain the function of switches connected in parallel.

Answer 19

When more than one switch is connected in parallel, any one (or more) can be closed to complete the circuit and allow current to flow.

Question 20

14. Describe what is meant by electrical resistance.

Answer 20

Electrical resistance is the ability of an object to reduce (or oppose) the flow of current.

Question 21

15. Describe the relationship between voltage and current
    and what a V-I graph looks like for a resistor.

Answer 21

Voltage and current are directly proportional for a resistor.

OR The voltage divided by the current will always give the same answer for a resistor.

A graph of V versus I will be a straight line through the origin:

Question 22

16. Define the numerical value of resistance.

Answer 22

Resistance is defined as R=V/I

Question 23

17. Define the symbols and their units in the equation

V = IR

Answer 23

V - Voltage (V)

I - Current (A)

R - Resistance (Ω Ohms)

Question 24

17. Example:

Calculate the voltage across a 6 Ω resistor when 2 A of current flow.

Answer 24

R = 6 Ω
I = 2 A
V = ?

V = IR
V = 2x6
V = 12 V

Question 25

17. Example:

Calculate the current flowing when a 200 V supply is connected across a 4 kΩ resistor.

Answer 25

R = 4 kΩ = 4,000 Ω
I = ?
V = 200 V

V = IR
200 = Ix4,000
Ix4,000 = 200
I = 200/4,000
V = 0.05 A

Question 26

17. Example:

Calculate the resistance if a 40 V supply produces 2 mA of current.

Answer 26

R = ?
I = 2 mA = 0.002 A
V = 40 V

V = IR
40 = 0.002xR
0.002xR = 40
R = 40/0.002
V = 20,000 Ω

Question 27

18. Example of calculations involving the relationship R_T = R₁ + R₂ + R₃ for resistors in series:
    The total resistance of a series circuit is 70 Ω, and the value of the 1st resistor is 10 Ω and the 3rd is 20 Ω. Calculate the value of the 2nd resistor in this circuit.

Answer 27

R<sub>T</sub> = 70 Ω
R<sub>1</sub> = 10 Ω
R<sub>2</sub> = ? 
R<sub>3</sub> = 20 Ω

R<sub>T</sub> = R<sub>1</sub> + R<sub>2</sub> + R<sub>3</sub>
70 = 10 + R<sub>2</sub> + 20
70 = 30 + R<sub>2</sub>
R<sub>2</sub> = 70 – 30 = 40 Ω

Question 28

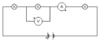
19. Example (see image)

a. Calculate the total resistance.
b. Calculate the current flowing in the circuit.
c. Calculate the voltage across the 12 Ω resistor.
d. Calculate the voltage across the 8 Ω resistor.

Answer 28

a. Use the rule for resistance in series
R_T = ? R_T = R₁ + R₂
R₁ = 12 Ω R_T = 12 + 8
R₂ = 8 Ω R_T = 20 Ω
b. Apply V=IR to the whole circuit
V = 30 V V = IR
R = 20 Ω 30 = I x 20
I = ? I x 20 = 30
I = 30/20 = 1.5 A
c. Apply V=IR to resistor 1
R = 12 Ω V = IR
I = 1.5 A V = 1.5 x 12
V = ? V = 18 V
d. Use the rule for voltage in series (NB there are other ways. You could apply V=IR to resistor 2)
V_T = 30 V V_T = V₁ + V₂
V₁ = 18 Ω 30 = 18 + V₂
V₂ = ? Ω V₂ = 30 – 18 = 12 V