Right Triangle Trigonometry

Question 1

What two concepts are useful for solving problems involving right triangles?

Answer 1

Pythagorean Theorem and SOH-CAH-TOA

Question 2

When you are given two sides of a right triangle, how do you find the third?

Answer 2

Pythagorean Theorem

Question 3

When using the Pythagorean Theorem, how do you decide which sides to plug in for a, b, and c?

Answer 3

c is the hypotenuse.
a and b are the legs

Question 4

What is the handy name that helps us remember the trigonometric functions for right triangles?

Answer 4

SOH - CAH - TOA

Question 5

Consider the triangle already labelled: HOW do we know which side is the hypotenuse?

Answer 5

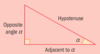
The hypotenuse is the longest side, and it is across the right angle.

Question 6

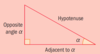
Consider this triangle. How do we know which side is the opposite?

Answer 6

Aside from the right angle, we need another angle inside the triangle (it is usually given to us) - here it’s “alpha”. The opposite side is opposite (right across from) angle alpha. This side will always depend on the angle you are focusing on. ALWAYS LABEL YOUR SIDES!

Question 7

How do we know which side is the adjacent?

Answer 7

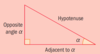
Adjacent means “next to”. So the adjacent side next to the angle - here it’s angle alpha again! This side will always depend on the angle you are focusing on ALWAYS LABEL YOUR SIDES.

Question 8

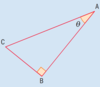
On the brand new triangle below, find the hypotenuse, the opposite and the adjacent sides:

Answer 8

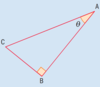
• Hypotenuse = side CA

(longest side, opposite the right angle)

• Opposite = side CB (opposite angle “theta”)
• Adjacent = side AB (“next to” angle theta)

Question 9

What does SOH - CAH - TOA stand for?

Answer 9

SOH - CAH - TOA

Question 10

What’s the general process for finding an unknown side of a right triangle using SOHCAHTOA (trigonometry)?

Answer 10

1. Label ALL your sides! H = hypotenuse, O = opposite, A = adjacent.
2. See which of the SOHCAHTOA functions fits the information you have (you can only have ONE unknown)
3. Write down the equation that you need and plug-in the information that you have.
4. Rearrange it so that your unknown is the subject of the equation (meaning, it’s left alone on one side of the equation).
5. Type in the other side of the equation into your calculator and solve.
6. Unless told otherwise, always express your answer to 3 significant figures (don’t forget to check if you need to round up!)

CAREFUL! Make sure your calculator is in degrees!

Question 11

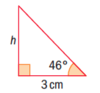
Consider the following triangle. Which function would you use to find side h?

Answer 11

• What sides do you have?

h (opposite), 3 (adjacent), and the angle is 46º

• What function fits opposite and adjacent?

TOA. tan(angle) = opposite/adjacent

tan(46º) = h/3

tan(46º)x3 = h

(now put the left hand side of this equation in you calculator - make sure it’s in degrees!)

Question 12

How do you find side x?

Answer 12

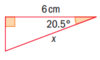
• What sides do you have?

x (hypotenuse), 6 (adjacent), angle 20.5º

• What function fits hypotenuse and adjacent?

CAH - cos(angle) = adj/hyp

cos(20.5) = 6/x

• Since x is in the bottom part of the fraction, multiply both side by x so you can cancel it on the left side of the equation:

cos(20.5) (x) = 6

Now divide both sides by cos (20.5)

x = 6/cos(20.5) = 6.41 (3 s. f.)

Question 13

What do we ALWAYS need to do to trig functions in order to find an unknown angle?

Answer 13

To find an unknown angle, we ALWAYS need to take the inverses of the trig functions.

Question 14

Find angle theta:

Answer 14

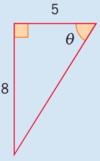
• What sides do we have? Opposite & adjacent
• What function fits opp & ajd?

TOA: tan(“theta”) = opp/adj = 8/5

therefore, “theta” equals the inverse tangent of 8/5 (as seen below)

Question 15

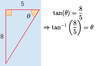
Find angle theta:

Answer 15

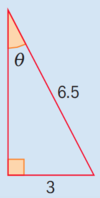
• What sides do we have? 3 (opposite) & 6.5 (hypotenuse)
• What function fits opp & hyp?

SOH: sin(theta) = opp/hyp = 3/6.5

therefore theta is equal to the inverse sine of 3/6.5 (as seen below)

Question 16

What is an “angle of elevation”?

Answer 16

It’s the angle between the floor and an upward line.

Question 17

What is an “angle of depression”?

Answer 17

It’s the angle between the ceiling and a downward line.

Question 18

What are angles of elevation and depression?

Answer 18

Question 19

What is the sine formula?

Answer 19

Question 20

What is the cosine formula?

Answer 20

Question 21

What is the tangent formula?

Answer 21

Question 22

What type of triangle do you need to have in order to use SOH CAH TOA?

Answer 22

A right angled triangle.

Question 23

What is the handy name that helps us remember the trigonometric functions for right triangles?

Answer 23

SOH - CAH - TOA

Question 24

How do you liberate an angle from a trig function?

Answer 24

Use the inverse!

Question 25

Any time you are working with trig ratios (sin, cos, tan), what calculator mode do you NEED to set?

Answer 25

DEGREES MODE!

(Press mode, then select degrees)

Question 26

When you have a right triangle, how do you know when to use Pythagorean Theorem vs. SOH CAH TOA?

Answer 26

Pythagorean Theorem is when you are given two sides and you are finding the third side.

If the problem involves an angle (either you are given an angle or trying to find an angle), use SOH CAH TOA.

Question 27

How would you use inverse trig to find this angle?

Answer 27

Question 28

When do you use Pythagorean Theorem?

Answer 28

when you are given two sides of a right triangle and you are trying to find the third

Question 29

How can you “show” that a triangle is a right triangle?

Answer 29

Show that the triangle satisfies the Pythagorean Theorem