Resistivity

Question 1

1. For the given Figure, give the equation for resistance.
2. Give the equation relating resistivity to conductuvity and the equation for conductivity.
3. Give the equation relating resistivity and sheet resistance for a uniformly doped region and non-uniformly doped region.

Answer 1

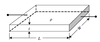
1. R = ρ(l/A) = ρ(l/Wt)

l = length, W = width, t = thickness

2. ρ = 1/σ

σ = q(nµ_n+pµ_p)

3. Uniformly doped: R_sheet = ρ/t

Non-uniformly doped: (see Figure)

Question 2

1. What is the advantage of the 2PP method of measuring resistivity over the 4PP method?
2. For the 4PP setup shown in Fig. 1.4(b), explain how ρ is measured and derive the relevant equations with given assumptions.

Answer 2

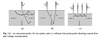
1. The total resistance of a 2PP measurement is given by the following:

R_T = 2R_c + 2R_sp + R_DUT + 2R_W

R_c = contact resistance, R_sp = spreading resistance, R_W = wire resistance

In a 4PP measurement, R_c and R_sp can be virtually eliminated by measuring sourcing current and measuring voltage with separate probes (i.e. using a high Z voltmeter). R_W can be eliminated using a sound experimental setup. R_T can be simplified to ≈R_DUT.

2. See the attached image for a derviation of ρ = 2πs(V/I).

s = probe spacing, I = current

This equation assums the sample is semi-infinite in extent in both the lateral and vertical directions. In reality a correction factor must be used:

ρ = 2πs(V/I)F.

Question 3

1. For the equation:

ρ = 2πs(V/I)F,

describe what impacts F and how it is determined.

2. If the sample thickness (t) is less than the probe spacing (s) and the probes are co-linear, indepedent correction factors can be used as follows:

F = F₁F₂F₃.

Otherwise this equation becomes more complicated. Give a description of each correction factor.

Answer 3

1. F is a correction factor that accounts for probe location near sample edges, finite sample thickness, finite sample diameter, probe placement and sample temperature.
2. F₁: depdendent on thickness and whether the underlying substrate is insulating (simpler) or conducting (more difficult experimentally)

F₂: dependent on lateral dimensions and is ≈1 when wafer diameter (D) is > 40s.

F₃: dependent on placement and is ≈1 when the probes are > 4s from sample edge (also probe should be centered in the doped region)

Question 4

1. When is the van der Pauw method primarily used?
2. Give the equation for ρ using van der Pauw method.
3. What are the five requirements for implementing the van der Pauw method.

Answer 4

1. Irregularly shaped samples.
2. See the attached image.

3.

1. Four contacts are made at the periphery
2. Contacts must be small
3. Contacts must be ohmic
4. Sample should have uniform thickness
5. Surface should be connected (i.e. no isolated holes, voids, etc.).