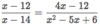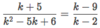Brainscape's Knowledge GenomeTM


Top Flashcards (Certified)
All Flashcards

Algebra 2 > Rational Expressions, Equations, and Functions > Flashcards

Rational Expressions, Equations, and Functions Flashcards

(64 cards)

Start Studying
1
Q

What is a ratio?

A

a fraction

numerator ÷ denominator

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What is a rational expression?

A

a ratio of polynomials

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

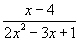
What is an expression?

A

a combination of numbers, variables, and operations

examples:

5 + 23

4x

6x + y²

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

How do you multiply rational expressions?

A
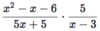
  1. factor numerators and denominators (find excluded values)
  2. cancel
  3. multiply
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

How do you simplify rational expressions?

A
  1. combine like terms
  2. factor numerators and denominators
  3. cancel
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What are excluded values?

A

values of x that make the denominator = 0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

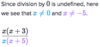
What is a complex fraction?

A

a fraction that contains a fraction in the numerator and/or denominator (a.k.a. nested fraction)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

How do you simplify complex fractions?

A
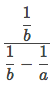
  1. add or subtract fractions if necessary
  2. rewrite as division: numerator ÷ denominator
  3. rewrite as multiplication: first fraction times reciprocal of second fraction
  4. factor numerators and denominators
  5. cancel
  6. multiply
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

How do you divide rational expressions?

A
  1. rewrite as multiplication: first fraction times reciprocal of second fraction
  2. factor numerators and denominators (note excluded values)
  3. cancel
  4. multiply
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

How do you add or subtract rational expressions?

A
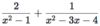
  1. factor denominators
  2. get common denominator by multiplying the numerator and denominator by any missing factors
  3. add or subtract the numerators; leave the denominator factored
  4. simplify
    1. combine like terms
    2. factor
    3. cancel
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

What are factors?

A

the polynomials being multiplied

factor × factor = product

example:

(x – 2)(x + 2) = x2 – 4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

What is a product?

A

the result of multiplying two or more polynomials

factor × factor = product

example:

(x – 2)(x + 2) = x2 – 4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

When subtracting, make sure to…

A

…distribute the negative.

example:

5 - (x + 6) = 5 - x - 6

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Dividing is the same as…

A

…multiplying by the reciprocal.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

You can cancel only if…

A

…numerators and denominators are factored.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

When adding or subtracting fractions, you need a…

A

…common denominator.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

What is a quotient?

A

the result of dividing two or more quantities

dividend ÷ divisor = quotient

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

How do you factor a trinomial?

A

GCF(trinomial)

–and/or–

(binomial)(binomial)
“multiplies to c and adds to b”

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

How do you factor a binomial?

A

GCF(binomial)

–and/or–

Difference of Squares

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

How do you multiply a binomial times a binomial?

A

distributive property

(a + b)(c + d)

a(c + d) + b(c + d)

ac + ad + bc + bd

example:

(x + 5)(x - 3)

x(x -3) + 5(x - 3)

x2 - 3x +5x - 15

x2 + 2x - 15

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

How do you multiply a monomial times a binomial?

A

distributive property

a(b + c)

ab + ac

example:

2bd(3bc + 5ad)

6b2cd + 10abd2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

What is a constant?

A

a number

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

What is a binomial?

A

a polynomial with two terms

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

What is a trinomial?

A

a polynomial with three terms

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
What is a **polynomial**?
an expression of **one or more terms**
26
What is a **term** (in an expression)?
a number, a variable, or numbers and variables **joined by multiplication or division** terms are **separated by addition or subtraction** in an expression
27
What is a **proportion**?
an equation with a **fraction** on **both sides**
28
How do you **solve** a **proportion**?
1. **factor** denominators 2. find **excluded values** 3. **multiply** just the numerator on both sides by factors to **cancel** factors in denominators; remember to distribute 4. get everything on **one side** (0 on the other side) and solve by **factoring** or **quadratic formula** 5. check for **extraneous solutions** (zeros *and* excluded values)
29
What is an **extraneous solution** of a function?
a **zero** (numerator = 0) that is **also an excluded value** (denominator = 0)
30
In an equation, if the variable is on **both sides**...
...get the variable on **one side**.
31
What is an **equation**?
two expressions that are **equal** to each other left expression **=** right expression
32
What is a **hole** (a.k.a. removable discontinuity)?
a **break** in the graph found at **canceled excluded values**
33
What is an **asymptote**?
a **line** that a graph **approaches** but **never intersects**
34
What is a **horizontal asymptote**?
an invisible horizontal line (y = constant) that a graph approaches but never intersects as x approaches -∞ or ∞
35
What is the **equation of a horizontal line**?
**y** = constant
36
What is the **equation of a vertical line**?
**x** = constant
37
What is a **vertical asymptote**?
an invisible vertical line (x = constant) that a graph approaches but never intersects as x approaches a **remaining excluded value**
38
How do you **graph** a rational function?
1. **factor** numerator and denominator 2. find **excluded values** (denominator = 0) 3. **cancel** 4. find **hole** (canceled excluded value) 5. find **vertical asymptote** (remaining excluded value) and graph 6. identify **domain** (all real #'s except excluded values) 7. find **horizontal asymptote** (none, y = 0, or y = ratio) and graph 8. identify **range** (all real #'s except horizontal asymptote) 9. **sketch** graph from calculator (don't forget holes!)
39
How do you find a **vertical asymptote**?
1. **factor** numerators and denominators 2. find **excluded values** (denominator = 0) 3. **cancel** 4. **canceled excluded values** are holes 5. **remaining excluded values** are vertical asymptotes
40
How do you find a **horizontal asymptote**?
Compare the degree of the numerator with the degree of the denominator: **top heavy**: no horizontal asymptote **bottom heavy**: y = 0 (plus or minus any vertical shifts) **equal degree**: y = ratio of coefficients
41
What is the **domain** of a rational function?
all real numbers **except excluded values** (denominator = 0: holes AND vertical asymptote)
42
What is the **range** of a rational function?
all real numbers **except the horizontal asymptote**
43
How do you find a **hole** (a.k.a. removable discontinuity)?
1. **factor** numerators and denominators 2. find **excluded values** (denominator = 0) 3. **cancel** 4. **canceled excluded values** are holes
44
What operation does a **fraction bar** represent?
**division**
45
What is a **difference**?
the **result of subtracting** two polynomials
46
What is a **quotient**?
the **result of dividing** two polynomials
47
How do you factor a **difference of squares**?
(**sum** of square roots)(**difference** of square roots)
48
What is a **monomial**?
a polynomial with **one term**
49
What is the **domain** of a function?
the set of all possible **values of x**
50
What is the **range** of a function?
the set of all possible **values of y**
51
What is a **variable**?
**a letter** representing a quantity that takes on different values
52
Which is the **independent variable**?
**x**
53
Which is the **dependent variable**?
**y** or **f(x)**
54
What can you do **after factoring** all numerators and denominators?
**cancel** common factors
55
What's the best way to **solve** this equation?
1. find **excluded values**: x ≠ -4 or 9 2. **add** the right side to get one fraction 3. **multiply** both sides by factors in denominators to **cancel** them; remember to distribute 4. get **everything on one side** (0 on the other side) and solve by **factoring** or **quadratic formula** 5. check for **extraneous solutions** (zeros *and* excluded values)
56
What does it mean to **solve** an equation?
**get the variable by itself** to find its value
57
What's the **first step** to **solve** this equation?
1. **factor** numerators and denominators 2. **cancel** **===** then, **multiply** both sides by fewest factors necessary to **cancel** denominators
58
If both fractions of a **proportion** have the **same denominator**, what can you do?
**multiply** both sides by that denominator to **cancel** them
59
What's the best way to solve this equation?
1. **factor** denominators 2. find **excluded values**: k ≠ 2 or 3 3. **multiply** just the numerator on both sides by factors to **cancel** factors in denominators: (k - 3) and (k - 2) 4. get everything on **one side** (0 on the other side) and solve by **factoring** or **quadratic formula** 5. check for **extraneous solutions** (zeros *and* excluded values)
60
When **multiplying** fractions, you multiply...
...numerators with numerators and denominators with denominators (straight across).
61
When **factoring**, first look for a...
...**GCF**. example: 3x2 + 6x - 45 \>\> *3 is the GCF* 3(x2 + 2x - 15) \>\> *factor by distributive property* 3(x - 5)(x + 3) \>\> *keep factoring if possible*
62
What is a **zero** (a.k.a. solution) of a function?
an **x-intercept** of the graph where **f(x) = 0**, which is when the **numerator = 0**
63
In a function, what do **excluded values** tell you?
**canceled**: hole (a.k.a. removable discontinuity) **remaining**: vertical asymptote
64
What does **f(x)** mean?
it's another way of writing the **y** variable (the dependent variable)

Algebra 2 (3 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions