R.40 Valuation of Contingent Claims

Question 1

put-call parity

Answer 1

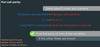
Protective put = Fiduciary call

Long stock + Long put = Long risk-free bond + Long call

S + p = PV(X) + c

Question 2

BSM model for stocks with dividend and without for:

• Call
• Put

Answer 2

Question 3

Delta sensitivities

Changes in option values

Answer 3

Delta values:

Long an underlying asset delta

= 1.0

b/c asset’s price is the value of the position.

Conversely, a short position of underlying asset delta

= -1.0

Delta of long at-the-money (ATM) call option

≈ 0.5

meaning that the value of this position will decrease by 0.5% for a 1% increase in the value of the underlying

Delta of short ATM call option

≈ -.5

Question 4

dynamic hedging

Answer 4

Question 5

One-period binomial model for European stock options

Hedge ratio

No-arbitrage approach to value calls, puts

Expectations approach to value calls, puts

Answer 5

Question 6

BSM - Key Interpretations

1. Calls
2. Puts
3. Risk neutral probabilities
4. Dividend paying stock options
5. Currency options

Answer 6

Key Interpretations of Black-Scholes Merton Model

Described as having two components: a stock component and a bond component:

1. Calls

• viewed as a leveraged investment in N(d₁ ) worth of _stock_ for every e^-rTN(d₂ ) worth of borrowed funds.
• c = SN(d₁) – e^–rTXN(d₂)

2. Puts

• viewed as long N( -d₂ ) worth of bond for every short position N ( -d ₁ ) value of stock.
• p = e^–rTXN(–d₂ ) – SN(–d₁ )

3. • N (d₂)* is risk-neutral probability of a call option expiring in- the-money.

N( -d₂ ) is the risk-neutral probability that a put option will expire in - the-money.

• 4. Dividend paying stocks*
• carry benefit (dividend yield) on underlying stock offsets cost of carry (risk-free rare) and reduces (increases) the value of call (put) option on the stock.
  5. Currency options
• Interest rate earned on foreign currency is the carry benefit.

Question 7

BSM Assumptions

Answer 7

Assumptions underlying rhe Black-Scholes-Merton (BSM) model are:

• Underling asset’s
  
  • return follows a lognormal distribution (b/c of geometric Brownian motion) meaning logarithmic (continuously compounded) return is normaly distributed.
  • price change is smooth and continuous
  • volatility and yield are constant and known
  • short-selling allowed w/ full use of proceeds
• (Continuous) Risk-free rate is constant and known
• Continuous trading at every instant.
• Markets are frictionless.
• European options used (cannot exercise early)
• No arbitrage opportunities exist in marketplace

Question 8

BSM inputs (the Greeks)

Answer 8

Question 9

Delta and Delta Hedging

Answer 9

Question 10

Gamma

Implied Volatility

Answer 10