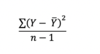R4 - Quant - Introduction To Linear Regression

Question 1

The 6 Assumptions of the Linear Regression Model

Answer 1

1) The relationship between the dependent variable Y, and the independent variable X is linear in the parameters b0 and b1. This requirement means that b0 and b1 are raised to their first power only and that neither b0 nor b1 is multiplied or divided by another regression parameter (as in b0/b1) The requirement does not exclude X from being raised to a power other than 1
2) The independent variable X is not random
3) The expected value of the error term is 0
4) The variance of the error term is the same for all observations.
5) The error term E is uncorrelated across observations. Consequently E(ei ej) = 0 for all i that are not equal to j)

►6) The error term, E, is normally distributed.

Question 2

SEE

(Standard Error of Estimate)

Answer 2

This is the standard deviation of the distribution of the Error Term

The smaller the SEE the more acurate the regression

B₀ & b₁ are estimated so we lose 2 degrees of freedom hence having n -2

Question 3

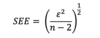
Error Term

Answer 3

The portion of the dependent variable that is not explained by the independent variable(s) in the regression.

Question 4

R²

^{Coefficient of Determination}

^{(Single Independent Variable)}

Answer 4

Measures the fraction of the total variation in the DV that is explained by the IV

if Only 1 IV square the correlation between DV & IV

r = P_XY =

Thus if r = .9203 then r² = 0.8470

Thus the IV explains 84.7% of the variation in Y

Question 5

R2

Coefficient of Determination

(Multiple Independent Variable)

Answer 5

Measures the fraction of the total variation in the DV that is explained by the IV

R² = 1 -

Question 6

Confidence Invterval for a regression coefficient

Answer 6

An interval of values that is believed to include the true parameter value of b₁ with a given degree of confidence.

Smaller Standard Deviation = tighter confidence Interval

Question 7

Hypothesis Testing

Answer 7

Level 2 only does T statistics

=

T = Test statisitic (Typically tested at µ = 5%

At this level the critical value is 1.96

Therefore anything with a T- Statistic of less than 1.96 can be rejected.

Question 8

Dependent Variable

Answer 8

The variable whose variation around the mean is to be explained by the regression.

The left hand side variable in a regression equation.

Usually called Y

y=f(x)

Question 9

Independent Variable

Answer 9

A variable used to explain the dependent variable in a regression;

a right-hand-side variable in a regression equation.

Usually called X

y=f(x)

Question 10

P Value

Answer 10

The smallest level of significance at which the null value can be rejected

Question 11

SSE

Answer 11

Sum of Squared Errors or residuals

Also known as residual sum of Squares

(The Unexplained)

Question 12

RSS

Answer 12

Regression Sum of Squares

This value is the amount of total variation in Y that is explained in the regression equation.

(The Explained)

Question 13

TSS

Answer 13

Total Sum of the Squares

TSS = SSE + RSS

TSS = The Unxplained + The Explained
(SSE) (RSS)

Question 14

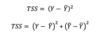
ANOVA

Answer 14

ANalysis Of VAriance

Determine the usefulness of the IVs in explaining the variance in the DV

ANOVA provides the inputs for an F-Test of the sig

Question 15

Estimated parameters

Answer 15

With reference to a regression analysis, the estimated values of the population intercept and population slope coefficient(s) in a regression.

Question 16

Fitted parameters

Answer 16

With reference to a regression analysis, the estimated values of the population intercept and population slope coefficient(s) in a regression.

Question 17

Linear regression

Answer 17

Regression that models the straight-line relationship between the dependent and independent variable(s).

Question 18

Regression coefficients

Answer 18

The intercept and slope coefficient(s) of a regression.

Question 19

ANOVA F Statistic

Answer 19

Question 20

(3) Limitations of Linear Regression

Answer 20

1. Regression relations can change over time
   e.g. Parameter instability
   Sensitive to:
   - Time Period Selected
   - Sampling from more than 1 population
2. What works only works if it is kept secret
   - Public knowledge may negate usefulness
3. Output dependent on regression assumptions
   - tests can be performed on the €
   - typically not unequivocal

Question 21

Parameter instability

Answer 21

The problem or issue of population regression parameters that have changed over time.

Question 22

Sample Variance
of the Dependent Variable

Answer 22

or