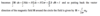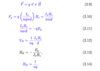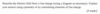Questions & General Notes Flashcards
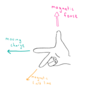
Sketch the electric field around an electric dipole.
Include equipotential lines and the direction of the field.
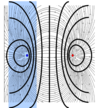
Sketch the Electric Flux Density around a sharp conducting rod, raised to a potential V.
Explain why this is suitable for a lightning conductor.
Taking part of the conductor as a sphere with radius a then the field at the surface of the conductor is…
Solve using boundary conditions.
Important to remember the how the components relate for two different dielectrics.
How would you solve this problem?
First, calculate the LHS of Gauss’s law, which looks at the surface area. If the surface is spherically symmetrical, the flux is leaving radially and the magnitude is uniform, so D can be considered a constant and factored out of the integral. The resulting integral simply calculates the total surface area.
Next, you look at the RHS of the equation and calculate the integral of the charge density over the volume v. Since the charge density is constant it can be factored out of the equation.
The two results are equated to eachother to find D.
The final expression needs to include the vector direction. This is done by multiplying D by the unit vector of r. You also need to remember to include the radial direction, which in this case is negative.
To find the electric flux density outside of r, the calculations need to adjusted. RHS of the equation stays the same, but for the LHS r becomes a, since the spherical cloud is limited by radius a, it doesn’t go any further…
If you need to apply Gauss’s law to a sphere and there is spherical symmetry, what can you assume about the equation describing the total flux leaving the Gaussian surface?
Since the sphere is symmetrical all around, the flux leaves the surface radially. As a result, the dot product of D and dS is essentially equal to the product of the magnitude of the two. With the magnitude being uniform, D can be taken out of the integral as a constant for the fixed radius (if the magnitude of D changed this wouldn’t be possible).
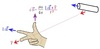
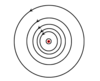
The figure shows the current carrying wire and an element dl somewhere along the wire at a distance r from the point at which the magnetic flux density B is required. The Biot Savart law gives the direction (out of the page in this case) from the cross product in the equation. It also gives the magnitude of dB due to just that small element of current I.
Magnetic Field around a straight current carrying wire, coming out of the page.
What do the dot product and cross product represent?
The dot product of two vectors A and B is the length of the projection of A onto B multiplied by the length of B.
The magnitude of the cross product is the area of a parallelogram (four-sided rectangular figure) with two sides based on vectors A and B. The direction of the cross product is orthogonal to the plane containing this parallelogram.
In other words, the cross product is a geometric construction that gives a vector perpendicular to two other vectors and the resultant vector has a length equal to the area of the parallelogram.
What do you do in this case?
You have to equate the x component to zero.
Using Gauss’s law, what is the flux through a spherical shell of radius R with
When you’re determining the electric field outside of a shell of uniformly distributed charge, what can you immediately assume?
That the charge enclosed is equal to the charge coming from the shell.
Thus when taking the Gaussian surface greater than the radius of charged shell, the shell can be essentially considered a point charge.
How do you solve this?
In the first line they determined that the integral of D.ds could be written as 4πr2 .
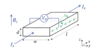
What is the total flux leaving the cube?
Anything you need to remember?
That in a uniform field, objects will not have a net flux leaving it.
What should you not forget when using electric field equations or calculating them using gauss’s?
the unit vector:
ar
What is the potential difference?
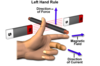
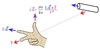
Right hand rule for biot-savart.
middle finger is the unit vector
index is Idl
thumb is the direction of dB
When asked to draw a vector field, what do you need to remember?
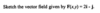
That’s it’s a field, and thus implies multiple vectors…
What do you need to remember about this question?
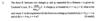
Although marks were awarded for if only x and y were included, z should be written down as well.
What is a expression for force that you need to remember for the exam?
As it isn’t given in the formulaa sheet.
For a length of wire l this becomes: F = I*L*uLx B
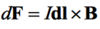
What did you learn about this question?
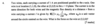
If no electric field is defined, and they only talk about electric fields, do not use the full lorentz force eq.
Also, that you can use: dF = IdLxB
RH rule for magnetic field, current and force.
What shape do lines of vector B make around a line of current? …
AC signals through capacitors and inductors
The capacitor is continuously charging and then discharging as the alternating voltage appears across the capacitor plates. When the capacitor is fully charged there is an electric field between the capacitor plates. The energy is stored in the electric field. In the case of the inductor, the current flowing through the wire generates a magnetic field; the energy is stored in the magnetic field.
How can you derive relative permittivity?
P = ε0XE
Sketch diagram of the electric field going through both dielectrics.
What did you learn from this?
In first capacitor, the normal component is continuous and so E will vary in each dielectric.
For the second capacitor, the tangential component is continuous so the same field is in both dieletric regions…
remember this, when its tangential, its the same field.
Explain the operation of a lightning conductor
By using gauss’ law…
What does this flux symbol represent?
The flux in circuit 2 due to circuit 1.
Outline how the inductance between two loops is obtained.
Go through the whole process.
Calculate the total magnetic flux density at the center of a loop of radius r and length l.
Derive magnetic field H, at a distance r around a long straight wire carrying current I.
The steps are as follows:
The dot product, H.dc can be converted to Hdc because they are parallel. Since the size of H is the same around the circle, H can be factored out of the integral.
Lastly, the total dc is the circumference.
How do you determine the direction of a magnetic field at the centre of the loop ?
middle finger is unit vector direction, index is direction, of current with dl
Then the direction of the thumb gives you the direction of the magnetic field.
Sketch the Hall effect.
Include all details in the diagram.
I must be perpendicular to B
The voltage produced must be perpendicular to both of them.
Derive RH = 1/nq
Hall coefficient is defined as RH = Ey/(JxBz)
Knowing that Jx = Ix / wd
RH can be plugged into equation 2.11 and rearranged for to obtain 1/nq
Calculate ii) the doping concentration of the doped silicon.
When calculating the doping concentration from the hall effect, what do you need to remember?
That d is the thickness of the block or sheet of the doped silicon.
That the units of concentration are m-3
State and explain how you would expect the Hall voltage to change as the temperature of the sample is lowered.
Hall voltage should increase. Lower temperature means fewer carriers, hence larger RH and VH.
What is the equation for the magnetic force on a current carrying wire due to a magnetic field?
How can you derive it from the formula booklet?
Start with Lorentz Force.
Theta is between current and magnetic flux density.
Calculate net force on rectangular loop.
Sketch the magnetic flux density around a loop of wire carrying a current I. Show the magnetic flux density close to the wire and at a distance in your diagram(s).
What so you need to remember when they say “diagram(s)”?
Diagram(s) most likely implies that you need draw more than 1 diagram…
And in this case its true… especially since they highlight two instances they want to be sketched.
What does this integral represent and what are the two things it’s equal to?
Em is the electric field produced by the changing magnetic flux.
Taking the closed loop integral of the electric field produced by the changing magnetic flux gives you the induced voltage Vemf.
It is also equal to the surface integral of the magnetic flux density.
What do you have to remember about these types of questions?
That a Gaussian surface inside an object with surface charge density leads to a result of zero for the electric flux density or electric flux.
“A cylinder is a suitable shape because the symmetry of the charge distribution is cylindrical. It allows for the canceling of surfaces that flux passes through, the flat areas of the cylinder, as they are equal and opposite magnitude. This then only leaves the components radial to the axis of the cylinder. Inside the cylinder, a Gaussian surface is constructed, but there is no charge inside the Gaussian surface, so the Electric flux density is zero inside the cylinder.”
?
The capacitance between c and e ?
The plate can be treated as two equal parallel capacitors.
Plot the magnitude of the Electric Field and Electric Flux Density as a function of R through a coaxial cable…
When you see a loop in a magnetic field, what should you straight away think of?
Faraday’s law.
What is the solution?
What is the direction of the current knowing that the magnetic field is into the page?
How can you determine the direction of a force on charged particles in a magnetic field if you know the direction of the current and direction of the magnetic field?
Flemings left hand rule.
Explain this equation
It says that the total induced electric field (electric field created by the changing magnetic flux around a closed loop is equal to the (-)ve change in magnetic flux density across the surface of the surface of the loop.
So a changing magnetic flux across a surface produces an electric field around a closed loop that opposes the change.
The magnetic flux at the center of the circular loop…
Describe the Electric field from a line charge (using a diagram as necessary). Explain your answer using symmetry or by considering elements of line charge
