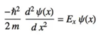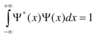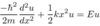Quantum mechanics Flashcards
Give the Schrödinger equation in its most basic form
H is the Hamiltonian operator
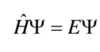
Give the Schrödinger equation for a particle of mass m moving in one direction with energy E
State some phenomena that are explained by quantum mechanics
- Photoelectron effect
- Atomic spectra
Give an equation for kinetic energy involving momentum
T = p2/2m
State the velocity of a free particle
Velocity is constant for a free particle
Give the equation for wavevector
Give the equation for angular momentum
Give the equation for wave velocity
Draw out the first 4 waves if a particle is confined to a box
State the position of nodes for a standing wave
Give and describe Wien’s displacement law
This law gives the observed shifts in the maximum of emission curves
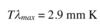
Give and describe the Stephan-Boltzmann law
M is the power emittance, ie rate of energy output
Give and describe the Rayleigh-Jeans law
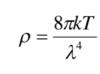
Describe the photoelectric effect and how it is an example of wave-particle duality
- When a metal is exposed to UV light, electrons are ejected from the metal’s surface
- Below a threshold frequency, no electrons are emitted
- Even at low intensities, electrons are emitted as long as threshold frequency is reached
- The kinetic energy of the electrons varies with frequency but not with intensity
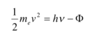
State the de Broglie relationship
Define the Hamiltonian operator
H = T + V
Hamiltonian operator = kinetic emergy operator + potential energy operator
Describe quantum tunnelling
Quantum tunnelling describes the phenomena of a subatomic particle being able to travel through a classically forbidden region. The particle’s behaviour can be explained by it having wavelike properties
V is the potential barrier, E is the energy of the particle, a is the thickness of the barrier in m
Describe Heisenberg’s uncertainty principle
“It is impossible to specify simultaneously with arbitrary precision, both the momentum and the position of a particle”
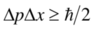
Describe cases in which quantum tunnelling is present in chemistry
- The oxidation and reduction of metals. When ligands are present, the transferred electrons seem to pass through them
- Electrical contacts. Metal surfaces are usually coated with a thin layer of oxide. Conduction can take place by tunnelling through this layer.
- Electrode reactions.
- Photon transfer
- Bond rotation
Describe the scanning tunnelling microscope
The microscope consists of an atomically sharp tip. A voltage is applied between the tip and the surface, ensuring they are very close but not touching so that tunnelling occurs
Give the momentum operator in 1 dimension
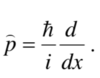
Give the Schrödinger equation for a free particle moving in 1 dimension
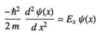
Give examples of a free particle
- A gas molecule in a big container
- An electron conducting in a metal
- An electron beam
Give the Schrödinger equation for a particle in a box
The particle is no longer free, although V inside the box is 0. Outside V is infinite - the particle cannot exist at or outside the walls as infinite energy is impossible.
Note: There are boundary conditions. Ψ at the edges of the box = 0
State the condition for a solution to the Schrödinger equation to satisfy
operator x function = constant x function
Describe the Born interpretation for Ψ
For a particle moving along x, the probability of finding a particle in a infinitesimally small region of space between x and x+dx is proportional to Ψ2.
The probability therefore must = 1
State what |Ψ|2 =
|Ψ|2 = Ψ*Ψ
State the properties of a well behaved wavefunction
- Single valued, as a particle can only have one probability at a certain point
- Finite
- Continuous
- Not equal to 0 everywhere
Give the Schrödinger equation for a simple harmonic oscillator
Potential energy has a value.
k is the spring constant
m is the reduced mass of the system
Describe the Schrödinger equation for a particle on a ring
We must consider angular momentum.
The boundary condition is that the number of wavelengths must be an integer, otherwise, there will be interference
V = 0 and r, the radius, is constant
