Quantum chemistry- Core 1

Question 1

Name the different parts of Bohr atom as shown on the picture.

What are properties of this model?

Answer 1

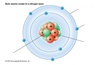
Going clockwise:

Energy level (shell)

An electron (on an orbit)

Neutron (in a nucleus)

Proton (in a nucleus)

Electron behaves as a particle and position is predictable.

Question 2

What is mass number?

Answer 2

Number of protons + number of neutrons

Question 3

What is atomic number?

Answer 3

Atomic number is number of protons. It also equals to number of electrons as atom is neutral overall.

Question 4

Give relative masses and charges for:

proton, electron, neutron

Answer 4

Proton:

Relative mass: 1

Relative charge: +1

Neutron:

Relative mass: 1

Relative charge: 0

Electron:

Relative mass: 1/1840

Relative charge: -1

Question 5

What determines the chemical properties of an element?

Where do elements with similar chemical properties are usually found?

Answer 5

Chemical properties are determined by electron configuration, so number of electrons in an outer shell.

Elements with similar properties are found in the same group of periodic table.

Question 6

What is the order of filling orbitals?

Answer 6

Question 7

What is the difference between a photon and a wave?

Answer 7

A wave is a means of transfer of energy between 2 points without there being any transfer of matter.

A photon is a particle and it is a quanta of energy (discrete packet of energy).

Question 8

Give me equation relating speed, frequency and wavelength

Answer 8

c=fλ

c= speed of light (3x10^8 m/s)

λ= wavelength (m)

f= frequency (s^-1)

Question 9

What is frequency?

Answer 9

The amount of times our wave passes through a point in one second.

Question 10

What is the wavelength?

Answer 10

wavelength is the distance between two consecutive troughs or two consecutive peaks.

Question 11

Give an equation for energy of a photon.

Answer 11

Question 12

What are the ranges of wavelengths for each type of light in EM spectrum?

Answer 12

Question 13

What is spectroscopy all about?

Answer 13

Shining light at a substance and then analysing the light that was absorbed or that comes out.

You get a spectrum.

Question 14

How is absorption spectrum done?

Answer 14

Gas is heated up and then photons of different wavelengths are emitted as electrons go back to their ground states.

You get series of thin lines on black background.

Question 15

How is absorption spectrum obtained?

Answer 15

gas is cooled down and then light passes through a substance. Absorption spectrum shows which frequencies of light were absorbed against a broad range of electromagnetic spectrum.

Question 16

Describe what is meant by quantization of energy levels?

Answer 16

Energy levels are quantized which means that only discrete frequencies can be absorbed or emitted by an atom, which is backed up by having only a few lines recorded on emission or absorption spectra.

Only certain photons excite or de-excite electrons to higher or lower energy levels respectively.

Question 17

What is rydberg equation? What is it used to describe?

Answer 17

v= R_H (1/n²₁- 1/n₂² )

v= frequency (s^-1)

n1, n2= lower energy level and higher energy level

It is used to classify energy difference for every line in

H- EMISSION SPECTRUM

Question 18

Describe to me wave-like behaviour of an electron in the atom.

Answer 18

• objects that are small can display wave-like properties.
• This is as a consequence of de Broglie equation where sufficiently small mass can produce significant wavelength to observe these properties.
• electrons are spread out and we can’t easily predict their position. We can only use probabilities that they can be found in a volume of space known as orbita.

Question 19

What is a standing wave? What is the requirement to produce standing wave in an atom?

Answer 19

A standing wave is a stable wave where it interferes with itself constructively. Whole number of wavelengths needs to fit around the circumference of an orbit to produce this stable wave

Question 20

Give me propreties of waves and describe what are these properties?

Answer 20

Difrraction- when a wave passes through a slit or obstacle, it spreads out. The effect is at its highest if wavelength is similar to the size of an obstacle

Refraction- the wave changes speed after it passes between media with different densities which often results in change in direction

Reflection- a wave bounces off a medium and travels in the opposite direction in the same medium.

Interference- the overall displacement of two waves at a point equals to the vector sum of their individual displacements at a point. They can interfere constructively or destructively.

Question 21

What is a wavefunction?

Answer 21

A wavefunction describes how an electron wave behaves with position and direction. It is solution to the SchrÖdinger equation.

Question 22

What is the Bohr interpretation of a wavefunction?

Answer 22

Bohr interpretation of a wavefunction states that if we square a wavefunction at a point in space, it will give us probability of finding an electron at that point in space.

If it is high, the probability is high, if it is low it is quite unlikely.

Question 23

What is de Broglie equation? Which quantities does it relate?

Answer 23

The de Broglie equation relates wave-like properties (wavelength) to particle like properties (momentum). If particle is sufficiently small in mass, its wavelength will be significant to display wavelike properties

Question 24

State the Heisenberg uncertainty principle and describe what does it show?

Answer 24

It shows that for a qunatum particle, if we know its momentum (energy) quite well, then we have a large uncertainty in position and we can’t predict it accurately.

Question 25

Give me the solution for a Schrodinger equation that predicts energy levels in a hydrogen atom or (hydrogen like atom). Describe what each element in the equation represents.

Answer 25

Rh is rydberg constant which relates to energy of our levels. (see rydberg equation)

Z2 takes into acount that the larger the nuclear charge, the larger the attraction is.

n is principal quantum number and it relates to size and energy of an energy level. It is qunatized so energy levels are also quantized

Question 26

Give definition of: ground state, de-excitation and excitation.

Answer 26

Ground state is the lowest, most stable energy state for an electron

Electron can be excited to higher energy level by absorbing the photon

Electron can be de-excited by releasing a photon and dropping to ground state.

Question 27

What is an atomic orbital? How are pictures of atomic orbitals obtained?

Answer 27

An atomic orbital is the region of space where it is most probable to find an electron.

For chemists, rather than using mathematical wavefunction, it is more useful to square it at each point in space to get a pictorial representation of probabilities of finding an electron. These are known as boundary surface representation.

Question 28

What does electron density plot show us?

Answer 28

The density of dots at each point in space shows us the probability of finding an electron at that point in space.

Question 29

State the properties of S-orbital.

Answer 29

• it is spherically symmetrical (wavefunction varies with distance only)
• it is spherical in shape
• as we get higher in energy, we get more structure to it
• no nodal planes
• radial nodes
• nucleus is at the centre.

Question 30

State the properties of p orbitals.

Answer 30

• dumbbell shape
• lobes have different amplitudes
• nodal plane through a nucleus
• we get some radial nodes as structure gets more complex
• three p orbitals: px, py, pz they are identical, just face in different directions.

Question 31

State the properties of d orbitals.

Answer 31

• they have two nodal planes
• radial nodes as structure gets more complex. Cone node in case of dz^2
• shapes as below
• lobes facing opposite have same amplitude.

Question 32

What are 3 different quantum numbers? What do they represent?

Answer 32

n- principal quantum number. It shows energy and size of an orbital

l- angular momentum quantum number. It shows shape of an orbital

ml- magnetic quantum number. It shows the direction that each orbital faces.

Question 33

What do quantum numbers govern? You can provide equations

Answer 33

For n shell:

n-1= number of different l’s

eg n=4 l=0,1,2,3

(-l) - (l)- number of different ml values

eg l=2 ml=-2,-1,0,1,2

Quantum numbers govern which sub-shells are allowed within each energy level and how many electrons each energy level can hold.

Question 34

for l=0,1,2,3, which subshells does each correspond to?

Answer 34

l=0 s-subshell

l=1 p-subshell

l=2 d-subshell

l=3 f-subshell

Question 35

What is radial wavefunction?

Give characteristsics of radial wavefunction.

Answer 35

Radial wavefuntion shows how wavefunction varies with distance from thhe nucleus.

For most wavefunctions, at r=0 radial wavefunction is also 0. The only exception is for s orbital which is going to have positive value of wavefunction

each wavefunction dies out when distance r increases as they have 1/e^r dependency. Wavefunction gets infinitesimally small and never reaches 0.

Question 36

How are nodes calculated in radial distribution function?

Answer 36

of nodes= n-l-1

They are the points where wavefunction equals 0 i.e the probability of finding an electron at that point is 0.

Question 37

what parts does the wavefunction consist of?

Answer 37

Ψ= K x R(r) x A(θ,ϕ)

K= normalising factor

R(r)= radial wavefunction- how it varies with r distance from nucleus. Tells us about energy and size.

A(θ,ϕ)= angular wavefunction, how it varies with changing angle. Tells us about shape.

Question 38

What is radial distribution function? Why is it a better representation of an atom than radial wavefunction?

Answer 38

Radial distribution wavefunction is the probability of finding an electron within a small volume of spherical shell with surface area 4πr², r distance away from the nucleus.

radial distribution wavefunction= 4πr²R(r)²(dr)

It is better representation because it captures all the points that are r distance away from the nucleus in a shell rather than a single point r distance away from the nucleus. That is why our most probable distance, Bohr radius is further from the nucleus because the bigger the shell, the more electron density dots it captures and the higher the probability.

Question 39

What is bohr radius?

Answer 39

the most probable distance of finding an electron in a hydrogen atom in its ground state (lowest energy state).

Question 40

What is an orbital approximation?

Answer 40

Orbital approximation is a way of obtaining an overall wavefunction for N-electron atom. It is obtained by multiplying individual wavefunctions for a hydrogen atom by each other.

This is done because we can only solve Schrodinger equation accurately for a 2 body problem.

Question 41

What is shielding?

Answer 41

It is the screening of outer electrons by inner electrons. Because of repulsions between core electrons, valence electrons do not experience full nuclear charge (only Zeff) and attractions are weaker.

Question 42

What is an orbital penetration?

Answer 42

A phenomena where electron in one orbital spends more time closer to the nucleus than for the other orbital, experiencing stronger attractions and lower shielding. This is observed because our radial distribution functions have different shapes.

Question 43

State Pauli’s exclusion principle

Answer 43

each orbital can hold a maximum of two electrons which have opposite spins

Question 44

State Hund’s rule

Answer 44

Degenerate orbitals fill singly before pairing starts as electrons repel each other.

Question 45

State Aufbau principle.