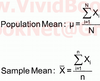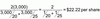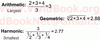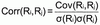Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

CFA: Level 1 > Quantitative Methods: Basic Concepts > Flashcards

Quantitative Methods: Basic Concepts Flashcards

1
Q

TVM: Interpreting Interest Rates (3)

A
  • Equilibrium interest rates are required rate of return for a particular investment
  • Interest rates also known as discount rates
  • Interest rates are the opportunity cost of current consumption because future consumption could be i% higher
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

TVM: Components of Interest Rates

A

Required (nominal) interest rate on a security=

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

TVM: Effective Annual Rates - Examples (3)

A

Stated Annual Rate is 12%

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

TVM: TVM - Example (2)

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

TVM: PV of a Perpetuity - Example

A

Preferred stock pays $8/year forever, with 10% rate of return. What is it’s present value?

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

TVM: FV of Single Sum

A

FV of $200 invested for 2 years at 10% interest rate

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

TVM: PV of a Single Sum - Example

A

PV of $200 in 2 years at 10% interest

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

TVM: PV of an Ordinary Annuity

A

PV of $200, received each year, for 3 years, at 10% interest rate

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

FV of an Ordinary Annuity

A

What is the value in three years of $200 to be received at the end of each year for three years when interest rate is 10%

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

TVM: PV of Annuity Due

A

PV of $200 received at the start of each year, for 3 years at 10%

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

TVM: FV of Annuity Due

A

FV of $200 received at beginning of each year for 3 years at 10% interest

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

TVM: FV of Uneven Cash Flows

A

PV of $300 received 1st year, $600 received 2nd year, and $200 received 3rd year at 10% interest

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

TVM: PV of Uneven Cash Flows

A

PV of $300 received 1st year, $600 received 2nd year, and $200 received 3rd year at 10% interest

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

TVM: Mortgage Example

A
  1. Month Payment on $100K, 30-year home loan at 6% stated rate N=30y x 12m = 360 payments, I = 6%/ 12m= .5 I/Y

PV= 100,000; FV = 0; CPT –>PMT = -599.55

  1. Remaining principle after 85 payments

N = 360 - 85 = 275 payments left CPT –> PV = 89,488

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

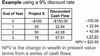
DCF: NPV

A

Net present value: the sum of present values of a series of cash flows

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

DCF: IRR

A
  • Internal rate of return: IRR is the discount rate that equates the PV of a series of cash flows to their cost
  • The IRR is the discount rate that makes NPV = 0
  • Possible Problems with IRR:
    • When a series of cash flows goes from negative to positive, then back to negative again, there can be more than one IRR
    • Series of csh flows can be ranked by their NPVs, but IRR rankings can differ
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

DCF: Holding Period Return: Example

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

DCF: Time-Weighted Returns

A

Annual time-weighted returns are effective annual compound returns

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

DCF: Money-Weighted Returns

A
  • Money-weighted returns are like an IRR measure
  • Periods must be equal length, use shortest period with no significant cash flows
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

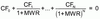
DCF: BDY, HPY, EAY, MMY

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

DCF: Yield Example

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

DCF: BEY

A

Bond Equivalent Yield is 2x the effective semi-annual yield

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

Statistics: Basic Terms (7)

A
  1. Descriptive Statistics- describes properties of a large data set
  2. Inferential Statistics- use a sample from a population to make probabilistic statements about the characteristics of population
  3. Population- a complete set of outcomes
  4. Sample- a subset of outcomes drawn from a population
  5. Parameter- describes a characteristic of a population
  6. Sample Statistic- describes a characteristic of a sample (drawn from a population
  7. Frequency Distribution- a table that summarizes a large data set by assigning the observations to intervals
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

Statistics: Measurement Scales (NOIR) (4)

A
  1. Nominal- Only names make sense (eg. Parrot, robin, seagull)
  2. Ordinal- Order makes sense (eg. large-cap, mid-cap, small-cap)
  3. Interval- Intervals make sense (eg. 40F is 10* greater than 30F)
  4. Ratio- Ratios make sense (abs zero) (eg. 200 is 2x as $100)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

Statistics: Frequency

A
  1. Relative Frequency Distribution- shows a percentGe of a distribution’s outcomes in each interval
  2. Cumulative Frequency Distribution- shows the percentage of observations less than upper bound of each interval
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

Statistics: Histogram

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

Statistics: Frequency Polygon

28
Q

Statistics: Population and Sample Means

A

Population and Sample means are both arithmetic means but have different symbols.

29
Q

Statistics: Geometric Means (3)

A
  1. Geometric mean is used to calculate periodic compound growth rates
  2. If the returns are constant over time, geometric mean equal arithmetic mean
  3. The greater the variability of returns over time, the more the arithmetic mean will exceed the geometric mean

Actually, the compound rate of return is the geometric mean of the price relatives, minus one

30
Q

Statistics: Geometric Mean - Example

A

Investment account had returns of +50% over the first year and returns of -50% over the second year. Calculate avg. ann. cpd ror

31
Q

Statistics: Weighted Mean

A

A mean in which different observations have different proportional influence on the mean.

32
Q

Statistics: Harmonic Mean

A

Used to find the average cost per share of stocks purchased over time in constant dollar amounts

33
Q

Statistics: Harmonic Mean - Example

A

Investor buys $3000 stock at $20 month 1, and $3000 stock at the end of month 2 at $25. What is the average cost per share of stock?

34
Q

Statistics: Calculating Means - Example (3)

A

Calculate arithmetic, geometric, and harmonic means of 2, 3, and 4

35
Q

Statistics: Portfolio Return - Example

36
Q

Statistics: Median

37
Q

Statistics: Mode

38
Q

Statistics: Quantiles

39
Q

Statistics: Range and MAD (2)

A

Annual returns data: 15%, -5%, 12%, 22%

  • Range: the difference between the largest and smallest value in a data set = 22% - (-5) =27%
  • Mean Absolute Deviation: Average of the absolute value of deviations from the mean
40
Q

Statistics: Population Variance and Standard Deviation (2)

A
  • Variance- the average of the squared deviations from the mean
  • Standard deviation: is the square root of the variance
41
Q

Statistics: Sample Variance (s2) and Sample Standard Deviation (2)

42
Q

Statistics: Chebyshev’s Inequality

A

Specifies the minimum percentage of observations that lie within k standard deviations of the mean; applies to any distributions with k>1

43
Q

Statistics: CV

A
  • Coefficient of Variation
  • A measure of risk per unit of return
44
Q

Statistics: Sharpe Ratio

A
  • Excess return per unit of risk; higher is better
  • Sharpe ratio = mean return - risk free rate/ standard deviation
45
Q

Statistics: Skewness (8)

A
  • Skew measures the degree to which a distribution lacks symmetry
  • A symmetrical distribution has skew = 0
46
Q

Statistics: Positve Skew = Right Skew

47
Q

Statistics: Negative Skew = Left Skew

48
Q

Statistics: Kurtosis

A
  1. Measures the degree to which a distribution is more or less peaked than normal distribution.
  2. Leptokurtic (kurtosis > 3) more peaked and fatter tails (more extreme outliers)
  3. Kurtosis for a normal distribution is 3.0
  4. Excess kurtosis
    • Excess kurtosis is kurtosis minus 3
    • Excess kurtosis is 0 for a normal distribution
    • Excess kurtosis greater than 1 in absolute value is considered significant
49
Q

Statistics: Mean Investment Returns- Example (3)

50
Q

Probability: Terminology (5)

A
  1. Random Variable: Uncertain number
  2. Outcome: Realization of random variables
  3. Event: Set of one or more outcomes
  4. Mutually exclusive: cannot both happen
  5. Exhaustive: Set of events includes all possible outcomes
51
Q

Probability: Properties

52
Q

Probability: Types (3)

A
  1. Empirical: Based on analysis of data
  2. Subjective: Based on personal perception
  3. A priori: Based on reasoning, not experience
53
Q

Probability: Odds for or Against (2)

A

Odd happening/ odds not happening.

Given probability that a horse will win a race= 20%

  • Odds for:.20/ (1-.2)= .2/.8= 1/4 or 1 to 4
  • Odds against (1-.2) .2= .8/.2= 4 or 4 to 1
54
Q

Probability: Conditional vs Unconditional (2)

A

Two types of probability:

  • Unconditional P (A), the probability of an event regardless of the outcomes of other events
  • Conditional P (A|B), the probability of A given that B has occurred (e.g. The probability that Marley will be up, given the red raises interests rates)
55
Q

Probability: Rules (4)

56
Q

Probability: Joint

A
  • The probability that both events will occur is their joint probability
  • Examples using conditional probability:
    • P (interest rates will increase) = P (1) = 40%
    • P (recession given a rate increase) = P (R|I) = 70%

Probability of a recession and an increase in rates,

  • P (RI) =P(R|I) x P(I) =.7 x .4 = 28%
57
Q

Probability: At least one of two events will occur (2)

A
  • P (A or B) = P(A) + P(B) - P(AB)
  • We must subtract the joint probability P (AB)
58
Q

Probability: Additional Rule - Example

A
  • Prob (I) = probability of rising interest rates is 40%
  • Prob (R) = probability of recession is 34%
  • Joint probability P (RI) = .28

What is the probability of either rising interest rates or recession?

P (R or I) = P(R) + P (I) - P(RI) = .34 +.40 - .28 = .46

Mutually Exclusive events the joint probability P(AB) = 0 so P (A or B) = P(A) + P(B)

59
Q

Probability: Joint Probability of any number of Independent Events (2)

A
  1. Dependent Events: Knowing the outcome of one tells something about the probability of the other
  2. Independent Events: Occurrence of one event does not influence the occurrence of the other. For the joint probability of independent events, just multiply

Example: Flipping a fair coin, P (heads) = 50% The probability of three heads in succession is .5 x .5 x .5 = 12.5%

60
Q

Probability: Calculating Unconditional Probability

A

P (Interest Rate increase) = P(I) = .4

P (No interest rate increase) = P(Ic) = 1 - .4 = .6

P (Recession | Increase) = P(R|c) = .70

P (Recession | No Increase) = .1

What is the unconditional probability of recession?

P(R)=P(R|I) x P(I) + P(R|Ic) x P(Ic) =.70 x .40 + .10 x .60 = .34

61
Q

Probability: Covariance

A

Covariance: a measure of how two variables move together

  • Values range from minus infinity to plus infinity
  • Units of Covariance are difficult to interpret
  • Covariance is positive when the variables tend to be above their expected values at the same time

For each observation, multiply each probability by the product of the two random variable’s deviation from the mean, and sum them

62
Q

Statistics: Correlation (4)

A

Correlation: A standardized measure of the linear relationship between two variables

Values range from +1, perfect positive correlation, to -1, perfect negative correlation

r is sample correlation coefficient

p is population correlation coefficent

63
Q

Statistics: Correlation - Example

A

(1) The covariance between two assets is .0046, õA is .0623 and õB is .0991. What is the correlation between the two assets?

64
Q

Statistics: Portfolio Expected Return

A

Expected return on a portfolio is a weighted average of the returns on the assets in the portfolio where the weights are proportional to portfolio value.

65
Q

Statistics: Factorial for Labeling - Example

A

Out of 10 stocks, 5 were rated to buy, 3 will be rated hold, and 2 will be rated sell. How many ways are there to do this?

66
Q

Statistics: Choosing r Objects from n Objects

A
  • Combination: When order does not matter and with two possible labels, we can use the combination formula. nCr = n! / (n - r)!r! = 5!/(5-3)!x 3! = 10
  • Permutation:You have 5 stocks and want to place orders to sell 3 of them. How many different combinations of 3 stocks are there? nPr = n! / (n - r)! = 5! (5 - 3)! = 60

CFA: Level 1 (18 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions