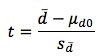Quantitative Methods Flashcards

Question 1

Q

Quantitative Methods

Interest Rates

Three ways to interpret interest rates

Answer

A

Required rate of return
Discount rate
Opportunity cost

Question 2

Q

Quantitative Methods

Interest Rates

3 components of interest rates

Answer

A

Risk free rate
Inflation
Default risk

Question 3

Q

Quantitative Methods

Interest Rates

Periodic interest rate

Answer

A

Simple rate of interest over a single compounding period

e.g. interest rate of 1.5% per quarter

Question 4

Q

Quantitative Methods

Interest Rates

Stated annual interest rate

Answer

A

= quoted interest rate

Annual rate ignoring compounding e.g. 4 * quarterly interest rate

Question 5

Q

Quantitative Methods

Interest Rates

Effective annual rate (EAR)

Answer

A

Annual interest rate taking into account compounding

Question 6

Q

Quantitative Methods

What is an “annuity due”?

Answer

A

Annuity with first payment at T0 (so last payment at T(n-1)

Question 7

Q

Formula: FV of annuity

Question 8

Q

IRR Problems

Answer

A

1 - Reinvestment Problem

2 - Scale Problem

3 - Timing Problem

Question 9

Q

IRR Problem 1

Reinvestment Problem

Answer

A

Assumes that all cash flows can be reinvested immediately at the IRR rate.

Question 10

Q

IRR Problem

2 Scale Problem

Answer

A

IRR ignores the scale of the return unlike NPV which would prioritise larger cash returns with the same IRR.

Question 11

Q

IRR Problem 3

Timing Problem

Answer

A

In the case where two projects have differing cash flow profiles (big cash flows early or late) IRR comparison is not useful.

Question 12

Q

Definition: Holding Period Return (HPR)

Answer

A

aka Total Return

This is the total return over a given period, including capital and distributions.

Question 13

Q

Dollar Weighted Rate of Return

Answer

A

Basically the IRR of an investment, taking amount and timing of cash flows into account.

So investing more cash when portfolio value is low leads to positive return, even if portfolio performance over the whole period is unchanged.

Thus a measure of what you earned from investing in the portfolio over the period, not a measure of the performance of the portfolio itself.

Question 14

Q

Time Weighted Rate of Return

Answer

A

The compound growth rate of $1 invested in the portfolio over the period. Ignores timing of cash flows (ie purchase/sale of portfolio) so is appropriate for measuring portfolio performance.

Simply calculate the return for each period (divs and share price movement) and then annualise.

Question 15

Q

Money Market Instruments

Bank Discount Yield

Definition and formula

Answer

A

This is the basis on which money market instruments are quoted.

Discount = FV - price you pay

t = Time to maturity

Question 16

Q

Money Market Instruments

4 money market interest rates

Answer

A

Holding Period Yield (HPY): simple periodic rate, just discount/FV or (FV-PV)/PV
Bank Discount Yield: Odd simple annualised rate used for money market, (discount/FV) * (360/t)
Money Market yield (r_m): Simple annualised yield, 360 basis, =HPY * 360 / t
Effective Annual Yield: Proper compound annual yield, = (1+HPY)^365/t - 1

Question 17

Q

Money Market Instruments

Bank Discount Yield

Issues with them

Answer

A

Based on the FV instead of purchase price, return should be measured off purchase price
Annualised of 360 days instead of 365
Annualised with simple interest, ignores value of compounding

Question 18

Q

Money Market Instruments

Holding Period Yield

Answer

A

Total return earned if held to maturity (not annualised).

Question 19

Q

Money Market Instruments

Effective Annual Yield

Answer

A

The annualised HPY based on 365 day year, annualised.

Question 20

Q

Money Market Instruments

Money Market Yield

aka?

definition

calculation from BDY

Answer

A

a.k.a. CD equivalent yield

Annualised HPY using simple interest on 360 day basis. (HPY = holding period yield).

r_mm= HPY * 360 / t

From BDY:

Question 21

Q

Bonds

Bond Equivalent Yield

Answer

A

Bond yields (in the US) typically quoted semi-annually. This method just doubles it (ignoring compound interest) to get an annualised yield.

So DON’T compare an annual yield bond to the BEY of a semi-annual yield bond.

Question 22

Q

Statistics

Definition of Parameter

Answer

A

A characteristic (value) of a population (not of a sample), denoted by greek letter.

For example the mean.

In investments, examples inlcude mean return and standard deviation of returns.

Question 23

Q

Statistics

Definition of a Statistic

Answer

A

An estimate of a parameter of a population, taken from a sample of that population.

Question 24

Q

Statistics

Definition of Inferential Statistics methods

Required qualities of the sample

Answer

A

Inferential Statistical Methods are used to draw conclusions about a large group based on a sample taken.

Require the sample to be either random or representative in different cases.

Question 25

Q

Statistics

Measurement

Definition of Nominal Scale

Answer

A

Assigning items to groups or categories, such as race or sex, qualitative rather than quantitative.

No ordering or ranking implied, but can allocate numbers to the groups (eg, 1 - value funds, 2 - growth funds).

Question 26

Q

Statistics

Measurement

Definition of Ordinal Scale

Answer

A

Allocated to each item a ranking for a certain characteristic (eg scale of 1 to 10 between worst and best performing manager).

There is an ordering implied but the scale is arbitrary and distances between the ranks not necessarily consistent.

Question 27

Q

Statistics

Measurement

Definition of Interval Scale

Answer

A

Items in population given a ranking for a certain characteristic, where an order is implied and the distance between each rank is standardised. Such that the difference between 0 and 10 is the same as 20 to 30.

However no zero point is defined therefore doubling from 10 to 20 is not the same as doubling from 20 to 40.

Question 28

Q

Statistics

Measurement

Definition of Ratio Scale

Answer

A

Ranking of items within a population on a given parameter, which has an ordering, where difference between each ranking is standardised and there is a defined zero point. So the effect of doubling from 10 to 20 is the same as from 20 to 40.

e.g. temperature on the Kelvin scale (NOT farenheit since the zero point in farenheit is arbitrary)

Question 29

Q

Statistics

Measurement

Order of Strength of the Scales

Answer

A

N - Nominal

O - Ordinal

I - Interval

R - Ratio

Question 30

Q

Statistics

Frequency Distributions

Definition of Absolute Frequency

Answer

A

Number of actual observations in a given interval.

Question 31

Q

Statistics

Frequency Distributions

Definition of Relative Frequency

Answer

A

The result from dividing the absolute frequency of a return interval by the total number of observations.

Question 32

Q

Statistics

Frequency Distributions

Definition of Cumulative Absolute Frequency

and

Cumulative Relative Frequency

Answer

A

Result of cumulating the results form absolute and relative frequency as you move from one interval to the next.

Question 33

Q

Statistics

Measures of Central Tendency

Definition of Geometric Mean

3 characteristics

Answer

A

See formula.

Used when calculating returns over multiple periods
Exists only if all values are greater than zero
Always less than arithmetic mean unless numbers are all the same (in which case they’re the same)

Question 34

Q

Statistics

Measures of Central Tendency

Definition of Harmonic Mean

Special cases with 2 or 3 numbers

Answer

A

Special cases also given:

H(x₁,x₂) = 2x₁x₂ / (x₁ + x₂)

H(x₁,x₂,x₃) = 3x₁x₂x₃ / (x₁x₂ + x₂x₃ + x₁x₃)

Question 35

Q

Statistics

Median - ‘iles

Examples

Inter-quartile range

Answer

A

There are 3 quartiles, 4 quintiles, 9 deciles and 99 percentiles in a data set
They split the population into 4, 5, 10 and 100 groups
Q₁ is the first or lowest quartile, Q₃ the highest
Distance from Q₁ to Q₃ is the inter-quartile range

Question 36

Q

Statistics

Deviation

Range

Answer

A

Difference between the lowest and higest values in a population of numbers.

Question 37

Q

Statistics

Deviation

Mean Absolute Deviation

Answer

A

Take the absolute difference between each value and the mean, then take the average of those results.

Question 38

Q

Statistics

Deviation

Variance (for a population)

Answer

A

This is the average squared deviation of each value from the mean.

Question 39

Q

Statistics

Deviation

Variance (for a sample)

Answer

A

Same as population, average of squares of difference between values and the sample mean.

Dividing by n results in a baised estimator of population variance, using n - 1 gives an unbaised estimator.

Question 40

Q

Statistics

Deviation

Standard Deviation

1sd and 2sd bands

Answer

A

Simply the square root of the variance.

Normal distn - 68% within 1 sd, 95% within 2 sd.

Standard Deviation not directly comparable between different data sets since means are different sizes (not a relative measure).

Question 41

Q

Statistics

Deviation

Coefficient of Variation

Answer

A

A relative dispersion measure, so allows comparison between different data sets.

Simply divide standard deviation by the mean.

a.k.a. Relative Standard Deviation

Question 42

Q

Statistics

Chebyshev’s Theorem

Answer

A

For any sample/population, the proportion of observations within c standard deviations of the mean is at least 1 - 1/c².

Works on sample and population, discrete or continuous data.

Allows us to measure minimum amount of dispersion from the standard deviation.

Question 43

Q

Statistics

Sharpe Measure

Answer

A

r_p= mean return of portfolio

r_f = risk free mean return

σ_p = standard deviation of portfolio

a.k.a. reward to variability ratio

Measures the reward to volatility trade-off and recognises the existence of a risk-free return.

Question 44

Q

Statistics

Skewness

Definition

Value for normal distn

Answer

A

The degree of asymmetry of a data set.

Normal distribution has zero skewness.

Positively Skewed Distribution means a long tail to the right (a few big wins, lots of small losses). Also say skewed to the right.

Question 45

Q

Statistics

Skewness

Where are mean, median and mode when skew is positive?

Answer

A

Mode: The peak of the distribution.

Mean: Pulled towards the long tail (extreme values).

Median: In-between.

Question 46

Q

Statistics

Skewness

Formula

Conditions for calculation to be valid

Answer

A

Valid when N is large.

Zero for normal distribution.

Question 47

Q

Statistics

Kurtosis

Definition

Answer

A

Measure of how much a distribution is stretched out to the tails or peaked around the mean, regardless of skew.

Normal distribution has a neutral kurtosis.

Question 48

Q

Statistics

Kurtosis

Words for types of kurtosis

Answer

A

Platykurtic: Low peak, more returns with large deviations from the mean.
Leptokurtic: Tall peak, few returns with large deviations from the mean.
Mesokurtic: Same kurtosis as normal distribution.

Question 49

Q

Statistics

Kurtosis

Formula

Answer

A

Formula is for excess kurtosis.

Normal distribution has kurtosis of 3 and excess kurtosis of 0.

Question 50

Q

Probability

Empirical Probability

Answer

A

A probability based on frequency of occurence in a set of historical data.

Question 51

Q

Probability

Priori Probability

Answer

A

A probability based on logical analysis rather than historical observation (eg 50% chance of heads on coin toss).

Question 52

Q

Probability 3

Subjective Probability

Answer

A

A probability based on subjective judgement (eg John thinks there is a 60% chance of a merger occuring). Priori and Empirical probabilities by contrast are considered to be objective.

Question 53

Q

Probability

Marginal Probability

Answer

A

Another name for unconditional probability, i.e. just the probability that an event will occur, NOT conditional on any other events having occured.

Question 54

Q

Probability

Independence of two events

Multiplication Rule

Answer

A

Means P(A) = P(A|B) or vice versa.

In this case P(AB) = P(A) * P(B) which is the multiplication rule.

Question 55

Q

Probability

Total Probability Rule

Answer

A

P(A) = P(A|S₁) + P(A|S₂) + … + P(A|S_n)

Where S₁ to S_n are mutually exclusive and exhaustive.

P(A) = P(A|S) + P(A|S^c)

Question 56

Q

Probability

Variance of a Random Variable

Answer

A

σ²(X) = E{ [X - E(X)]² }

Question 57

Q

Probability

Standard Deviation of a Random Variable

Answer

A

The positive square root of variance.

Question 58

Q

Probability

Covariance

Calculation

Answer

A

Cov( R_i, R_j) = E[( R_i - E( R_i ) ) * ( R_j - E( R_j ) )]

Note, covariance of a random variable with itself is:

Cov( R_i, R_i ) = E[( R_i - E( R_i ) )²]

i.e. it’s own variance

Question 59

Q

Probability

Correlation

Calculation for correlation between two returns

Answer

A

Divide covariance by the standard deviation of each random variable.

Question 60

Q

Probability

Expected return of portfolio

Expected variance of 2 member portfolio

(given means/variances of constituents)

Answer

A

Expected return is weighted average of individual returns.

Expected variance via formula below:

σ²(R_p) = w₁²σ²(R₁) + w₂²σ²(R₂) + 2w₁w₂Cov(R₁,R₂)

Question 61

Q

Probability

Bayes Formula

Answer

A

From total probablity rule:

P(X) = P(X|S) P(S) + P(X|S^c) P(S^c)

which gives us Bayes formula:

P(X|S) = P(X) * [P(S|X)/P(S)]

or

P(X|S) = [P(X)/P(S)] * P(S|X)

Question 62

Q

Probability

Combinations

Does order matter?

Formula

Answer

A

In Combinations order does NOT matter:

_nC_r = n! / (n-r)r!

Question 63

Q

Probability

Permutations

Does order matter?

Formula

Answer

A

For Permutations order DOES matter:

_nP_r = n! / (n-r)!

Question 64

Q

Distributions

Continuous Uniform Distribution

Describe

Probability density function

Cumulative density function

Mean

Variance

Answer

A

Equal probability (straight line) within a given range.

f(x) = 1/(b-a) for a<=x<=b

F(x) = (x-a) / (b-a) for a<=x<=b

µ(x) = (a+b)/2

σ²(x) = (b-a)²/ 12

Answer 64

A

An experiment with two possible outcomes (i.e. single experiment in a binomial distribution)

Answer 65

A

Binomial Random Variable B(n,p) is the number of successes in n bernoulli trials where probability of success in an individual trial is p.

Probability of r succeses in n trials is:

p(r) = _nC_r * p^r * (1-p)^n-r

µ(B(n,p)) = np

σ²(B(n,p)) = np*(1-p)

Answer 66

A

90% x-bar - 1.645σ to x-bar + 1.645σ

95% x-bar - 1.96σ to x-bar + 1.96σ

99% x-bar - 2.58σ to x-bar + 2.58σ

Answer 67

A

Z table is based on a normal distribution with mean 0 and standard deviation 1.

Z-value is therefore the number of standard deviations from the mean (z = (x - µ)/σ).

For a given potential outcome convert using the mean and SD of that test to a z value to find the probability of outcome being above/below that potential outcome.

Answer 68

A

Distribution of a group of random variables, in this case several normally distributed variables e.g. the distribution of a portfolio of normally distributed stock returns.

Dependent on means and standard deviations of individual stocks plus the correlation matrix.

Answer 69

A

Shortfall is risk that portfolio falls below an acceptable value.

Saftey First criterion is to choose a portfolio with the lowest possible probability of falling below this value.

For normal distribution this equates to maximising the SF-Ratio: SF Ratio = (E(R_P) - R_L) / σ_P

Where R_P is portfolio return, R_L is minimum return.

Answer 70

A

A random variable Y follows a lognormal distribution if it’s natural logarithm lnY is normally distributed.

So it’s lognormal if its log is normal.

Answer 71

A

Denoted by r_t,t+1 (cont. comp. rate of return between t and t+1):

r_t,t+1 = ln(S_t+1/S_t) = ln(1+R_t,t+1)

Gives a more reasonable average return as:

[(1.2/1 - 1) + (1/1.2 - 1)] / 2 = 2.5%

[ln(1.2/1) + ln(1/1.2)] / 2 = 0%

Answer 72

A

A sample that has been taken using a biased method, resulting in a sample with different characteristics than the population.

Note that a sample with different characteristics than the population as a result of randomness in a fair sample, is NOT a biased sample.

Answer 73

A

For a given sample size, and sample statistic (e.g. the sample mean), the sample distribution is the distribution of outcomes of that statistic across an infinite number of samples.

Alternatively it’s the relative frequency of outcomes of the statistic for every possible sample of the population, of the given sample size.

Answer 74

A

Split the population up into sub-populations based on given characteristics, then select a sub-sample from each with size based on relative size of the sub-population. Put the sub-samples together to get a sample of the population.

This ensures proportional representation across the characteristics used to split the population.

Answer 75

A

As opposed to time-series data, cross-sectional data consists of observations at a single point in time, such as the closing prices of 20 different stocks at close on a given date.

Answer 76

A

Given a distribution with mean µ and variance σ², the sampling distribution of the mean x-bar approaches a normal distribution with mean µ and variance σ²/N as the sample size (N) increases.

With N > 29 it is normal EVEN IF underlying distribution is not normal.

This allows us to construct confidence intervals on the population mean from sample data using normal distn., regardless of whether the population is normally distributed!

Answer 77

A

The standard error of a statistic is the standard deviation of the sampling distribution of that statistic.

σ_m = σ / sqrt(N)

Where σ_m is the standard error of the mean, σ is the standard deviation of the population and N is the sample size.

This DOES NOT require the pop distn to be normal.

Estimate using sample standard deviation (s) if population standard deviation (σ) is not known.

Answer 78

A

Unbaisedness: The estimators expected value (mean of its sampling distn) equals the parameter it is meant to estimate.

Efficiency: Estimator is efficient if no other unbaised estimator of the parameter value has a lower standard error.

Consistency: Means the standard error of the unbaised estimator approaches zero as sample size increases.

Answer 79

A

The single estimate of an unknown population parameter calculated as a sample mean is called the point estimate of the mean.

The formula used to calculate it is called the estimator.

Answer 80

A

Degree of confidence is 95%

Level of significance is 5%

20 and 40 are the lower and higher confidence limits

There is a 95% probability that the population mean lies between 20 and 40

Answer 81

A

If the variance is not known use t-distribution instead of z-distribution for confidence intervals (with t table based on N-1 degrees of freedom, where N is the sample size).

If the population is not normal make sure you have sample size of 30+.

If the sample size is very high using the z distn is usually ok.

Answer 82

A

Bias as a result of using somebody else’s results of empirical (historic data) analysis to guide your own analysis over essentially the same historical data.

Can be avoided by carrying out analysis on new data, although this is difficult in investment analysis because the set of historical data is limited.

Answer 83

A

Bias created as a result of finding forecasting models through extensive searches of databases to find patterns.

Highly likely when there is no economic justification for the pattern.

Can be avoided by testing models on a different set of data.

Answer 84

A

Caused when analysis is carried out on a data set that has excluded (e.g.) stocks that have gone bankrupt. The data has an upward bias since it excludes a section of the population which performed very poorly.

Answer 85

A

Bias caused based on the assumption that fundamental information was available at a point in time when it isn’t.

For example assuming that people know their earnings data in January for January, when they might not find out till March.

Usually results in upwards bias.

Answer 86

A

Where a conclusion drawn relates only to a particular time period which may make that conclusion time-specific.

Usually a problem if the time period is too short (eg covers only an economic upswing).

Also a problem if the time period is too long since fundamental economic structure may have changed.

Answer 87

A

Designated H₀ this is the hypothesis regarding the population (eg mean monthly income is $5000) which you desire to test.

It is either rejected or failed to be rejected, never accepted.

Answer 88

A

Designated H₁, this is the statement which is accepted if the sample data provides sufficient evidence that H₀ is false.

Answer 89

A

A test statistic is a number calculated from the sample whose value (relative to its probability distn) provides statistical evidence against the null hypothesis.

Typically of the form:

test statistic =

(sample statistic - H₀ parameter value) / Standard error of sample statistic

Answer 90

A

Chosen in testing, this is the probability that a null hypothesis which is true is rejected.

Designated by greek letter alpha.

Answer 91

A

The decision rule is the statement of the conditions under which H₀ is rejected or not.

The critical value (2 of them if two-sided) is the dividing point past which H₀ will be rejected.

The critical region is the area where if the test stat falls in it, we REJECT H₀.

Answer 92

A

Note: With n=1 the sample distribution of the mean is just the distribution of the population, so the below simplifies to the z value.

This usually follows the normal distn (central limit theorem) therefore:

Answer 93

A

Type one error is the when H₀ is true but is rejected.

Type two error is when H₀ is false but is not rejected.

Type one is more serious and is controlled via the level of significance (alpha), which is the probability of a type one error. Reducing alpha to reduce the risk of a type one error increases the risk of a type two error (probability designated as ß).

Can only reduce both alpha and ß by increasing sample size.

Answer 94

A

The probability of correctly rejecting a false null hypothesis (1-ß). If the power of an experiment is low there is a high chance of an inconclusive result.

Assumes that H₀ is false.

Answer 95

A

Instead of stating a decision rule, calculate the test statistic and the calculate the probability of getting a value more extreme than that (one or two-sided) assuming H₀ is correct.

This probability can be compared to alpha value to decide whether to reject H₀, but also provides extra information about how strong the rejection is.

Answer 96

A

Below formula is the test statisticfor the hypothesis that the difference between two population means is a given number (or zero, ie that they are the same).

Degrees of freedom are n₁ + n₂ - 2 if population variances are assumed to be the same.

Requires normal distribution

Answer 97

A

Used on differences between related data (eg before and after data, results for twins).

H₀ : µ_d = µ_d0

Where µ_d is the difference between the means and µ_d0 is some fixed value (typically zero).

Requires Normal distribution

Answer 98

A

d-bar is the sample mean of differences

Standard error for the sample mean of differences:

s_d-bar is s_d/sqrt(n)

Standard deviation of the differences:

s_d = sqrt( Σ(d_i - d-bar)² / (n-1) )

n-1 degrees of freedom

Note: This is basically just normal distn.

Answer 99

A

Subject is the testing of the differences between two means. Treatment depends on whether the two populations are related.

If the population is the same (eg before or after) or is some way dependent then it is paired testing.

If populations are different (typically also sample sizes will be different) it is independent.

Answer 100

A

Chi-squared statistic.

s² is the sample variance

σ₀² is the hypothesised value for σ²

Population MUST be random AND normally distributed

n-1 degrees of freedom (similar to t-distn)

Answer 101

A

Fischer distribution (F-distribution)

F = S₁² / S₂²

Convention states larger sample variance goes on top.

Requires both populations to be normally distributed.

Note that degrees of freedom are excluded since n₁-1 in both denominator and numerator.

Answer 102

A

F-distribution tables denoted by F(n₁ - 1, n₂ - 2) where n₁ and n₂ are sample sizes of numerator and denominator.

F-distribution is one-directional, H₀ is that σ₁² <= σ₂² because we chose 1 & 2 such that s₁² > s₂². We then test whether the ratio is high enough to reject H₀.

For two-sided tests (H₀: σ₁² = σ₂²) need to halve alpha.

As with chi-squared, distn MUST be random AND normal.

Answer 103

A

This is testing of something other than a parameter of the population (such as mean or variance).

Parametric tests are preferred where relevant, but may not be due to the distribution of the data, nature of the data (eg ordinal/ranked data) or where no parameter is involved (eg testing whether data is indeed random).

Answer 104

A

Both agree that supply and demand control prices, however technical analysts believe this information feeds into prices gradually over a period of time and trends can be taken advantage of.

Answer 105

A

Xs represent upwards price trends and Os represent donwards trends.

X axis not linear in time, dependent on price movements. Chart switches between X’s and O’s when trend deemed to have shifted.

Answer 106

A

For upwards trends draw an upwards pointing support line below the low points.

For a downwards trend draw a downwards trending resistance line joining the peaks.

Answer 107

A

When a price breaks through a resistance line that same price level then becomes a support (or vice versa), referred to as a change in polarity.

Answer 108

A

Head and shoulders is a reversal pattern (as is inverse HaS).

Look for higher volume on the left shoulder rally than the head rally, increases in volume on the sell-offs.

Target price = neckline - (head peak - neckline)

Answer 109

A

Double (or triple) top/bottom is a reversal pattern characterised by the price hitting a support/resistance level twice and failing to break it.

Answer 110

A

Traingles are continuation patterns, either ascending (supported by ascending trend line, top is a flat resistance line), descending (descending resistance line with stock bouncing off a flat support line) and symmetrical (both support ascending and resistance descending).

The original pattern is expected to assert itself (ie the horizontal line for asc/desc is only temporary).

Answer 111

A

Horizontal support and resistance lines, ie rangebound. Can stay in the range for a while, but usually expect the trend before the pattern was established to eventually continue.

Answer 112

A

Short-term continuation patterns representing a consolidation for a short time.

A flag has parallel support and resistance lines in a different direction to the larger trend.

A pennant is a symmetrical triangle (ascending support, descending resistance) with a typically neutral overall slope.

Answer 113

A

When a short-term moving average breaks out above a longer-term moving average this is considered a bullish signal.

The opposite is a dead cross.

Answer 114

A

Measure the percentage price change over a given period (eg charts the % price change over the last 20 days).

Answer 115

A

Compares the average price change during advancing periods to average price change during declining periods.

RSI = 100 - 100/(1 + RS)

Where RS = average gain / average loss

RSI is a range of zero to 100 where above 70 considered overbought and below 30 considered oversold.

Answer 116

A

This is simply the level of the close expressed as a percentage between the lowest low and highest high in its current range (so at 50% it’s in the middle of its established range).

Answer 117

A

Simply the difference between a short and long term moving average, so when they converge the value is zero, and as the moving averages diverge the MACD becomes negative or positive.

Answer 118

A

Indicator that measures the extent to which money is moving into or out of rising or declining stocks.

Ratio of 1 means market is in balance.

Ratio > 1 means more money is moving into declining stocks.

Ratio < 1 means more money moving into advancing stocks.

Answer 119

A

Sinusoidal like waves which the world economy follows on a periodicity of 40 to 60 years.

Answer 120

A

States that the market isn’t random but moves in cycles.

Says the market moves in five waves of the prevaling trend (impulse waves) and three corrective waves which counter the trend.

The waves count is a Fibonnaci sequence.

Answer 121

A

Simply the practice of looking at several related markets at the same time to determine patterns (eg US bond market and US equity market).

Answer 122

A

HPR = 1 + HPY

Answer 123

A

Leptokurtic distributions have FAT tails.

Platykurtic distributions have more observations far away (so tails stretch further away) but observations in the tails less bunched together, so they look LONG and THIN.

Answer 124

A

Use Chebyshev’s equation to get confidence intervals based on # standard deviations for any distribution.

Answer 125

A

Amount of time since price change (along with % of income spent on the product and closeness of substitutes) impacts elasticity of demand.

Changes in price expectations shifts the aggregate demand curve to the left or right, but doesn’t impact elasticity of demand.

Answer 126

A

Backfill bias is when a new item is added to an index and performance from before the date of its addition is included in the index.

Brainscape's Knowledge GenomeTM

Quantitative Methods Flashcards

Brainscape's Knowledge Genome^TM