Quanta and Waves Flashcards
Considering the relationship shown for velocity in SHM, describe the conditions when the velocity is at a maximum and at a minimum.

Velocity is at a MAXIMUM when y = 0 (This simplifies the equation to vmax=ωA).
Velocity is at a MINIMUM (zero) when y = A or -A.
Assuming no energy losses, describe how the type of energy an object undergoing simple harmonic motion has changes over time.
The energy of the object is constantly being converted from kinetic energy to potential energy and back again.
Kinetic energy is at a maximum when velocity is at a maximum (at y=0).
Potential energy is at a maximum when velocity is zero (when y = A or -A)
At any point:
total energy = potential energy + kinetic energy.
Classical theory suggested that as an object becomes hotter, the irradiance of short wavelength radiation would increase dramatically. In fact, experiements show this irradiance is very small.
What is this effect known as, and why does it happen?.

- This is known as the ‘ultraviolet catastrophe’.
- The reason it happens is because individual photons have their energy quantised by the relationship E=hf.
- Due to energy conservation, there are far less high energy photons allowed than at other wavelengths.
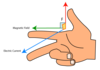
The direction of the force exerted on a negatively charged particle entering a magnetic field perpendicularly can be determined using the ‘right hand rule’.
Describe the use of the ‘right hand rule’ by determining which ‘finger’ represents which quantity.
State the Heisenberg uncertainty principle.
Heisenberg’s uncertainty principle states that the precise position of a quantum particle and it’s momentum cannot both be known at the same instant.
The de Broglie wavelength of a particle can be considered to be the same as the uncertainty in its position (Δx).
Considering this, explain what conditions are required to create diffraction patterns from beams of particles by a double slit.
The distance between the slits needs to be approximately equal to, or smaller than, the particle’s de Broglie wavelength, as there is an uncertainty to which slit the particle will travel through.
If the slits are a greater distance apart, the particles will only pass through one slit and no diffraction pattern will be observed.
State what is meant by an object undergoing ‘simple harmonic motion’.
The restoring force (on the object) is directly proportional to, but opposite in direction to, the object’s displacement from its equilibrium position.
Describe the motion of a charged particle which enters a magnetic field:
- Perpendicular to the field
- Parallel to the field
- At an angle
- The particle will travel with circular motion only.
- The particle will continue with linear motion parallel to the field only.
- The particle will travel with helical motion (circular perpendicular to the field and linear parallel to the field).
By referring to the uncertainty principle relating energy and time, explain the concept of ‘quantum tunneling’.
the lifetime of a particle may be sufficiently short for the uncertainty in its energy to give a realistic probability of the particle having sufficient energy to escape from the potential well
or
(particle can) ‘borrow energy’ for a short period of time (to escape from the potential well)
Explain the production of ‘cosmic air showers’ when cosmic rays enter the atmosphere.
The cosmic ray strikes a nucleus creating secondary particles (usually hadrons such as the pion) which in turn collide with other particles and so on creating a ‘shower’ of particles which are detectable a ground level (such as muons, positrons and neutrinos).
‘Cosmic air showers’ provided the very first evidence for sub nuclear particles and the quark model of matter.
Assuming the relationship
y = A sin ωt
derive expressions for velocity and acceleration for an object undergoing simple harmonic motion.
y = A sin ωt
differentiating this gives
v = Aω cos ωt
differentating this again gives
a = -Aω2 sin ωt
= -ω2y
State what is meant by ‘cosmic rays’.
Cosmic rays are high energy particles entering the atmosphere from space.
They consist mainly of protons, electrons and alpha partciles from the sun, known as the solar wind.
Neils Bohr and Louis de Broglie suggested that electrons can be considered as ‘standing waves’ in orbit around the nucleus of an atom.
Using the circumference of an orbit (2πr) being equal to n de Broglie wavelengths (nλ), derive an expression for the quantised angular momentum of an electron.
2πr = nλ
2πr = nh/p (since λ = h/p)
2πr = nh/mv (since p = mv)
mvr = nh/2π
A stationary wave is formed in a piece of elastic string under tension, created by a vibration generator set to 250Hz as shown below.
The distance between adjacent nodes is 0.15m
- Determine the wavelength of this wave.
- Determine the speed of this wave.

- The wavelength of the wave is 0.3m (The distance between nodes is equal to half a wavelength).
- The speed of the wave = frequency x wavelength
= 250 x 0.3
= 75 ms-1
The magnitude of the force on a charged particle entering a magnetic field can be determined using the relationship
F = qvB
where v is the particle’s velocity perpendicular to the magnetic field, B.
How should you deal with particles that do not enter fields perpendicularly?
You should calculate the component of the particle’s velocity perpendicular to the field.
In this example, v would become vsinθ

What is the relationship between the energy transferred by a wave and the amplitude of the wave?
The energy transferred by a wave is proportional to the ampltude squared of the wave.
E = kA2
or
E1A12 = E2A22
Starting with the relationships
y = A sin ωt and v = Aω cos ωt
show that the velocity of a particle undergoing simple harmonic motion can be expressed as
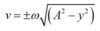
- y = A sin ωt and v = Aω cos ωt
rearranging gives
- sin ωt = y/A and cos ωt = v/Aω
since sin2ωt + cos2ωt = 1
- y2/A2 + v2/A2ω2 = 1
multiplying through by A2ω2
- y2ω2 + v2 = A2ω2
now rearrange for v2
- v2 = A2ω2 - y2ω2
take ω2 out as a common factor
- v2 = ω2(A2 - y2)
square root both sides
- v = ±ω√(A2 - y2)
Considering the circular motion of a charged particle in a magnetic field, derive an expression for the radius of the particle’s circular motion.
The force exerted by the magnetic field is considered to be a centripetal force, and so:
qvB = mv2/r
rearranging this obtains
r = mv/qB
In the early 1900’s, experimental evidence suggested that certain phenomena could not be explained using classical physics theory.
State one experimental observation that cannot be explained by classical physics.
- Bohr model of the atom and energy levels for electrons.
- Emission and absorption spectra produced by elements in gaseous form.
- The photoelectric effect
- Black body radiation curves/ultraviolet catastrophe
Describe the effects of damping in simple harmonic motion. Consider:
- Underdamping
- Overdamping
- Critical damping
- The effects of underdamping are quite small and result in a slow reduction in amplitude.
- The damping is so great that no complete oscillations are seen. (sometimes called heavy damping)
- This means that the oscillator comes to rest in the minimum possible time

There exists some well known experimental evidence for wave-particle duality.
Can you name some experimental evidence which shows the
- Particle nature of waves
- Wave nature of particles.
- The photoelectric effect
- Electron diffraction patterns.
Assuming the relationship
y = A cos ωt
derive expressions for velocity and acceleration for an object undergoing simple harmonic motion.
y = A cos ωt
differentiating this gives
v = -Aω sin ωt
differentating this again gives
a = -Aω2 cos ωt
= -ω2y
Describe how aurorae are produced in the earth’s upper atmosphere
Cosmic rays enter the earth’s magnetic field and spiral with helical motion along the field lines until they enter the earth’s atmosphere at the north and south poles.
Collisions with atoms in the earth’s atmosphere produce energy in the form of light, known as aurora. (Borealis, Northern lights. Australis, Southern lights)
Shown below is an example of a ‘black body radiation curve’ which shows the irradiance of all wavelengths of radiation emitted by an object.
What is the relationship between the ‘peak wavelength’ emitted by an object and its temperature in kelvin?

The shorter the ‘peak wavelength’ of the object, the higher the temperature of the object.
Quantatively, this relationship is known as ‘Wein’s law’ and is given by the relationship
T x λp = 2.9 x 10-3














