Quant Mixed Practice (Can Try Without Paper)

Question 1

What is the formula for counting the number of possible Pairs, from a group of N people/teams/etc? (We could be counting # of handshakes, games between teams, etc)

Answer 1

Question 2

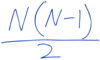
What do we know about the median and average of an evenly spaced set?

What is the formula for the sum of an evenly spaced set?

Answer 2

Median and Average are the same!

Sum = Number of values * Average Value

= N * (First + Last) / 2

Question 3

What is the formula for the number of multiples of a number in a certain range?

If 10 < x < 100, for how many values of x is x/3 an integer?

Answer 3

(Last - First) / Increment + 1

x/3 is an integer is another way of saying “multiples of 3”

(Last - First) / Increment + 1

First is 12. Last is 99. Increment is 3.

(99 - 12) / 3 + 1 = 87/3 + 1 = 30

Question 4

What is the average of x and y?

(1) The average of 2x and y is 8
(2) The average of x and 3y is 10

Answer 4

C- Together

Combo Question: If we know (x + y), it’s sufficient.

We have 2 unique equations, so we can solve for both variables.

DON’T ACTUALLY CALCULATE!

Question 5

What is the average of x and y?

(1) The average of 4x and 4y is 8
(2) The average of x and 3y is 10

Answer 5

A- (1) Alone

Combo Question: If we know (x + y), it’s sufficient.

If one equation is a multiple of the combo, (or can be manipulated to isolate the combo), it’s sufficient:

(1): (4x + 4y) / 2 = 8

2x + 2y = 4

Divide by 2: x + y = 2

We don’t need to write out the equations above, if we are looking for a multiple of the combo and notice it.

Question 6

What is the average of x and y?

(1) The average of 2x and 6y is 20
(2) The average of x and 3y is 10

Answer 6

E - Not Sufficient

Combo Question: If we know (x + y), it’s sufficient.

If we have 2 unique equations, we can solve for both variables.

But we need to check that equations are unique. Also check that they’re not a multiple of the combo.

(1) (2x + 6y) / 2 = 20

Divide by 2 on both sides:

(x+3y) / 2 = 10 –> (1) and (2) are the same equation, not unique!

Question 7

What is 2x - 3y ?

(1) 4x - 6y = 8
(2) -9y + 6x = 12

Answer 7

D- Each Statement Alone

Check if the statements can be manipulated to isolate the combo “2x - 3y”:

(1) 4x - 6y = 8

Divide by 2: 2x - 3y = 4 –> Sufficient

(2) -9y + 6x = 12

Divide by 3: -3y + 2x = 4

Order of addition is reversed, this is same as 2x - 3y = 4 –> Sufficient

Question 8

At a fish market, 1/4 are cod and 1/6 are salmon. How many of the fish are cod?

(1) There are 108 salmon.
(2) There are 3 cod for every 2 salmon.

Answer 8

A –> (1) Alone

F = Total Fish

Rephrase: C = 1/4 F, S = 1/6 F, C =?

We have 2 unique equations, 3 variables. With 1 more unique equation we can solve.

(1) S = 108 –> Sufficient DON’T CALCULATE!
(2) Insufficent. Trap–> not unique, same info as prompt! We already have the ratio of cod to salmon:

(1/4) / (1/6) = (3/12) / (2/12) = 3/2

Question 9

What is the most important way to reduce careless errors?

Answer 9

READING– Double check what it’s asking for!

Examples:

“Increasing” vs “Decreasing” order

“Shaded” vs “Unshaded” area

Solving for X, but question asks for Y

Before you hit “Confirm”, that can be a good cue to check that you answered the right question.

Also, read the constraints carefully!

Example: “If x is a POSITIVE integer,…”

Question 10

Answer 10

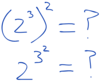
1) Multiply the powers
2) Order of operations requires doing the 3² first.

Question 11

xy < xz

Is y < z?

Answer 11

Yes, if x is positive.

No, if x is negative.

Remember, with inequalities, we flip the sign if we multiply or divide by a negative number.

Question 12

Is the average of the following greater than 50?

40, 45, 45, 50, 50, 52, 57, 58

For speed, use the over/under method– find the total difference less than 50, and compare to the total difference greater than 50.

Answer 12

Under: 40, 45, 45 –> 10 + 5 + 5 = 20 under

Over: 52, 57, 58 –> 2 + 7 + 8 = 17 over

More under than over –> NO, average is less than 50.

Question 13

What is the formula for finding the midpoint of a line between 2 points?

Answer 13

(Average of the x values, Average of the y values)

Question 14

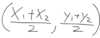
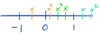
For what values of x is x² < x ?

Answer 14

Drawing / Visualizing the number line can be helpful!

If x is negative, x² is positive, so x² is greater.

If x is > 1, x² is greater

If 0 < x < 1, x² is LESS than x

Question 15

For what values of x is x³ < x²

Answer 15

If x < 1, x³ is less than x²

If x is negative, x³ is negative & x² is positive

If x is between 0 and 1, x³ will be less than x², because multiplying by x each time makes it smaller

Question 16

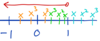
For what values of x is x³ > x ?

Answer 16

-1 < x < 0 , x > 1

Between -1 and 0, and greater than 1

Question 17

8 machines can complete a job in 6 days. How many additional machines are needed to complete the job in 4 days?

Answer 17

Fastest way: to do something in 2/3 the time, we need 3/2 the number of machines to compensate. (W = NRT)

8 * 3/2 = 12 –> 12 - 8 = 4

Equations way: First, find Rate for 1 machine:

W = NRT –> R (for 1 machine) = W / (NT)

R = 1 / (8*6) = 1/48

Then solve for N:

W = NRT–> N * 1/48 * 4 = 1 –> N = 12

Then be sure to answer the question asked –> “Additional Machines”

12 - 8 = 4

Question 18

If n is a positive integer and the product of all the integers from 1 to n, inclusive, is a multiple of 1300, what is the least possible value of n?

What can we conclude from “multiple of 1300”?

What does “product of all the integers from 1 to n translate to?”

Answer 18

13

“A multiple of 1300” translates to “1300 is a factor”

Find the prime factors of 1300:

1300 = 13 * 10 * 10 = 2^2 * 5^2 * 13

“The product of all integers from 1 to n” translates to n! (n factorial)

10! gives us 2 factors of 5, and 8 factors of 2, but we still need a factor of 13

13! is the lowest factorial that includes 13.

Question 19

What is the 1st step for this problem?

DS: If it took 15 minutes to run home, was the distance less than 3 miles?

(1 mile = 5,280 feet)

(1) The average speed was less than 19 feet per second
(2) The average speed was greater than 17 feet per second

Answer 19

Both statements are in ft/second –> so convert prompt to ft/second

Question 20

If d is the standard deviation of x, y, and z,

A) what is the standard deviation of x + 2, y + 2, z +2?

B) What is the standard deviation of 4x, 4y, 4z?

Answer 20

A) d. The standard deviation is how spread out the data is. Adding to each data point doesn’t change it.

B) 4d. The data will be 4 times as spread out.

Question 21

If diameter AB = 13 and BC = 5, what is the area of triangle ABC?

Answer 21

A triangle inscribed inside a semicircle is a Right Triangle.

5-12-13 is a Pythagorean Triple, or you can calculate:

a^2 + b^2 = c^2 –> a^2 = c^2 - b^2

13^2 - 5^2 = 144 = (AC)^2 –> AC = 12

Area = base * height / 2 (with base and height perpendicular)

Area = 12*5/2 = 30

Question 22

Are less than 10 percent of the people in country Y who are 30 years old unemployed?

(1) In Country Y, of the population who are 30 years old, 10 percent of women is unemployed, and 13 percent of men is unemployed
(2) In country Y, 11 percent of the population is unemployed

Answer 22

A – (1) Alone

(1) Depending on the ratio of men to women, the percent of the people who are 30 who are unemployed can range between 10% to 13%. The answer is “No”, it can’t be “less than 10 percent”
(2) We care specifically about people who are 30, not the population as a whole. This doesn’t help –> Insufficent.

Question 23

What is the equation for a circle on a graph?

How would we repesent (x, y) lies inside the circle?

Answer 23

x² + y² = r²

This is based off of the Pythagorean Theorem.

(x, y) lies inside the circle: x² + y² 2

Question 24

In a pet shop, 20 percent of the pets are dogs. 1/4 are cats. How many dogs are there?

(1) There are 22 pets that are neither dogs nor cats.
(2) There are 2 fewer dogs than cats

Answer 24

D –> Each statement alone

T = Total pets, D = Dogs, C = Cats

D = 1/5 T, C = 1/4 T

If we can find T, it’s sufficient. We need 1 more unique equation.

(1) 22 = the number that aren’t cats or dogs –> Clearly a unique equation

Don’t need to write out, but equation is: (22 = T - 1/5T - 1/4T = T - 4/20T - 5/20T = 11/20T –> T=40

(2) Also a unique equation: D = C - 2

Question 25

What is true about the sides of a parallelogram?

The angles?

The right triangles created by the yellow lines?

Answer 25

Opposite sides are =

Opposite angles are =

All 4 right triangles are =

Question 26

If below is the graph of y = (x+1)², what would the graph of y = (x+1)² - 1 look like?

Answer 26

It would shift 1 unit DOWN.

The y-value is being reduced by 1.

Question 27

If 0 < x < 4, what is the median of the numbers x, 1, 3, 5, 6?

(1) 13x - 39 = 13
(2) (x-4)(x-5) = 0

Answer 27

D: Each Alone

Median is the middle number, so:

If x < 3, median is 3

If 3 < x < 5 , median is x

If 5 < x , median is 5

(1) Linear equation –> can solve for 1 value of x –> Sufficient –> Don’t Calculate!
(2) x = 4 OR x = 5. Trap: looks Insufficent, but prompt says 0 < x < 4, so only 1 value for x –> Sufficient

Question 28

If the ratio of the black shaded area to the unshaded area of the triangle is 1 to 3, what is the unshaded area?

Answer 28

Total area of triangle = 8 * 4 / 2 = 16

1:3 ratio means 3/4 of the total is unshaded

3/4 * 16 = 12

Question 29

How do we tell if a fraction is a “terminating decimal”?

Answer 29

AFTER the fraction is simplified, the prime factorization of the denominator includes only 2’s and 5’s.

Question 30

Which of the following fractions has a decimal equivalent that is a terminating decimal?

A. 7/42
B. 9/33
C. 3/600
D. 25/144
E. 24/210

Answer 30

C: 3/600

Terminating Decimal –> After the fraction is simplified, the prime factorization of the denominator includes only 2’s and 5’s.

A: 1/6 –> Has a 3 in denominator

B: 3/11 –> Has 11 in denominator

C: Simplifies to 1/200. 200 quickly factors into 100 * 2 = 2^2 * 5^2 * 2 –> only 2’s and 5 –> Terminating

D: 144 factors to 3² * 2⁴. 25 = 5*5. We still have 2 3’s on denominator.

E: 210 = 3*7*10. 24 = 3 * 8, so the 3 crosses off, but we still have a 7 in the denominator.

Question 31

If A and B are positive integers and R is the remainder when 2(10^A) + B is divided by 3, what is the value of R?

1) a=10
2) b=1

Answer 31

The remainder will be 0 if the number is a multiple of 3.

(R = 1 if 1 more than multiple of 3, and R = 2 if 2 more than multiple of 3)

How do we test for divisibility by 3?

If the sum of the digits is a multiple of 3, it’s divisible by 3.

1) Insufficient. We don’t know b. If B = 1, R = 0. If B = 2, R = 1, if B = 3, R = 2.
(2) Sufficient. Since A is a positive integer, the power of A doesn’t affect the sum of the digits, and therefore the divisibility. It just adds more zeros to the number.

Clearly they are sufficient together, but this is a “C Trap”. We don’t need (1)!