Q2: Fractions, Decimals, Percents

Question 1

Answer 1

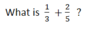
For adding & subtracting fractions, first find a common denominator (Least Common Multiple of 3 and 5)

Question 2

Answer 2

Question 3

Answer 3

Question 4

Answer 4

Question 5

Answer 5

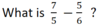
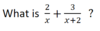
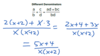
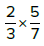
Multiply horizontally:

Question 6

Answer 6

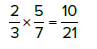
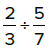
Dividing fractions: Flip the 2nd fraction and multiply

Question 7

Answer 7

Question 8

Answer 8

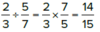
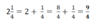
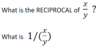
When we take the RECIPROCAL, we flip the fraction

This is the same as 1 divided by the fraction.

Question 9

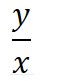
Write “z is x percent of y” as an equation

Answer 9

Percent means “divide by 100”

“of” means “multiply”

“is” means =

Question 10

Write “x is 20% greater than y” as an equation

Answer 10

Question 11

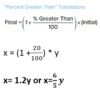
Write “x is 15% less than y” as an equation,

a) write using a decimal
b) convert to a fraction

Answer 11

Question 12

Write “x is n percent greater than y” as an equation

Answer 12

Question 13

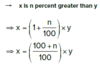
A bike was $50, and is now on sale for $32. What is the percent change in price?

Answer 13

Question 14

Distribute:

-3(x-7)

Answer 14

= -3*x + -3*-7

= -3x + 27

Be careful with your SIGNS! Double negative turns into a positive

Question 15

Factor out the Common Factor:

4x + 4y =7

Answer 15

Both terms have “4” as a factor.

So, we can factor it out (this is the inverse process to “distribution”)

4(x+y) = 7

Question 16

Factor out the Common Factor:

3x + 6y + 15z = 7

Answer 16

Factor out the Common Factor:

The common factor between 3, 6, and 15 is 3.

(we can prove this by writing the prime factorization: 6=2*3, 15=5*3)

We factor out 3 from each “term”.

3(x + 2y + 5z)

Question 17

Multiplying Exponents:

What is 2³ * 2⁴ ?

Answer 17

2⁷

When we multiply exponents with the same bases, we add the powers

a^b * a^c = a^b+c

Question 18

What is 2 * x³ * y² * 3 * y⁴ * x ?

Answer 18

We match up what can be simplified:

2*3 = 6

x³ * x = x⁴

y² * y⁴ = y⁶

6x⁴y⁶

Question 19

Distribute: -2x(-3x + 5)

Answer 19

• 2x * -3x = 6x²
• 2x * 5 = -10x

6x² - 10x

Question 20

Factor out the Common Factor:

15x² - 10x

Answer 20

This time, we can factor out both a number and a variable:

The common prime factor of 15 and 10 is 5.

The common variable is x

So, we factor out 5x:

5x(3x-2)

Question 21

Scientific Notation:

Write out as a number: 2.3 * 10⁷ = ?

Answer 21

23,000,000

* 10⁷ is like multiplying by 10, 7 times. This moves the decimal point 7 places to the right.

Question 22

What is the units digit, tens digit, and hundreds digit of the number 5318?

Answer 22

units: 8
tens: 1
hundreds: 3

Question 23

What is the units digit of 32¹⁹ ?

Answer 23

We need to find the pattern.

32¹⁹ will have the same units digit as 2¹⁹

2¹ = 2

2² = 4

2³ = 8

2⁴ = 16

2⁵ = 32

2⁶ = 64

The pattern repeats for every 4 numbers in the pattern: {2, 4, 8, 6}

Every 4th power will have a units digit of 6: 2⁴, 2⁸, 2¹², 2¹⁶

So, 2¹⁷ ends in 2, 2¹⁸ ends in 4, 2¹⁹ ends in 8.

Question 24

What is units digit of 7¹⁴

Answer 24

7¹ =7

7² = 49

Only the units digit will affect the next power: so we can do 9*7 =63 –> 7³ ends with 3

3*7 =21 –> 7⁴ ends with 1

1*7 = 7 –>7⁵ ends with 7.

So, the pattern repeats for every 4 numbers in the pattern: {7, 9, 3, 1}

So, the 4th, 8th, and 12th powers would have units digit of 1.

7¹³ has units digit of 7

7¹⁴ has units digit of 9

Question 25

If x and y are integers, with y > 1, how do we determine whether the fraction x/y is a repeating decimal (for example, 1/3 = .33333333… repeating), versus a “Terminating Decimal” with a finite number of digits (example: 1/40 = 0.025)?

Answer 25

The numerator doesn’t matter.

If the denominator only includes the prime factors 2 and/or 5, it is not repeating.

Example: 1/200 = ?

200 = 2*2*2*5*5 —> so it will be a “Terminating Decimal”

1/200 = 0.005

1/60= 3*2*2*5 = .01666666…… —> “Repeating Decimal”