Puzzles

Question 1

Hans is standing behind Gerrie and at the same time Gerrie
is standing behind Hans. How is this possible?

Answer 1

Hans and Gerrie are standing with their backs towards each other!

Question 2

In Miss Miranda’s class are eleven children. Miss Miranda has a bowl with eleven apples. Miss Miranda wants to divide the eleven apples among the children of her class, in such a way that each child in the end has an apple, but one apple still remains in the bowl. Can you help Miss Miranda?

Answer 2

Ten children get a single apple, and the eleventh gets the bowl with an apple still in it.

Question 3

It is greater than GOD, the poor have it, the rich want it, but if you eat it you will die. What is it?

Answer 3

Nothing!

Question 4

You have five pieces of chain, each consisting of three links.You want to make one long chain of these five pieces. Breaking open a link costs 5 rupees, and welding an open linkcosts 15 rupees. Is it possible to make one long chain of the five pieces, if you have just 70 rupees?

Answer 4

First, break open all three links of one of the pieces of chain. This costs 3×5 = 15 rupees. Then join the remaining four pieces of chain with the three open links. Welding these links costs 3×15 = 45 rupees. The total cost is 60 rupees.

Question 5

Julius and Vincent are brothers. “We are born within the same hour,” says Julius, “on the same day of the same year.” “But,” says Vincent, “we are no twins!”. How is this possible?

Answer 5

Julius and Vincent are part of a set of triplets, or quadruplets, or even more.

Question 6

Using the digits 1 up to 9, three numbers (of three digits each) can be formed, such that the second number is twice the first number, and the third number is three times the first number. Which are these three numbers?

Answer 6

There are four solutions:

192, 384, and 576.
219, 438, and 657.
273, 546, and 819.
327, 654, and 981.

Question 7

Joyce has bought ten trees for her garden. She wants to plant these trees in five rows, with four trees in each row. How should she plant them?

Joyce’s neighbour George has bought nine trees for his garden. How can he plant these nine trees in ten rows, with three trees in each row?

Answer 7

Question 8

Here you see a fish swimming to the left.

Can you make it swim to the right by moving just three sticks?

Answer 8

Question 9

Here you see a triangle formed by ten coins. The triangle points upwards. How can just three coins be moved to make the triangle point downwards?

Answer 9

Question 10

Peasant Janet kept six pigs in six pens of equal size, made with thirteen wooden fences (see the picture on the right). One night, there was a terrible storm, in which one of the thirteen fences was badly damaged. Janet rearranged the remaining fences so that the six pigs still each had pens of equal size. How did she do it?

Answer 10

Question 11

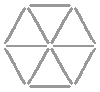
Can you draw this house in one stroke (i.e., without lifting the pen from the paper) and without crossing an already drawn part?

Answer 11

Question 12

Take a coin from your wallet (a 1 or 2 Euro piece works best).Take a piece of paper and cut a circular hole in it middle, which is slightly smaller than the size of the coin (a diameter which is roughly 80% of the diameter of the coin, see picture). How can you get the coin through the hole without breaking or cutting the paper?

Answer 12

Fold the paper in two across the hole. Place the coin inbetween the two halves, already partly slipping through the hole. Then pull at both ends of the folded paper to enlarge the hole and the coin will fall through: see picture.

Question 13

Twelve sticks form four equal squares. How can exactly three sticks be moved to make three equal squares?

Answer 13

Question 14

Twelve sticks form four equal squares. How can exactly four sticks be moved to make three equal squares?

Answer 14

Question 15

By moving only two sticks, these three equal sized squares can be changed into four equal sized rectangles. How?

Answer 15

Four small, equal sized rectangles:

Question 16

On the right you see six sticks Can you rearrange these six sticks to leave nothing?

Answer 16

Question 17

In a contest, four fruits (an apple, a banana, an orange, and a pear) have been placed in four closed boxes (one fruit per box). People may guess which fruit is in which box. 123 people participate in the contest. When the boxes are opened, it turns out that 43 people have guessed none of the fruits correctly, 39 people have guessed one fruit correctly, and 31 people have guessed two fruits correctly. How many people have guessed three fruits correctly, and how many people have guessed four fruits correctly?

Answer 17

If three guesses were correct, then so is the fourth! So all the remaining 10 people guessed all the four fruits correctly.

Question 18

A long, long time ago, two Egyptian camel drivers were fighting for the hand of the daughter of the sheik of Abbudzjabbu. The sheik, who liked neither of these men to become the future husband of his daughter, came up with a clever plan: a race would determine who of the two men would be allowed to marry his daughter. And so the sheik organized a camel race. Both camel drivers had to travel from Cairo to Abbudzjabbu, and the one whose camel would arrive last in Abbudzjabbu, would be allowed to marry the sheik’s daughter.The two camel drivers, realizing that this could become a rather lengthy expedition, finally decided to consult the Wise Man of their village. Arrived there, they explained him the situation, upon which the Wise Man raised his cane and spoke four wise words. Relieved, the two camel drivers left his tent: they were ready for the contest! Which 4 wise words did the Wise Man speak?

Answer 18

“Take each other’s camel.”

Question 19

A boy leaves home in the morning to go to school. At the moment he leaves the house he looks at the clock in the mirror. The clock has no number indication and for this reason the boy makes a mistake in interpreting the time (mirror-image). Just assuming the clock must be out of order, the boy cycles to school, where he arrives after twenty minutes. At that moment the clock at school shows a time that is two and a half hours later than the time that the boy saw on the clock at home.

At what time did he reach school?

Answer 19

The difference between the real time and the time of the mirror image is two hours and ten minutes (two and a half hours, minus the twenty minutes of cycling). Therefore, the original time on the clock at home that morning could only have been five minutes past seven:

The difference between these clocks is exactly 2 hours and ten minutes (note that also five minutes past one can be mirrored in a similar way, but this is not in the morning!).Conclusion: The boy reaches school at five minutes past seven plus twenty minutes of cycling, which is twenty-five minutes past seven!.

Question 20

A piece of paper of size 5 by 5 with two blunted corners should be divided into no more than two pieces (i.e. just one cut in total) and be rearranged into size 6 by 4 as shown in the figure below. How should the the paper be cut?

Answer 20

Question 21

Answer 21

Question 22

In front of you are 10 bags, filled with marbles. The number of marbles in each bag differs, but all bags contain ten marbles or more. Nine of the ten bags only contain marbles of 10 grams each. One bag only contains marbles of 9 grams. In addition, you have a balance which can weigh in grams accurate, and you are allowed to use it only once (i.e. weigh a single time).

How can you find out in one weighing, which bag contains the marbles of 9 grams?

Answer 22

Number the ten bags from 1 up to and including 10. Then take one marble from bag 1, two marbles from bag 2, three marbles from bag 3, etc. Place all 55 marbles that you selected from the bags together on the balance. The number of grams that the total weight of these 55 marbles differs from 550 grams, is equal to the number of marbles of 9 grams that are among those 55 marbles, and that is equal to the number of the bag which contains the marbles of 9 grams!

Question 23

William lives in a street with house-numbers 8 up to 100. Lisa wants to know at which number William lives. She asks him: “Is your number larger than 50?”William answers, but lies. Upon this, Lisa asks: “Is your number a multiple of 4?” William answers, but lies again.Then Lisa asks: “Is your number a square?” William answers truthfully. Upon this, Lisa says: “I know your number if you tell me whether the first digit is a 3.” William answers, but now we don’t know whether he lies or speaks the truth. Thereupon, Lisa says at which number she thinks William lives, but (of course) she is wrong.

What is Williams real house-number?

Answer 23

Note that Lisa does not know that William sometimes lies. Lisa reasons as if William speaks the truth. Because Lisa says after her third question, that she knows his number if he tells her whether the first digit is a 3, we can conclude that after her first three questions, Lisa still needs to choose between two numbers, one of which starts with a 3. A number that starts with a 3 must, in this case, be smaller than 50, so William’s (lied) answer to Lisa’s first question was “No”. So, In reality, William’s number is larger than 50, not a multiple of 4, and a square. Of the squares larger than 50 and at most 100 (these are 64, 81, and 100), this only holds for 81.

Question 24

Three blondes are celebrating their success in a pub.The bartender asks them: “Girls, what’s the reason for the celebration?

Answer 24

One of the blondes responds: “Well, we just finished this puzzle and it took us only a month, while the box indicated: 3 to 6 years!”…

Question 25

You are riding a horse. In front of you there is a fire engine. You are being followed by a helicopter. To your left a sports car is driving. And to your right there is a depth.

How can you arrange that you will all stop simulaneously, without crashing and without mutual communication?

Answer 25

You ask the man of the merry-go-round to stop it.

Question 26

What does this picture represent?

Answer 26

A giraf that walks past a window.

Question 27

What can you put in a barrel which makes it lighter?

Answer 27

A hole.

Question 28

If you had only one match and entered a cold and dark room, where there were a fire place, an oil lamp and a candle, which would you light first?

Answer 28

The match!

Question 29

You take a bite from your apple and find a worm in the apple. What is even worse?

Answer 29

Taking a bite from your apple and finding only half a worm in the apple!

Question 30

A man is standing in front of a painting of a man, and he tells us the following: “Brothers and sisters have I none, but this man’s father is my fathers son”. Who’s on the painting?

His father
He himself
His son

Answer 30

His son.

Question 31

Imagine you are on an island called Texel, with inhabitants that look the same from the outside, but differ from inside (their truthfulness). We distinguish the following types:

Knights, who always tell the truth.
Knaves, who never tell the truth.
Normals, who sometimes tell the truth and sometimes lie.
Assume you meet one of these inhabitants, and he tells you: “I’m no Knight”. Then, of what type is inhabitant?

Knight
Knave
Normal
Indeterminable

Answer 31

The Solution: Normal

A Knight cannot make the statement “I’m no Knight”, since this would be a lie and a Knight always tells the truth. A Knave could also not make the statement, since that would be a true statement, and a Knave never tells the truth. A Normal however can say “I’m no Knight”. It’s true, and Normals sometimes tell the truth.

Question 32

A hunter leaves his cabin early in the morning and walks one mile due south. Here he sees a bear and starts chasing it for one mile due east before he is able to shoot the bear. After shooting the bear, he drags it one mile due north back to his cabin where he started that morning. What color is the bear?

Black
Brown
White
Gray

Answer 32

White.

Question 33

Recall the island Texel with its inhabitants: Knights (who always tell the truth), Knaves (who always lie) and Normals (who sometimes lie and sometimes tell the truth). On this island, a man and a woman may only marry in case they are both Normal, or one of them is a Knight and the other one is a Knave. Now you meet Mr. and Mrs. A who tell you the following:Mr. A: “My wife is not normal” Mrs. A: “My husband is not normal”

What types of persons are Mr. and Mrs. A?

They are both Normal.
Mr. A is a Knight and Mrs. A is a Knave.
Mr. A is a Knave and Mrs. A is a Knight.
Indeterminable

Answer 33

The Solution: They are both Normal.

As stated in the question, the man and a woman may only marry in case they are both Normal, or one of them is a Knight and the other one is a Knave. So, there are only three possibilities: they are both Normal, or Mr. A is a Knight and Mrs. A is a Knave, or Mr. A is a Knave and Mrs. A is a Knight. Assume Mr. A is a Knight and Mrs. A is a Knave. Then both tell the truth, which is impossible since Mrs. A should always lie. Assume Mr. A is a Knave and Mrs. A is a Knight. Then again both tell the truth, which is impossible since now Mr. A should always lie. The only remaining possibility is that both Mr. A and Mrs. A are Normal.

Question 34

The birthday cake on the picture must be cut into eight equally sized pieces. However, you are allowed to make only 3 straight cuts.

Answer 34

There is only one solution which solves the problem with three straight cuts, and leaves exactly eight equally shaped portions. One should cut the cake two times vertically in a ‘+’ shape across the top and make the third cut horizontally in the middle of the cake (looking at the cake from the front), as shown in the figure on the right. The disadvantage of this solution is however that only four portions will contain fruit-decoration etc., whereas the other four portions will only contain bottom parts of the cake…

Question 35

Two whole numbers, m and n, have been chosen. Both are unequal to 1 and the sum of them is less than 100. The product, m × n, is given to mathematician X. The sum, m + n, is given to mathematician Y. Then both mathematicians have the following conversation:
X: “I have no idea what your sum is, Y.”
Y: “That’s no news to me, X. I already knew you didn’t know that.”
X: “Ahah! Now I know what your sum must be, Y!”
Y: “And now I also know what your product is, X!”

What are the numbers m and n?

Answer 35

Let a be equal to m × n and let b be equal to m + n.

From the first remark (X: “I have no idea what your sum is, Y.”) follows that a can be factorized in more than one way. If, for example, X would have got the number 21, which is the product of the prime numbers 3 and 7, then he would have known immediately that Y could only have got 3+7=10 as sum.

From the second remark (Y: “That’s no news to me, X. I already knew you didn’t know that.”) follows that b cannot be written as the sum of two prime numbers. This also implies that b is not even, because each even number can be written as the sum of two prime numbers. If, for example, Y would have got the number 10, which is equal to 2+8, 3+7, 4+6, or 5+5, then Y could not have known for sure that X could not find out his sum, because X might have got the number 3×7=21 and immediately have known Y’s number.

…… more such … the numbers are 4 and 13.

Question 36

In a small village in the middle of nowhere, three innocent prisoners are sitting in a jail. One day, the cruel jailer takes them out and places them in a line on three chairs, in such a way that man C can see both man A and man B, man B can see only man A, and man A can see none of the other men. The jailer shows them 5 hats, 2 of which are black and 3 of which are white. After this, he blindfolds the men, places one hat on each of their heads, and removes the blindfolds again. The jailer tells his three prisoners that if one of them is able to determine the color of his hat within one minute, all of them are released. Otherwise, they will all be executed. None of the prisoners can see his own hat, and all are intelligent. After 59 seconds, man A shouts out the (correct) color of his hat!

The Question: What is the color of man A’s hat, and how does he know?

Answer 36

The answer: man A is wearing a white hat.

An explanation:
From the fact that neither B nor C gives an answer, we conclude that both these men have insufficient information to determine the color of their hats. Let us start with man C. He must be seeing at least one white hat on the heads of A and B (if he would see two black hats, he would know that he is wearing a white hat). Man B therefore knows that he and/or A is wearing a white hat. Since he cannot give an answer, he must be seeing a white hat on A’s head (if B would see A wearing a black hat, he would know that he himself wears a white one). From the fact that neither C nor B can give an answer to the jailer’s question, A finally concludes that he is wearing a white hat!

Question 37

You have a stack of 23 cards. Each card has an image of a cross on one side, and an image of a circle on the other side. You know that 14 cards in the stack are laying with the cross up, and therefore 9 cards are with the circle up. But you don’t know in which order the cards are. Moreover, you are in a completely dark room, so you can’t see anything.

How can you, without seeing anything, divide the stack of cards in two smaller stacks, in such a way that both stacks have the same number of cards with a cross up?

Answer 37

Take 14 cards from the stack. Of these 14 cards, k cards are with the cross up, and therefore 14-k cards are with the circle up. In the remaining stack of 9 cards are 14-k cards with a cross up.

Then turn the stack of 14 cards round. Now there are 14-k cards with a cross up in both stacks.

Note that we do not know exactly how many cards are laying with a cross up in both stacks (or how many cards are laying with a circle up). We only know that both stacks have the same number of cards with a cross up.

Question 38

Archimedes discovered the first law of hydrostatics: when a body is immersed in a fluid, it experiences an upward buoyant force which is equal to the weight of the fluid displaced by the immersed part of the body.

“Eureka!”

In an aquarium filled with water, a block of ice floats. We mark the current water level. When the ice has molten completely, will the water level be higher, lower, or still the same?

Answer 38

Solution to: Eureka!
The upward force, needed to keep a block of ice floating, is equal to the weight of the ice. According to Archimedes, the weight of the ice therefore equals the weight of the displaced water. But when the ice has melted, the weight of the resulting water still equals the original weight of the ice. So the amount of water from the melted ice equals the amount of displaced water.

Conclusion: the water level stays the same.

Question 39

Molly has a set of four alphabet blocks. Each side of these blocks is printed with a different letter, making 24 in total. Molly notices that by rearranging the blocks, she can spell each of the following words:

BOXY, BUCK, CHAW, DIGS, EXAM, FLIT,
GIRL, JUMP, OGRE, OKAY, PAWN, ZEST

Which letters are on each block?

Answer 39

From the word EXAM, we conclude that E and A are not on the same block.
From the word OGRE, we conclude that E and O are not on the same block.
From the word OKAY, we conclude that A and O are not on the same block.
Combining these, we conclude that A, E, and O are on different blocks. Assume that A is on block 1, E is on block 2, and O is on block 3.

From the words BOXY and EXAM, we conclude that X is not on the same block as A (block 1), E (block 2), and O (block 3), so X is on block 4.
From the words BOXY and OKAY, we conclude that Y is not on the same block as A (block 1), O (block 3), and X (block 4), so Y is on block 2.
From the word EXAM, we conclude that M is not on the same block as A (block 1), E (block 2), and X (block 4), so M is on block 3.
From the word OKAY, we conclude that K is not on the same block as A (block 1), Y (block 2), and O (block 3), so K is on block 4.
From the word BOXY, we conclude that B is not on the same block as Y (block 2), O (block 3), and X (block 4), so B is on block 1.
From the words BUCK and JUMP, we conclude that U is not on the same block as B (block 1), M (block 3), and K (block 4), so U is on block 2.
From the words PAWN and JUMP, we conclude that P is not on the same block as A (block 1), U (block 2), and M (block 3), so P is on block 4.
From the word JUMP, we conclude that J is not on the same block as U (block 2), M (block 3), and P (block 4), so J is on block 1.
From the words CHAW and BUCK, we conclude that C is not on the same block as A (block 1), U (block 2), and K (block 4), so C is on block 3.
From the words CHAW and PAWN, we conclude that W is not on the same block as A (block 1), C (block 3), and P (block 4), so W is on block 2.
From the word CHAW, we conclude that H is not on the same block as A (block 1), W (block 2), and C (block 3), so H is on block 4.
From the word PAWN, we conclude that N is not on the same block as A (block 1), W (block 2), and P (block 4), so N is on block 3.
Now, we must still have three letters for block 1, and two letters for each of the blocks 2, 3, and 4. We have the following letters left:

D, F, G, I, L, R, S, T, Z
From the words DIGS, FLIT and GIRL, we conclude that I is not on the same block as D, F, G, L, R, S, and T, so I is on the same block as Z. Furthermore, I and Z are on block 2, 3, or 4.
From the word ZEST, we conclude that Z is not on the same block as E (block 2), so Z is on block 3 or 4.
From the word OGRE, we conclude that G and R are not on the same block as E (block 2), and O (block 3), so G and R are on block 1 or 4, but not on the same block.
From the word GIRL, we conclude that I is not on the same block as G and R (block 1 or 4), so I is on block 2 or 3. Since Z is on block 3 or 4, I and Z must be on block 3. Now we have all six letters of block 3: C, I, M, N, O, and Z.
From the word GIRL, we conclude that L is not on the same block as G and R (block 1 and 4), so L is on block 2.
From the words FLIT and GIRL, we conclude that F, G, L, R, and T are not on the same block as L (block 2), and from the word ZEST, we conclude that S is not on the same block as E (block 2). So D must be on block 2.
Now we have all six letters of block 2: D, E, L, U, W, and Y.
From the words GIRL and DIGS, we conclude that G is not on the same block as R and S.
From the words FLIT and ZEST, we conclude that T is not on the same block as F and S.
Combining this, F, R, and S must be on the same block (block 1), and G and T must be on the same block (block 4).
Now we have all six letters of all blocks:
Block 1: A, B, F, J, R, and S.
Block 2: D, E, L, U, W, and Y.
Block 3: C, I, M, N, O, and Z.
Block 4: G, H, K, P, T, and X.

Question 40

You are sitting with one opponent at an empty, round table. Taking turns, you should place one euro on the table, in such a way that it touches none of the coins that are already on the table. The first player that is not able to place a euro on the table, has lost. By tossing a coin it has been decided that you may start.

Which strategy will you follow to make sure you are guaranteed to win?

Answer 40

Put the first euro exactly in the middle of the table. Place each next coin “mirrored” to the coin your opponent has just placed: draw an imaginary line from the last coin of your opponent, through the center of the table, and place your coin on that line, exactly as far from the center of the table as your opponent’s coin. In this way, you are sure that you can always place a euro and that your opponent is the first one that can no longer place a euro.

Question 41

You have a painting with a string attached to it. The string is attached to the upper two corners of the painting. In the wall there are two nails, horizontally next to each other. The string must be hung on the nails in such a way that the painting falls down if any of the two nails is pulled out of the wall. The painting must hang under the nails and must hang on the string.

How must the painting be hung?

Answer 41

One way to do it

Question 42

Jack and his wife went to a party where four other married couples were present. Every person shook hands with everyone he or she was not acquainted with. When the handshaking was over, Jack asked everyone, including his own wife, how many hands they shook. To his surprise, Jack got nine different answers.

How many hands did Jack’s wife shake?

Answer 42

Because, obviously, no person shook hands with himself or herself, or with his or her partner, nobody shook hands with more than eight other people. And since nine people shook hands with different numbers of people, these numbers must be 0, 1, 2, 3, 4, 5, 6, 7, and 8.

The person who shook 8 hands, shook hands with all other persons (who therefore shook each at least 1 hand), except with his or her partner. Therefore, the partner of the person who shook 8 hands, must be the person who shook 0 hands.

The person who shook 7 hands, shook hands with all other persons (who therefore shook each at least 2 hands), except with his or her partner and the person who shook 0 hands. Therefore, the partner of the person who shook 7 hands, must be the person who shook 1 hand.

The person who shook 6 hands, shook hands with all other persons (who therefore shook each at least 3 hands), except with his or her partner and the persons who shook 1 and 0 hands. Therefore, the partner of the person who shook 6 hands, must be the person who shook 2 hands.

The person who shook 5 hands, shook hands with all other persons (who therefore shook each at least 4 hands), except with his or her partner and the persons who shook 2, 1, and 0 hands. Therefore, the partner of the person who shook 5 hands, must be the person who shook 3 hands.

The only person left, is the one who shook 4 hands, and which must be Jack’s wife. The answer is: Jack’s wife shook 4 hands.

Question 43

Tom has three boxes with fruits in his barn: one box with apples, one box with pears, and one box with both apples and pears. The boxes have labels that describe the contents, but none of these labels is on the right box.

How can Tom, by taking only one piece of fruit from one box, determine what each of the boxes contains?

Answer 43

Tom takes a piece of fruit from the box with the labels ‘Apples and Pears’. If it is an apple, then the label ‘Apples’ belong to this box. The box that said ‘Apples’, then of course shouldn’t be labeled ‘Apples and Pears’, because that would mean that the box with ‘Pears’ would have been labeled correctly, and this is contradictory to the fact that none of the labels was correct. On the box with the label ‘Appels’ should be the label ‘Pears’. If Tom would have taken a pear, the reasoning would have been in a similar way.

Question 44

Assume that you have a number of long fuses, of which you only know that they burn for exactly one hour after you lighted them at one end. However, you don’t know whether they burn with constant speed, so the first half of the fuse can be burnt in only ten minutes while the rest takes the other fifty minutes to burn completely. Also assume that you have a lighter.

How can you measure exactly three quarters of an hour with these fuses?

(Hint: You can light several fuses simultaneously; you can also light a fuse a second time after a time interval.)

Answer 44

With only two fuses that burn exactly one hour, one can measure three quarters of an hour accurately, by lighting the first fuse at both ends and the other fuse at one end simultaneously. When the first fuse is burnt out after exactly half an hour (!) you know that the second fuse still has exactly half an hour to go before it will be burnt completely, but we won’t wait for that. We will now also light the other end of the second fuse. This means that the second fuse will now be burnt completely after another quarter of an hour, which adds up to exactly three quarters of an hour since we started lighting the first fuse!

Question 45

A traveler, on his way to Eindhoven, reaches a road junction, where he can turn left or right. He knows that only one of the two roads leads to Eindhoven, but unfortunately, he does not know which one. Fortunately, he sees two twin-brothers standing at the road junction, and he decides to ask them for directions.

The traveler knows that one of the two brothers always tells the truth and the other one always lies. Unfortunately, he does not know which one always tells the truth and which one always lies.

How can the traveler find out the way to Eindhoven by asking just one question to one of the two brothers?

Answer 45

The question that the traveler should ask is: “Does the left road lead to Eindhoven according to your brother?” If the answer is “Yes”, the traveler should turn right, and if the answer is “No”, the traveler should turn left.

Explanation: There are four possible cases:

The traveler asks the question to the truth-telling brother, and the left road leads to Eindhoven. The truth-telling brother knows that his lying brother would say that the left road does not lead to Eindhoven, and so he answers “No”.
The traveler asks the question to the truth-telling brother, and the right road leads to Eindhoven. The truth-telling brother knows that his lying brother would say that the left road leads to Eindhoven, and so he answers “Yes”.
The traveler asks the question to the lying brother, and the left road leads to Eindhoven. The lying brother knows that his truth-telling brother would say that the left road leads to Eindhoven, and so he lies “No”.
The traveler asks the question to the lying brother, and the right road leads to Eindhoven. The lying brother knows that his truth-telling brother would say that the left road does not lead to Eindhoven, and so he lies “Yes”.