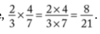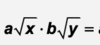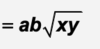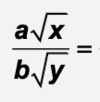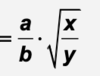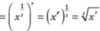Problem Solving Flashcards
What is the formula for circumfrence of a circle?
= 22/7 * diameter
What is a right triangle?
This is a triangle where one of the angles is a 90o angle.
In a triangle, across from which side do we find the widest angle?
We find this angle opposite the longest side.
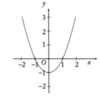
Describe the graph we use for coordinate geometry?
On this item,
y = verticle
x = horizontal
(0,0) = Origin
numbered counter clockwise
53 = ?
= 125
How do we deal with multiplying large fractions?
We use cross multiplication for this.
What do we call it when we take two fractions that are being multiplied, and divide the numerator in one and the denominator of the other by the same common divisor?
We call this cross multiplication.
n root of x =
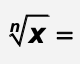
= x1/n
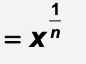
What is the decimal form of 1/4?
The decimal form of this fraction is 0.25.
What do we know if the sum of the digits of another number is divisible by one of these number, respectively?
This means that the number is divisible by 3 or 9, respectively.
What is the formula for rates of work done?
1/units of timea
+
1/units of timeb
=
1/units of timea+b
just make sure that 1 = the same job for both of them.
How do we find the y-intercept in coordinate geometry?
In coordinate geometry, we can find this by setting x to 0.
26
=?
= 64
What is the decimal form of 1/9?
The decimal form of this fraction is 0.1111….
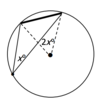
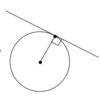
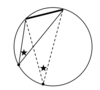
Two inscribed angles (in a circle) holding the same or two equal chords/arcs are ____.
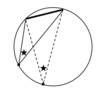
Two _____ in a circle holding the same or two equal chords/arcs are equal.
The ratio of the number a to the number b (b ≠ 0)
One form of notation for this is a:b or
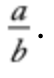
What is the formula for the volume of a cylander?
= 22/7*r2*h
What is a quotient?
This is a whole integer that a number is divisible by, usually with a remainder.
x-r =
= 1/xr
What is the formula to find the sum of all interior angles in a shape?
= [(sides)-2]*180
The probability that E does not occur is P(not E) = ____?
= l − P(E)
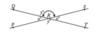
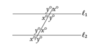
If a diagonal line is drawn intersecting two parallel lines, what will be true of the angles?
What is the formula for compound interest?
A=P(1+r/n)nt
What are the Pothagorean Triplets?
These are right triangles with “nice” integer side lengths, in set proportions:
3: 4:5
5: 12:13
7: 24:25
Root of xy = ?
= root of x * root of y
What is the formula for rate?
= distance or work done/time
What does b represent in the equation y = mx + b?
b represents the y-intercept in this equation.
What is a rhombus?
This shape has:
- 4 equal sides
- Opposite angles equal
- Opposite sides parallel
What is the decimal form of 1/5 ?
The decimal form of this fraction is 0.2.
What is a prime number?
This is a positive integer that has exactly two different positive divisors, 1 and itself.
What is the area of a quadrilateral?
=1/2(length of both bases added together)*(height)
multiplying fractions
The square root of a negative number is ______.
This square root is not a real number.
What can we set y to in order to solve for x in coordinate geometry?
This can be set to 0 in order to find x in coordinate geometry.
What is 0.321 as a fraction?
What is the area of an equilateral triangle?
The area of this triangle =
25 = ?
= 32
What is this called?
A Venn diagram.
This equation worked out into long form = ?
This equation simplified = ?
What is the formula for finding the distance gone at a certain speed?
= rate * time
What is the formula for compound interest?
A = P(1+r/n)nt
What is the decimal form of 1/3 ?
The decimal form of this fraction is 0.33333…
Odd + Even = ?
This addition results in an odd number.
What is a parabola?
This is the shape made by a quadratic function
If a triangle is inscribed in a circle such that the hypoteneuse is the diameter of the circle, what kind of triangle is it?
A right triangle would be inscribed in this shape with the hypoteneuse as the _____.
This equation simplifies to _____ ?
What is the long form of this equation ?
34 = ?
= 81
(xr)s=
xr*s = (xs)r
What is the square root of 2?
1.4 is the square root of this number.
24
= ?
= 16
What is the decimal form of 1/8?
The decimal form of this fraction is 0.125.
How do you multiply with decimals?
We do this by adding the number of these together and making sure there’s the same number of them in the answer.
In this formula, what do all the letters stand for?
A=P(1+r/n)nt
For this formula:
A= Amount at end of Time
P= Principal
r= interest rate (as a decimal)
n=number of times interest is compounded per unit t
t=time
How do we simplify messy fractions?
We do this by using prime factorization.
Is 1 a prime number? Why?
This is not a prime number because it only has one divisor.
A central angle is twice as large as an ____ angle holding the same chord/arc.
A ___ angle is twice as large as an inscribed angle holding the same chord/arc.
What are the “special” right triangles?
These have ratios of:
1:1:21/2
(45o, 45o, 90o)
1:31/2:2
(30o, 60o, 90o)
What is a chord?
A line segment with end points on a circle.
What is a mixed number
If the probability of two events >1, what do we know?
If this number =___ the events in question are not mutually exclusive.
What is the union of two sets
For any two sets A and B, the union of A and B is the set of all elements that are in A or in B or in both
Such an expression is called a second degree (or quadratic) polynomial in x, or third degree polynomial.
x2 + x + Constant=0
It is called this because x2.
It would be ___ degree if x3
a sum of terms that are each powers of x multiplied by coefficients.
A tangent line touches a circle at only one point. The line from the center to the point of tangency is ___ to the tangent line.
A tangent line touches a circle at only one point. The line from ______ is perpendicular to the tangent line.
24
= ?
= 16
27 = ?
= 128
What is the formula for the area of a triangle?
= (altitude)(base)
2
A fraction equals 0 if and only if___
if and only if its numerator equals 0
Odd x even
or
even x even
= ?
This multiplication results in an even number.
What is the area of a parallelogram?
= (length of altitude)*(length of base)
What is the formula for simple interest?
This is calculated using
I=PRT
Multiplying or dividing an inequality by a negative number does what?
Doing this reverses the order of the inequality.
How many sides in a polygon?
This shape has three or more sides, and is a closed plane figure that does not double back on itself.
What is the long form of this equation?
What is the simplified form of this equation?
The set of all allowable inputs for a function is called___?
____ is called the domain of the function.
The domain of any function can be arbitrarily specified, as in the function defined by “h(x) = 9x − 5 for 0 ≤ x ≤ 10.” Without such a restriction, the domain is assumed to be all values of x that result in a real number when substituted into the function.
How do we know if a number is divisible by four?
If this is true, the number created by the last two digits of the number in question will also be divisible by this number.
In this equation, what do n and k stand for?
In this equation,
n = the entire set
k = the number of objects chosen from the set, where order doesn’t matter.
28 = ?
= 256
This equation simplifies to___?
This equation can also be written as what ?
What is the maximum length of one side of a triangle?
This must be smaller than the sum of the other two sides of the triangle.
This equation simplifies to ___ ?
The long form of this equation = ?
what is the denominator
the bottom portion of a fraction
Dividing fractions
What is a rectangular solid?
It’s a 3D object made of 6 rectangular faces, where opposite faces have the same dimensions.
26
= ?
= 64
What is a factorial?
If n is an integer greater than 1, then _____ denoted by the symbol n!, is defined as the product of all the integers from 1 to n.
Denotes?
Line segment PQ is denoted by this shorthand.
x0 =
A number to this power = 1
What is the linear formula to find coordinates?
This formula is used for the operation in question.
y=mx+b
where b is a constant
What can we assume?
If this is true, we can assume that the top portion of this equation = 0.
What do we know if a number is divisible by both two and three?
If this is true then we know the number in question is divisible by 6.
What is a scalene triangle?
This triangle has three differently sized angles and sides.
How many degrees are in a circle?
360 degrees for this shape.
What is the formula for slope?
m = (y2 - y1) / (x2-x1)
rise
run
This equation for solving a quadratic works unless___?
This equation for ____ works
unless b2 − 4ac ≤ 0.
If b2 − 4ac = 0, then these two expressions for x are equal to -b/2a, and the equation has only one root.
If b2 − 4ac < 0, then is not a real number and the equation has no real roots.
Simplify xryr
This simplified =(xy)r
(xr)(xs) = ___?
= x(r + s)
Odd + Odd
or
Even + Even
= ?
This addition results in an even number.
What is the factorial of 0?
=1! = 1
What kind of triangle does the Pythagorean Theorum refer to?
This theorum refers to RIGHT TRIANGLES only.
(x/y)r=
=xr/yr
How do we calculate the number of elements in a union?
=|S| + |T| - |SΠT|
What is the formula for the surface area of a cylander?
= 2 (22/7 * r2) + 22/7*d*h
What is a vertex?
This is where 3 edges meet.
What is an equilateral triangle?
All sides and angles are equal on this type of triangle.
If E and F are independent, then P(E or F)=___
=P(E) + P(F) - P(E)P(F)
What is the formula for the area of a circle?
= 22/7 * r2
What are vertices?
These are points of intersection of a polygon.
If two lines intersect, the opposite angles ____?
if two lines intersect, these are called vertical angles and have the same measure.
The value of the probability when an event is certain to occur is ___?
The value of the probability of this event would be 1.
231 in scientific notation would be ___?
In scientific notation this would be 2.31 * 102.
What is the decimal form of 1/6?
The decimal form of this fraction is 0.166666…
54 = ?
= 625
How do we calculate the number of ways a set of objects can be ordered?
The factorial is useful for ____.
If a set of n objects is to be _____, then there are n choices for the 1st object, n − 1 choices for the 2nd object, n − 2 choices for the 3rd object, and so on, until there is only 1 choice for the nth object. Thus, by the multiplication principle, the _______= n!.
What does it mean if two linear equations have no common solution in coordinate geometry?
This means that the two lines represented by the equations are parallel, and don’t intersect.
What is the Pythagorean Theorum?
a2+b2 = c2
Where a and b are the shorter sides of a RIGHT triangle, and c is the longest side.
What do we know if the sum of the digits of a number is divisible by either of these two numbers?
If this is true we know the number itself is divisible by either 3 or 9 respectively.
What is the long form of this equation?
What is the simplified form of this equation?
x1/2 =
= power notation of the square root of x
How do we raise a fraction to a power?
(a/b)p
=
ap
bp
This equation simplifies to ___ ?
The long form of this equation = ?
What does fx = ?
This notation = y in coordinate geometry.
xr/xs=
=xr-s
What does tangent mean?
A line that has one point in common with a circle.
What is an isosceles triangle?
On this triangle, 2 of the 3 sides are equal, and their opposing 2 angles are equal.
What is the square root of 5?
2.2 is the square root of this number.
What does “circumscribed by” mean?
This means that something is around the object.
What is altitude?
This is a line drawn from the vertex to the opposite side (base), used to find the height of a shape.
How do we find standard deviation?
(1) find the arithmetic mean
(2) find the differences between the mean and each of the n numbers
(3) square each of the differences
(4) find the average of the squared differences
(5) take the nonnegative square root of this average
In a right triangle, where do we always find the hypotenuse?
In a right triangle, we always find this across from the right angle.
What is the intersection in a set?
The ______is the set of all elements that are both in A and in B
Even + even
or
odd + odd
= ?
This addition results in an even number.
How do we calculate the permutations of a set of objects? (ie: order matters)
To calculate this we use
n!/(n-k)!
Odd x odd = ?
This multiplication results in an odd number.
The probability that “E or F ” occurs is____?
The probability of this = P(E) + P(F) − P(E and F)
What is the square root of 3?
1.7 is the square root of this number.
What is radius?
1/2 diameter, or the centre of a circle to the edge of it.
What does this notation mean?
Absolute value
Even x even
or
Odd x even
results in?
These multiplications result in an even number.
= |x|
For any independent events E and F: P(E and F)=
= P(E)P(F)
What is the decimal form of 1/7?
The decimal form of this fraction is 0.14.
This equation factors out to ___ ?
This equation into long form = ?
How do we calculate median?
To calculate the____of n numbers, first order the numbers from least to greatest; if n is odd, the median is defined as the middle number, whereas if n is even, the median is defined as the average of the two middle numbers
The square root of a negative number is ___.
The square root of this is not a real number because ____.
what is the numerator
the top portion of a fraction
How do we find the length of an arc?
= (xo/360o) * (22/7*2r)
If two linear equations with unknown x and y have a unique solution, what does that mean, and what happens at this point?
This means that the two lines represented by the two equations intersect, at ____.
The value of the probability when there is no possibility of an event occuring = ___?
The value of the probability would be 0.
How many triangles in a pentagon?
This shape is made of three triangles.
If the order of selection is not relevant and only k objects are to be selected from a larger set of n objects, how do we calculate how many combinations we can get?
Every positive number n has ___ square root(s)?
Every ___ has two square roots, one positive and the other negative.
How do we calculate probability?
How do you divide with decimals?
If a quadratic equation ax2+bx+c=0 cannot easily be factored, how do we solve it?
When do we use this equation?
33 = ?
= 27
What is the trick for large numbers squared?
The trick for this equation is:
- Write down the square of the units digit.
- Multiply the number made by the leftover digits by the integer one greater and write that number down in front of the first number you wrote down.
If the numbers in a set are ______, then the mean and the median of that set are equal.
If the numbers in a set are equally spaced, then the mean and the median of that set are _____.
If m is the mean of n numbers, then the sum of the numbers is _____.
If m is the mean of n numbers, then the ____ of the numbers is nm.
When you’re on question #15 of Quantitative, you should have ____ minutes left on the clock.
When you’re on question ___ of Quantitative, you should have 34 minutes left on the clock.
When you’re on question #10 of Quantitative, you should have ____ minutes left on the clock.
When you’re on question ___ of Quantitative, you should have 44 minutes left on the clock.
When you’re on question #20 of Quantitative, you should have ____ minutes left on the clock.
When you’re on question ___ of Quantitative, you should have 24 minutes left on the clock.
How do we calculate % increase/decrease?
new - initial
initial
if a/b = c/d what else do we know?
if ?/? = ?/? we know that
a*d=b*c
(GCD of x and y)(LCM of x and y)=______
(____ of x and y)(____ of x and y)=x*y
What is the formula for circumfrence of a circle?
=22/7*Diameter
What is the formula to find the distance between two points on a graph?
43
=?
64
k(k-1)!
=?
This multiplication
=k!
How do we simplify a large fraction, or deal with a large division?
We can use factoring for this.
