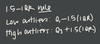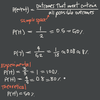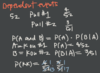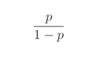Probability & Statistics Flashcards
What is one-way data?
Data that’s focused on or collected about just the single individual.
Variable data given for individuals.
One independent variable, called individuals, and one OR more dependent variables, called the variables
What does this graph represent?
Bar Chart
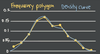
What does this graph represent?
Histogram
What does this graph represent?
Line graph
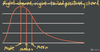
What does this graph represent?
Ogive
What is Two-way data?
Two independent categories on which the variables are dependent.
What is the relative frequency table?
A table that shows percentages instead of actual counts of outcomes of one experiment.
Displays data in Two-way or One-way tables as percentages.
What is Joint Distribution Table?
A table that compares two different distributions.
It helps us see a correlation between the two variables (distributions).
What is Marginal Distribution?
The Total row or the Total column in a Joint Distribution.
What is Conditional Distribution?
Distribution of one variable, given a particular value of the other variable.
What is the joint distribution section of this table?
The joint distribution or the joint probability distribution is the probability that a pair of events can happen. All of the possible pairs of events happen in the body of the table
What is the marginal distribution section of this table?
The marginal distribution comes from the total column OR total row.
What is the Frequency Table?
A table that displays how frequently or infrequently something appears.
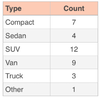
What is a dot plot?
Shows frequency of small datasets.
What is a Histogram
(or Frequency Histogram) ?
Just like a Bar Graph, except that we collect the data into buckets or bins, and then sketch a bar for each bucket.
Representation of the distribution of numerical or categorical data in bins.
What is a Stem Plot?
Data grouped together by the first digit(s) in each number.
The “stems” are the numbers on the left, in this case, the 6 and the 7.
The “leaves” are all the other numbers on the right.
What is Mean?
The average.
What is median?
The value in the middle when you line up all the data in order.
What is Mode?
The value that appears most often.
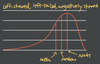
What do we need to look at first when we analyze data?
What is spread?
How and by how much a data set is spread out around its center.
We call measures of spread measures of dispersion or scatter.
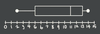
What is Range?
The difference between the largest and smallest value.
What is Quartile?
What is Interquartile range?
The difference between the median of the upper half
and the median of the lower half.
What happens to measures of central tendency and spread when we add/remove a constant value to every value in the data set?
Adding 6 to the entire data set also adds 6 to the mean, median, and mode, but the range and IQR stay the same.
What happens when we multiply our data set by a constant value?
What happens with the mean if we add a data point to our data set?
What do Outliers do to the mean and median of a data set?
Change Mean significantly, change Median slightly
Explain this plot.
What is population and sample?
Population is the entire group or all of the subjects in a population.
Sample is a subset of the population and we hope that it will be somewhat representative of the population as a whole.
Describe Mean, Variance, Standard Deviation,
biased/unbiased Sample Standard Deviation.
What is Frequency Polygon?
What is Density Curve?
Shows the distribution of the data when we increase the number of bins in a histogram to infinity.
Visualization of a distribution where the data points can take on any value in a continuum.
The area under the density curve is equal to 100 percent of all probabilities.
Draw a symmetric distribution.
Draw a Left Skewed Distribution
Draw a Right Skewed Distribution.
What should be used for measuring central tendency and spread if we have skewed data?
What is 1.5 - IQR Rule?
Describe Normal Distribution, Percentile, z-Score, z-Score tables (+/-)
Define simple probability of an “event”
What is the Probability Addition Rule (Sum Rule) and what does it make sure?
For mutually exclusive events the probability of
P(AuB) = P(A) + P(B)
For overlapping events, we don’t double-count the overlap.
P(AuB) = P(A)+P(B)-P(AandB)
Definition: Suppose some event E can occur in m ways and a second event F can occur in n ways, and suppose both events cannot occur simultaneously. Then E or F can occur in m + n ways.
What are Mutually exclusive (or disjoint) events?
Apply Probability Multiplication Rule to dependent events.
Give an example of a Dependent Event
Give an example of an Independent event
What is the Multiplication Rule?
If events A and B are mutually exclusive (independent),
the probability of event A happening and Event B happening on two separate trials is
P(A and B) = P(A) * P(B)
It’s giving us the probability that multiple independent events happen on consecutive trials.
For dependent events:
P(A and B) = P(A) * P(B|A)
Product Rule Principle: Suppose an event E can occur in m ways and, independent of this event, an event F can occur in n ways. Then combinations of events E and F can occur in m*n ways.
What is the formula for Bayes’ Theorem?
Use Tree Diagramm method for Bayes’ Theorem to calculate the probability that biased dice was chosen given 6 is already rolled. The biased die has a 50% chance of rolling a 6.
When should you use the Bayes’ Theorem?
When you have P(A|B) but want to find P(B|A)
Give formula for Conditional Probability.
The world around us is full of phenomena we perceive as random or unpredictable.
How do we model these phenomena? (How do we call them?)
Outcomes of some experiment.
What is Sample Space?
Sample Space = all possible outcomes
Sample space is set whose elements describe all outcomes of the
experiment in which we are interested.
The outcomes of some experiments are elements of a sample space Ω.
Sample space of the experiment of tossing of a coin is
Ω = {H, T }
What are Events?
Events are subsets of Sample Space Ω.
The events will be assigned a probability, a number between 0 and 1 that expresses how likely the event is to occur.
What is permutation?
The order in which n different objects can be
placed. This is called a permutation of the n objects.
There are
n · (n - 1) · · · · 3 · 2 · 1 = n!
possible permutations of n objects (taken all at the time).
What are disjoint events?
We call events A and B disjoint or mutually exclusive if A and B have no
outcomes in common; in set terminology: A∩B = ∅. For example, the event L
“the birthday falls in a long month” and the event {Feb} are disjoint.
What are Intersection, Union, Complement?
The set L∩R is called the intersection of L and R and occurs if both L and R
occur. Similarly, we have the union A∪B of two sets A and B, which occurs if
at least one of the events A and B occurs. Another common operation is taking
complements. The event Ac = {ω ∈ Ω : ω ∉ A} is called the complement of A;
it occurs if and only if A does not occur. The complement of Ω is denoted
∅, the empty set, which represents the impossible event.
What does it mean event A implies event B?
we say that event A implies event B if the outcomes of A also lie
in B. In set notation: A ⊂ B
A is a subset of B
What is probability function?
We want to express how likely it is that an event occurs. To do this we will
assign a probability to each event.
Since each event has to be assigned a probability, we speak of a probability function. It has to satisfy two basic properties.
What is the probability of a union?
For any two events A and B we have
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
What is probability of complement of event?
Suppose we throw a coin two times.
What is the sample space associated with this
experiment?
Ω = {H, T } × {H, T } = {(H, H), (H, T ), (T, H), (T, T )}
If we consider two experiments with sample spaces
Ω1 and Ω2, what is the sample space of the combined experiment?
The sample space of the combined experiment is the set
Ω = Ω1 × Ω2 = {(ω1, ω2) : ω1 ∈ Ω1, ω2 ∈ Ω2}
If Ω1 has r elements and Ω2 has s elements, then Ω1 × Ω2 has rs elements.
When we perform an experiment n times, what is the corresponding
sample space?
What are DeMorgan’s Laws?
What is the probability that neither E nor
F occurs?
What is the event “at least one of E and F occurs”?
the event E U F
What event is neither event 𝐴 nor event 𝐵?
What are the Distributive Laws?
What are the Associative Laws?
X \ Y = ?
(in terms of Y’)
X \ Y = X ∩ Yc
Laws of the Algebra of Sets
Idempotent Laws
A ∪ A = A
A ∩ A = A
Associative Laws
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Commutative Laws
A ∪ B = B ∪ A
A ∩ B = B ∩ A
Distributive Laws
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Identity Laws
A ∪ ∅ = A A ∪ U = U
A ∩ ∅ = ∅ A ∩ U = A
Involution Laws
(Ac)c = A
Complement Laws
A ∪ Ac = U A ∩ Ac = ∅
Uc = ∅ ∅c = U
DeMorgan’s Laws
(A ∪ B)c = Ac ∩ Bc
(A ∩ B)c = Ac ∪ Bc
Others
A \ B = A ∩ Bc
A = (Bc ∩ A) ∪ (B ∩ A)
A ∩ Bc = A ∪ B \ B
Additivity
P(A ∪ B ∪ C) = P(A ∪ B) + P(C) = P(A) + P(B) + P(C)
P(A) = P(A ∩ B) + P(A ∩ Bc) = P(B) + P(A \ B)
If the two events A and B are independent, what is P(A∩B) ?
P(A∩B) = P(A) * P(B)
If the two events A and B are overlapping, what is P(A∩B) ?
P(A∩B) = P(A|B) * P(B)
Give the formula for binomial coefficients. Calculate an example.
Note that (n Chose r) has exactly r factors in both the numerator and the denominator.
Give the Lemma 1 for binomial coefficients.
What is the formula for Permutation of n objects taken r at the time?
Permutation(n,r) = n! / (n-r)!
Give the formula for Permutations with Repetitions.
Permutation(n; n1, n2, …, nr)
We are looking for the permutation of n objects of which n1 are alike, n2 are alike, …, nr are alike.
Permutation(n; n1, n2, …, nr) = n! / n1! n2! … nr!
Suppose that we are given n distinct objects and wish to arrange r of these objects in a line.
what is the number of ordered samples with Replacement of size r?
r
|—————–|
n * n * n … n = nr
What is the number of ordered samples without Replacement of size r?
nPr = n! / (n-r)!
What is a Combination? Give an example.
Combination of n objects taken r at a time is any selection of r of the objects where order doesn’t count.
An r combination of a set of n objects is any subset of r elements.
This is denoted by
C(n,r) or nCr
Example: given set {a,b,c,d}
C(4,3) = 4!/(3!*1!)
abc, abd, acd, bcd
How do we calculate circular permutation?
(n-1)!
What is the expected value (mean) of a discrete random variable?
What is the variance of a discrete random variable?
What are Mean and Std.Dev. for combinations of random variables?
What is the formula for Probability of Binomial Random Variable?
What is the classical (A Priori) definition for the probability p of an event E?
Then p(E) = n(E) / n(S)
What is frequency (A Posteriori) definition for probabilty of an event?
Suppose after n repetitions, where n is very large,
an event E occurs m times.
Then p = m / n
What is Finite Equiprobable Space?
A probability space S where each point
is assigned the same probability.
P(A) = n(A) / n(S)
What is Finite Probability Space?
Let S be a finite sample space S = {a1, a2, …, an}.
A finite probability space is obtained by assigning to each point ai in S a real number pi called the probability of ai satisfying the following properties:
(i) each pi is nonnegative, that is pi >= 0
(ii) the sum of the pi is 1
The probability P(A) of an event A is defined as the sum of the probabilities of the points in A:
P(A) = Sum(P(ai)
What is the formula for odds that something happens?
What is a finite stochastic process?
A finite stochastic process is a finite sequence of experiments where each experiment has a finite number of outcomes with given probabilities.
What is Multiplication Theorem for Conditional Probability?
Show an example using a tree diagram.
