Probability & Combinatorics Flashcards
(25 cards)
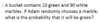

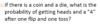

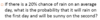

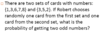

There are:
3 green marbles
2 red marbles
1 yellow marble
What is the probability of choosing a green OR yellow marble?
What does OR translate to?
There are 6 total marbles, so denominator is 6
OR translates to +
So, we add: 3/6 chance of green + 1/6 chance of yellow = 4/6 = 2/3
There are:
3 green marbles
2 red marbles
1 yellow marble
If we choose 2 marbles without replacement,
what is the probability of choosing a green AND a red?
What does AND translate to?
AND means we multiply the individual probabilities
There are 2 ways to get a green and a red:
A) 1st marble green, 2nd marble red:
3/6 * 2/5 = 1/2 * 2/5 = 1/5 (once we’ve picked one, there’s only 5 left)
B) 1st marble red, 2nd marble green:
2/6 * 3/5 = 1/3*3/5 = 1/5
Overall, we have (Green AND Red) OR (Red AND Green), so we add:
1/5 + 1/5 = 2/5
There are:
3 green marbles
2 red marbles
1 yellow marble
If we choose 2 marbles without replacement,
what is the probability of choosing 2 greens?
Choosing 2 greens means Green AND Green
AND means we multiply the individual probabilities
3/6 * 2/5 = 1/2 * 2/5 = 1/5
(after we’ve chosen one green, there’s only 2 out of 5 left)
There are:
3 green marbles
2 red marbles
1 yellow marble
If we choose 2 marbles with replacement,
What is the probability of choosing a yellow first, and then a red?
This one is with replacement, so the denominator stays at 6.
There is only 1 option, since it says yellow is first. (we can’t have red, then yellow)
1/6 * 2/6 = 1/18
There are 3 dogs and 2 cats.
If two are chosen at random, what is the probability that they will both be the same type?
Translate: AND is *, OR is +
2 ways: both dogs, OR both cats
(Dog AND Dog) OR (Cat AND Cat)
3/5 * 2/4 + 2/5 * 1/4 = 3/10 + 1/10 = 4/10 = 2/5
If we flip a coin 4 times, what is the probability of it landing on the same side on all 4 flips?
We could have all heads, OR all tails, so we add these 2 probabilities:
A) All heads: 1/2 * 1/2 * 1/2 * 1/2 = 1/16
B) All tails: 1/2 * 1/2 * 1/2 * 1/2 = 1/16
1/16 + 1/16 = 1/8
If there is a 40% chance of rain,
What is the probability that it will NOT rain on the first day, and rain on the second day
Express as a fraction
Probability of NOT A = 1 - Probability of A
Probability of NOT rain = 1 - 40% = 1 - 2/5 = 3/5
AND translates to multiply:
Not Rain * Rain = 3/5 * 2/5 = 6/25
There are 2 sets of cards with numbers:
Set A {1, 2, 4, 6, 9} and Set B {1, 2, 3, 5, 6, 8}
If Joe randomly chooses 1 card from each set,
what is the probability that the numbers multiplied together will be an even number?
There are 3 ways to get an even:
Even * Even
Odd * Even
Even * Odd
There’s only 1 way to get odd: Odd * Odd = Odd
So, it is easier to do 1 - Probability of Odd
Set A: 2/5 chance to get Odd (1 or 9)
Set B: 3/6 = 1/2 chance to get Odd (1, 3, or 5)
Chance of Odd AND Odd = 2/5 * 1/2 = 1/5
1 - 1/5 = 4/5
Two dice are rolled. If the sum of the numbers on the dice was 7, what is the probability that one of the dice showed a number greater than 4?
The possibilities are limited to those that give a sum of 7. (“IF the sum…)
Without this condition, there would be 36 total possibilities (6 for first die * 6 for second die)
List the possibilities:
1-6, 2-5, 3-4, 4-3, 5-2, 6-1
There are 6 total –> that’s the denominator.
4 have a number greater than 4.
4/6 = 2/3
What are Permutations?
Permutations are the number of ways to choose, when order matters.
Ex: How many different license plates can be made, using 3 DISTINCT letters, choosing from the letters A, B, C, D, E, F, G
Write out 3 “Slots”, one for each letter.
___ ___ ___
There are 7 possibilites for the first slot, then 6 possibilites for the 2nd slot, then 5 for the 3rd slot (because the letters must be distinct). We multiply them to find the total number of ways.
_7_ * _6_ *_5_ = 210
What are Combinations?
How are Combinations different from Permutations?
Combinations are the number of ways to choose, when order doesn’t matter.
We count similarly to Permutations, but then we must divide by the number chosen, Factorial.
Combinations are most commonly used for picking groups – See example below
We must divide by 3! because we have overcounted the same teams chosen in a different order.
Team ABC is the same as ACB, BAC, BCA, CAB, and CBA.

How many different teams of 3 can be made from 7 people?
35
When we are picking groups, order does not matter, so we need to divide:
(ABC is the same team as ACB, etc)

How many different license plates can be made,
using 3 DISTINCT letters,
choosing from the letters A, B, C, D, E, F, G ?
Here, the order matters, so we don’t divide by 3! (3 factorial)
Write out 3 “Slots”, one for each letter.
___ ___ ___
There are 7 possibilites for the first slot, then 6 possibilites for the 2nd slot, then 5 for the 3rd slot (because the letters must be distinct).
We multiply them to find the total number of ways.
_7_ * _6_ *_5_ = 210
The diagram shows the various paths along which a mouse can travel from point X, where it is released, to point Y, where it is rewarded with a food pellet. How many different paths from X to Y can the mouse take if it goes directly from X to Y without retracing any point along a path?

Permutations (we multiply the number of options for each slot/choice/fork)
There are 3 forks along the path: 2 choices for the first one, 2 for the second and 3 for the third.
Total # of ways is 2*2*3 = 12

How many different ways are there to create a code, using 3 DISTINCT digits, using only integers greater than 2 and less than 8?
Order matters, so this is a Permutations problem, so don’t divide
How many integers are greater than 2 and less than 8?
3, 4, 5, 6, 7 —> 5 digits
Slots method —> 3 slots —> _5_ * _4_ *_3_ = 60
If 4 people each shake everyone else’s hand one time, how many total handshakes are made?
Small numbers, so we could list them. (With larger numbers we would want the formula)
Name them: A, B, C, D. List the pairs:
AB, AC, AD
BC, BD
CD
Total = 6
General formula: 4 people * 3 handshakes made by each person / 2 (because we double counted each handshake–> each handshake is shared by 2 people. AB is the same as BA)

How many different codes can be made from the letters A A A B C?
There are 5 letters, and order matters
If they were all different letters, it would be:
5 * 4 * 3 * 2 = 120
When there are repeats, we divide by the # of repeats, Factorial
So, since there are 3 A’s, it is 120 / 3! = 120 / (3*2) = 20
How many different codes can be made from the letters A A A B B C?
There are 6 letters, and order matters
If they were all different letters, it would be:
6 * 5 * 4 * 3 * 2 = 720
When there are repeats, we divide by the # of repeats, Factorial
So, since there are 3 A’s and 2 B’s we need to divide by 3! and by 2!
720 / ( 3! * 2!) = 720 / (3*2*2) = 60
There are 6 women and 3 men. How many different teams of 2 women and 2 men are possible?
Count the women pairs and men pairs separately, then multiply for the total.
Women: 6 * 5 / 2 = 15
Men: 3 * 2 / 2 = 3
15 * 3 = 45

5 athletes are competing for gold, silver and bronze medals, plus 1 honorable mention. How many different ways can the awards be distributed?
This time, the order matters, so we don’t divide by “4!”
4 Slots (for gold, silver, bronze, honorable mention) –> 5*4*3*2 = 20*6 = 120



