Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

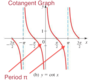
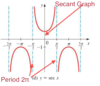
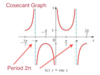
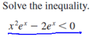Temple Midterm 2 Precalculus > Precalculus Midterm 2 > Flashcards

Precalculus Midterm 2 Flashcards

1
Q

Properties of Natural Logarithms

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

the Natural Logarithmic function is the inverse of the natural exponential function

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Graph of the Natural Logarithmic Function

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

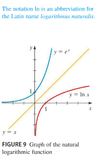
Natural Logarithms

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Common Logarithms

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Graph of the Family of Logarithmic Functions

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Graphing a Logarithmic Function by Plotting Points

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Inverse Function Property Domain

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

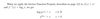
Inverse Property Function

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

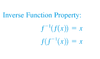
Log to Exponential Form

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Omitting the Parenthesis

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Definition of the Logarithmic Function

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

4.3 Definition of Logarithmic Functions

video

http://college.cengage.com/mathematics/blackboard/shared/content/video_explanations/video_wrapper.html?filename=kazmierczak/srwp60403a&title=Logarithmic%20Functions%20I

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Since Logarithms arw exponents the Laws of Exponents give Rise to the Laws of Logarithms

http://college.cengage.com/mathematics/blackboard/shared/content/video_explanations/video_wrapper.html?filename=kazmierczak/srwp60404&title=Laws%20of%20Logarithms

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Expanding and Combining Logarithmic Expressions

PG 355

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

WARNING There is no corresponding Logarithm Rule for of a Sum or a Difference

pg 356

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Change of Base Formula Explanation

pg 357

http://college.cengage.com/mathematics/blackboard/shared/content/video_explanations/video_wrapper.html?filename=kazmierczak/srwp70404&title=Change%20of%20Base%20Formula

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

Another Way to Look at the Change of Base Formula

pg 357

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

http://college.cengage.com/mathematics/blackboard/shared/content/video_explanations/video_wrapper.html?filename=kazmierczak/srwp60405&title=Exponential%20Equations

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

4.5 Guidlines for Solving Exponential Equations

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Solving an Exponential Equation by isolating the exponential term

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

When x is on both sides of the exponent

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

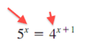
When x is in the denominator of an exponential equation

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

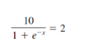
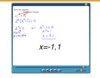
When an exponential equation is a quadratic equation

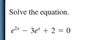
It must be factored

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

4.5 When the Exponential Equation has A Common Factor

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

4.5 Solve the Logarithmic Equation for x

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

4.5 Using the Quadratic Equation to Solve a Logarithmic Equation

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q
  1. 5 Exponential Equation Inequality
    https: //www.webassign.net/v4cgi/extra/bc_enhanced/index.tpl?asset=watch_it_player&asset_url=/bc_enhanced/sprecalc7_w_player/scolalg5_05_04_070.html&UserPass=40416dd1f85ab2d92f82bfef24bd5be5
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q

http://college.cengage.com/mathematics/blackboard/shared/content/video_explanations/video_wrapper.html?filename=kazmierczak/srwp70405&title=Compound%Interest

A
30
Q

get it from book problems pdf

A
31
Q
A
32
Q

Positive and Negative Angles are determined by the movement of the terminal side away from the initial side

clockwise-negative

counter clockwise-positive

A
33
Q

How Radians (the preferred angle measure in calculus) are measured

A

Note the arc created by the line is the same length as the line or 1 radian

34
Q
  1. 1 Converting between Radians and Degrees
    https: //www.webassign.net/v4cgi/extra/bc_enhanced/index.tpl?asset=watch_it_player&asset_url=/bc_enhanced/sprecalc7_w_player/sprecalc6_06_01_005.html&UserPass=bd5ee596620b98562a811b6665bca489

and

https://www.webassign.net/v4cgi/extra/bc_enhanced/index.tpl?asset=watch_it_player&asset_url=/bc_enhanced/sprecalc7_w_player/sprecalc6_06_01_017.html&UserPass=bd5ee596620b98562a811b6665bca489

A
35
Q

Angles in standard position all start (initial side) on the positive x axis

A
36
Q

Coterminal Angles-have the same initial and terminal sides just have more rotations of 360° or 2π

https://www.webassign.net/v4cgi/extra/bc_enhanced/index.tpl?asset=watch_it_player&asset_url=/bc_enhanced/sprecalc7_w_player/sprecalc6_06_01_035.html&UserPass=bd5ee596620b98562a811b6665bca489

A

Positive Coterminal Angles add multiples of 360° or 2π

Negative Coterminal Angles subtract multiples of 360° or 2π

37
Q

Interactive Unit Circle

A

https://www.mathsisfun.com/algebra/trig-interactive-unit-circle.html

38
Q

The Unit Circle Cosine,Sine

A
39
Q

Trigonometry of right Triangles-

The Special Two Triangles to Remember

http://college.cengage.com/mathematics/blackboard/shared/content/video_explanations/video_wrapper.html?filename=kazmierczak/srwp70602&title=Trigonometric%20Ratios%20and%20Special%20Triangles

A
40
Q

The Trigonomic Ratios to Remember

A
41
Q

SOHCAHTOA

A
42
Q

The Reciprocal Relations in Trig

Cosecant

Secant

Cotangent

A
43
Q

Height of a Building

Angle of Elevation

Angle of Depression

Line of Sight

A
44
Q

Height of a Tree

A
45
Q

Fundemental Identities of Trig

A
46
Q

Definition of Trigonomic Functions

A
47
Q

All Students Take Calculus

A

All Students Take Calculus

48
Q

see page 494

A
49
Q

Periodic Properties of Sine and Cosine

Sine of t

or Cosine of t

remain the same as you ad 2∏ periods

A
50
Q

Graph of the unit circle values

http://college.cengage.com/mathematics/precalculus/animations/stewart/sp060503f02.html

A

Note the color pattern as the circle stretches along the line as one period of 2∏

51
Q

One period of y=sin t

0≤ t ≤2∏

A

Graph of sin t for

0≤ t ≤2∏

52
Q

One period of x=cosine t

0≤ t ≤2∏

A

Graph of cos t for

0≤ t ≤ 2∏

53
Q

Vertical transformaton of Cosine Curve

A

Vertical transformaton of Cosine Curve by +2

54
Q

5.3 Reflection of a Cosine Curve

A

Reflction of a cosine curve -cos

55
Q

Vertical Stretching and Shrinking of a Sin Graph

AMPLITUDE is the true Value of the number in front of the sin or cos

⎢a⎥sin

A

The Higher the number the higher the peaks

y=2 sin x

Fractions cause Flatter Graphs

y=1/2 sin x

56
Q

Finding the Period of Sine and Cosine Curves

period=2∏/k

A
57
Q

https://www.webassign.net/v4cgi/extra/bc_enhanced/index.tpl?asset=watch_it_player&asset_url=/bc_enhanced/sprecalc7_w_player/sprecalc6_05_03_043.html&UserPass=44b63ef21500978162e459f571f147ab

A

From the graph the period =2π

so

2π/k=2π

k=1

58
Q

Horizontal Shift on a Graph

Remember it is the part (x-b)

and is a shift in an Unexpected Direction

this affects x so it is in the parenthesis with x

A
59
Q

Inverse Sine Function

A
60
Q

Inverse Cosine Function

A
61
Q

Inverse Tangent Function

A
62
Q

Periodic Properties of

tan

cot

sec

csc

A
63
Q

Tangent Graph crosses the origin and swings to the right

A
64
Q

The Cotangent graph does not cross the origin and swigs to the left

A
65
Q

The secant graph has a period of 2π and looks like a U straddling the y axis

A
66
Q

The Cosecant Graph looks like a U between 0 and π in the first quadrant

with a period of π

and is an upside down U in quadrant 2

A
67
Q

Tangent and Cotangent figuring the period

π/k

A
68
Q

The secant and cosecant period is 2π/k

A
69
Q

Reciprical identities

Pythagorean Identities

Even odd Identities

Cofunction Identities

A
70
Q

Addition and Subtraction Formulas

A
71
Q

Double Angle Formulas

A

Temple Midterm 2 Precalculus (1 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions