Pre-Calc Exam 1 Flashcards
Find y-intercept(s) and x-intercept(s) of y = 2(x^2) - x - 1
y-intercept: (0, -1) x-intercepts: (-1/2, 0) and (1, 0)
Find y-intercept(s) and x-intercept(s) of y = 3(x^2) - 12
y = 3(x^2) +0x - 12 y-intercept: (0, -12) x-intercepts: (2, 0) and (-2, 0)
Find y-intercept(s) and x-intercept(s) of y = x + 3
y-intercept: (0, 3) x-intercept: (-3, 0)
Find y-intercept(s) and x-intercept(s) of y = (x^2) + 6x + 9
y-intercept: (0, 9) x-intercept: (-3, 0)
Find y-intercept(s) and x-intercept(s) of y = 3(x^2) + 18x + 27
y-intercept: (0, 27) x-intercept: (-3, 0)
Find y-intercept(s) and x-intercept(s) of y = x^2 + 4x + 5
y-intercept: (0, 5) x-intercept: 0 = x^2 + 4x + 5 x = [-b +/- sqrt(b^2 -4ac)]/2a x = [-2 +/- sqrt(2^2 -4*1*5)]/(2*1) = [-2 +/- sqrt(4-20)]/2 therefore, x-int = undefined
Find the inverse function of f(x) = 2x + 3
f(x) = y = 2x+3 y -3 = 2x (y-3)/2 = x [f(x)-3]/2 = f’(x)
Find the inverse function of f(x) = x + 1
f(x) = y = x + 1 y = x + 1 y-1 = x f(x) - 1 = f’(x)
Find the inverse function of f(x) = 2(x^2) - x -1
f(x) = y = 2(x^2) - x -1 y = 2(x^2) - x - 1 y + 1 = 2(x^2) - x (y + 1)/2 = (x^2) - (x/2) + (1/4) (y+1)/2 + 1/4= (x+ 1/2)^2 sqrt[(y+1)/2 + 1/4] = sqrt[(x+ 1/2)^2] sqrt[(y+1)/2 + 1/4] = x+ 1/2 sqrt[(y+1)/2 + 1/4] - 1/2 = x sqrt{[f(x)+1]/2 + 1/4} - 1/2 = f’(x)
Find the inverse function of f(x) = x^2 + 6x + 9
f(x) = y = x^2 + 6x + 9 y = x^2 + 6x + 9 y = (x+3)^2 sqrt(y) = sqrt[(x+3)^2] sqrt(y) = x + 3 sqrt(y) - 3 = x sqrt[f(x)] - 3 = f’(x)
Find the inverse function of f(x) = x^2 -12x + 36
f(x) = y = x^2 -12x + 36 y = x^2 -12x + 36 y = (x-6)^2 sqrt(y) = sqrt[(x-6)^2] sqrt(y) = (x-6) sqrt(y) + 6 = x sqrt[f(x)] + 6 = f’(x)
Find the inverse function of f(x) = 3(x^2) + 5x + 25
f(x) = y = 3(x^2) + 5x + 25 y = 3(x^2) + 5x + 25 y - 25 = 3(x^2) + 5x (y - 25)/3 = [3(x^2) + 5x]/3 (y - 25)/3 = (x^2) + 5x/3 (y - 25)/3 + [(5/3)/2]^2 = (x^2) + 5x/3 + [(5/3)/2]^2 (y - 25)/3 + (5/6)^2 = (x^2) + 5x/3 + (5/6)^2 (y - 25)/3 + 25/36 = (x^2) + 5x/3 + 25/36 (y - 25)/3 + 25/36 = (x + 5/6)^2 sqrt[(y - 25)/3 + 25/36] = sqrt[(x + 5/6)^2] sqrt[(y - 25)/3 + 25/36] = x + 5/6 sqrt[(y - 25)/3 + 25/36] -5/6 = x sqrt{[f(x) - 25]/3 + 25/36} -5/6 = f’(x)
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 1. The solution to the equation 3x − 2 = 4 is x = 7/2
False because the solution to the equation 3x − 2 = 4 is x = 2.
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 2. The solutions to the equation x^2 − 3x + 2 = 0 are x = 2 and x = −1.
(x-1)(x-2)=0 x=1, 2 Therefore, false. The solutions to the equation x^2 − 3x + 2 = 0 are x=1 and 2.
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 3. The zeros of f (x) = x^2 + 2x − 4 are irrational numbers.
f(x) = (x^2 +2x) -4 f(x) = (x^2 + 2x +1) - 4 + 1 f(x) = (x-1)^2 -3 (x-1)^2 - 3 = 0 (x-1)^2 = 3 sqrt[(x-1)^2] = sqrt(3) x-1 = sqrt(3) x = sqrt(3)+1 Therefore, true.
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 4. The zeros of f(x) = 2(x^3) − x^2 − x are rational numbers.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 5. The solution set of the inequality 2x + 1
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 6. The solution set of the inequality −3x + 4 ≥ 10 is the interval (−∞,−2].
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 7. The only solution to |3x − 4| = 2 is x = 2/3.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 8. The solution set of the inequality |x − 4| ≤ 3 is the interval [1, 7].
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 9. If |x − 5| = 3, then the distance from x to 5 is 3.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 10. If |2x − 5| = 3, then the distance from x to 52 is 32.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 11. The domain of the function f (x) =sqrt(x − 3) is [−3,∞).
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 12. The domain of the function f (x)= xsqrt(x − 3) is [3,∞).
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 13. The domain of the function f(x)= sqrt[(x +1)(x −2)] is (−∞,−1] ∪ [2,∞).
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 14. The domain of the function f(x) = sqrt(x^2 + x − 2) is (−∞,−2] ∪ [1,∞).
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 15. The center of the circle (x − 2)^2 + y^2 = 4 is (2, 0) and the radius is 4.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 16. The center of the circle x^2 + 2x + y^2 − 4y = 4 is (1, 2) and the radius is 3.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 17. The slope of the line 2x − 3y = 4 is −23.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 18. The lines x + y = 2 and 3x −2y = 1 intersect at the point (2, 1).
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 19. The lines −3x + 2y = 5 and 4y = 6x + 7 are perpendicular.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 20. The lines x − 3y = 3 and 4x − 6y = 5 are parallel.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 21. The lines 2x + y = 2 and 2y + x = −1 are perpendicular.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 22. The lines x + 2y = 1 and −2x + y = 3 are parallel.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 23. The equation of the line that has slope −3 and passes through the point (0, 1) is y = −3x − 1.
Answer
Opposite of exponents/how do you undo an exponent
By taking the root of that power. For example, to undo a square, take the square root. To undo a cube, cube root it.
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 24. The equation of the line that passes through the two points (2, 1) and (−3, 2) is 5y − x = 7.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true. 25. The shaded region is described by y ≤ 1.
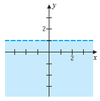
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The region outside the shaded region is described by
y > 1.
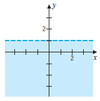
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The shaded region is described by 0 ≤ x < 2.

Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The region outside the shaded region is described by
x < 0 or x ≥ 2.
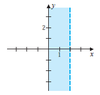
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The shaded region is described by |x − 1| ≤ 3 and
|y + 1| < 2.
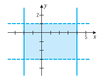
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The region outside the shaded region is described by
|x − 1| > 3 and |y + 1| ≥ 2.
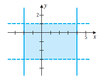
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The vertex of the parabola y = x2 + 4x + 3 is at (−2,−1).
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
32. The parabola y = −(x + 1)^2 − 2 has a maximum point at (−1, 2).
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The domain of the function is (−∞,−1) ∪ (−1, 1) ∪ (1,∞).

Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The range of the function is (−∞, 0] ∪ (2,∞).
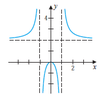
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The difference quotient for the function f (x) = −2x + 3 reduces to −2.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The difference quotient for the function f (x) = −2x + 3 reduces to −2.
Answer.
Determine whether the statement is true or false. If false, describe how the statement might be changed to make
it true.
- The difference quotient for the function
f (x) = x^2 + 2x − 1 reduces to 2x + 2 + h.
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The graph of an even function is symmetric with
respect to the origin and the graph of an odd function
is symmetric with respect to the y-axis.
Answer
Determine whether the statement is true or false. If false, describe how the statement might be changed to make it true.
- The graph of y = −f (x) is the reflection of the
graph of y = f (x) about the y-axis.
Answer
Find the solutions of x in
0 <= (4-x)sqrt(5-x)/{x sqrt[(x+4)(x-1)^1/3]}
AND write out the solutions of x as an inequality and as an interval notation.
Answer

y=a[sin(b(x-h))]+k, where
k= center line,
a=height of both directions, and
h=shift to the right or left
Y=-0.5sin(2x-3.14/4)+2
Find: vertical shift, horizontal shift, amplitude, reflection, period, period 1 start, period 1 end, period 2 start and period 2 end, minimum, and maximum


