Potentials

Question 1

If a conductor is “grounded”, that means…

Answer 1

…the voltage inside the conductor is zero.

Question 2

If you want to find the voltage inside a hallow, grounded conducting sphere, how come you can begin the integration at the conductor’s shell instead of infinity?

Answer 2

The voltage is defined as zero at the conductor’s shell, so there is no need to integrate starting father out than that.

Question 3

If you have two concentric conducting spheres, one inside the other, and the inside one has a positive charge on it, what will happen to the outer sphere?

Answer 3

A negative charge will be induced on the inside surface of the outer sphere, and a positive charge induced on the outside surface. The positive charge on the outside “communicates” the presence of the inner charge to the external world.

Question 4

Can an electric field exist between in the space between conductors?

Answer 4

Yes, absolutely. This is what a capacitor is.

Question 5

With two concentric spherical conducting shells, one inside the other, and the inside one with positive charge on it, there is a negative charge induced on the inside surface of the outer conductor. But we know that E inside a conductor must be zero, so what is going on here?

Answer 5

E inside the conductor is indeed zero, but is non zero at the exact radius of the inner surface.

Question 6

If you have a conductor with two cavities in it, and you place charges in those cavities, what force do the charges exert on each other?

Answer 6

None! The charges are shielded from each other by the conducting material in between them.

Question 7

If you have a conductor with two cavities in it, each with some positive charge inside, the charges cannot see eachother (they are shielded from eachother). Can the charges be seen from the outside of the conductor?

Answer 7

Yes! The presence of the charges is still communicated via an induced charge on the surface of the conductor that will be equal to the total charge placed in both cavities.

Question 8

When is a region shielded by a conductor, in general?

Answer 8

When the region is entirely surrounded by the conductor.

Question 9

Suppose you have a conductor with a cavity inside it, and you place a point charge next to the conductor. Does the point charge affect the field inside the cavity?

Answer 9

No. The cavity is shielded from external fields because it is completely surrounded by the conductor. The inverse is not true, however—if there were charge in the cavity, the external point charge would be affected by it, since the external point charge is not surrounded by a conductor.

Question 10

Does the shape of a cavity inside a conductor affect how well the cavity is shielded from external electric fields?

Answer 10

No.

Question 11

If you place a positive point charge next to a conducting sphere, what will happen?

Answer 11

A negative charge will be induced on the the side of the sphere closest to the point charge, and a positive charge will be induced on the side furthest from the point charge.

Question 12

If a charge is shielded from external charges by a conductor surrounding it, does that mean external charges are shielded from the charge inside the conductor as well?

Answer 12

No. The presence of the charge inside is communicated externally by the conductor. In general, shielding is a one-way street: it makes things enclosed by conductors oblivious to what is outside, but not the other way around.

Question 13

Does the location of a charge within a cavity in a conductor affect how the conductor appears to an external observer?

Answer 13

No. The charge distribution on the outside surface of the conductor will remain the same no matter what happens to the cavity.

Question 14

Does the location of a charge within a cavity in a conductor affect how charge is induced on the conductor?

Answer 14

On the inside surface of the conductor, yes—but on the outside surface, no.

Question 15

The distribution of charge on the outer surface of a conductor is dependent on A) the shape of the cavity in the conductor, B) the shape of the conductor, or C) Both.

Answer 15

B. The charge distributed on the outer surface of a conductor is determined by the shape of the conductor, not the shape of the cavity inside it.

Question 16

How does the charge distributed on the outer surface of a conductor relate to the charge within its cavities?

Answer 16

The charge distributed on the outer surface of a conductor is equal to the net charge within its cavities.

Question 17

What is Poisson’s equation?

Answer 17

Question 18

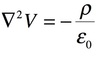
The Laplace Equation is…

Answer 18

Poisson’s Equation for a region where the charge density “rho” is equal to zero.

Question 19

Is Poisson’s/Laplace’s equation linear?

Answer 19

Yes, meaning solutions can be superimposed on eachother to give another valid solution.

Question 20

What is the graphical intuition behind the Laplace Equation?

Answer 20

The Laplace Equation says that the voltage at any point must be the average value of the voltage on a spherical surface centered at that point.

Question 21

According to Laplace’s Equation, can the voltage have a local maximum or minimum?

Answer 21

Only at the boundaries of the region. Otherwise, the average voltage on a spherical surface around the maximum or minimum would not be equal to the voltage at the center.

Question 22

What is the first uniqueness theorem of Poisson’s Equation?

Answer 22

The potential in a volume is uniquely determined if the charge density within region and the value of the potential on all the boundaries are specified.

Question 23

What is the fundamental principle behind the method of images?

Answer 23

The first uniqueness theorem of Laplace’s Equation: if you can guess a solution that satisfies all the boundary conditions and has the same charge density in the valid region, then that must be the correct solution.

Question 24

What is the method of images used for?

Answer 24

To find the potential in the region between a charge configuration and a grounded conducting plane. Normally this is very difficult because of the induced charge on the conductor.

Question 25

Explain the basic idea of the method of images.

Answer 25

If you have some charge configuration above a conducting plane, you can find the potential above the conductor (called the ‘valid region’) by pretending there are imaginary “image” charges of the opposite sign below the conductor. It just so happens that this will produce a plane of zero voltage—hence satisfying the boundary conditions for the valid region, and thereby giving the correct potential function in the valid region.

Question 26

Does the method of images work on finite conductors?

Answer 26

No, the conducting planes need to be infinite for the image method to work.

Question 27

Does the potential function found using the image method specify the potential below/within the conductor?

Answer 27

No, this is not the valid region—the Laplace equation does not have the same solution in this region.

Question 28

In the method of images, are you allowed to place an image charge in the valid region?

Answer 28

No, because then you are solving a different problem!

Question 29

In the method of images, the angle between two conductors is called…

Answer 29

…the “conductor plane angle”

Question 30

Which conductor configurations can the method of images be used for?

Answer 30

Configurations in which the conductor plane angle divides 360 degrees cleanly into an integer.

Question 31

What is the “polygon rule” in the method of images?

Answer 31

A real charge and its corresponding image charges will form an equi-angular polygon centered at the intersection of the conductor planes.

Question 32

If a charge is equidistant from two intersecting conductor planes, it (together with its image charges) will form a _______ polygon.

Answer 32

The charges will form a regular polygon, with uniform side lengths.

Question 33

If a charge is not equidistant from two intersecting conductor planes, it (together with its image charges) will form a _______ polygon.

Answer 33

The charges will form an irregular polygon, with varying side lengths. Note that irregular polygons are still equi-angular (all the angles are the same still).

Question 34

In the image method, is the net image charge always equal and opposite the net real charge?

Answer 34

No, the real & image charges are always opposite but not necessarily equal in magnitude (a spherical conductor is one scenario in which the magnitudes are not equal).

Question 35

In the method of images for a charge next to two intersecting conductor planes, what are the signs and magnitudes of the image charges?

Answer 35

The image charges alternate negative-positive-negative-positive etc etc, each equal in magnitude to the real charge. The image charges closest to the real charge should be opposite in sign.

Question 36

What is the formula for the number of image charges required to simulate a charge next to two intersecting conductor planes?

Answer 36

360 degrees divided by the conductor plane angle gives the number of total charges, so that minus one is the number of image charges.

Question 37

In the image method, in a scenario one real charge next to two intersecting conductor planes, can the number of image charges be even?

Answer 37

No, because otherwise they would have no net charge. The number of image charges per real charge must be odd.

Question 38

Consider a positive charge that is placed equidistantly between two conductor planes which intersect, forming a 60 degree angle. Describe the image charge configuration.

Answer 38

There will be 5 image charges, which, when combined with the one real charge, form a regular (equilateral) hexagon centered at the point where the conductors intersect. There will be 3 negative and 2 positive image charges. The image charges closest to the real charge will be negative.

Question 39

How can the image method be used to find the amount of induced charge on a conducting plane?

Answer 39

The image method gives the potential function in the valid region. The surface charge density of a conductor is dependent on the derivative of this potential function. The charge density can then be integrated over the conducting plae.

Question 40

Can the method of images be used to solve situations with multiple real charges?

Answer 40

Yes, you just need to draw the image charge configuration for every real charge and draw all the image charges at once.

Question 41

Can the method of images be used for a charge next to a conducting sphere?

Answer 41

Yes, but there are different conventions for drawing the image charge(s).

Question 42

Where (in general) is the image charge placed in a scenario that has a real charge near a conducting sphere?

Answer 42

The image charge is placed on the line going from the center of the sphere to the real charge. In general, the image charge is not at the center of the sphere.

Question 43

When a charge is near a grounded conducting plane, what is the force felt by the conducting plane?

Answer 43

The conducting plane is pulled toward the real charge with the same force that real charge would be pulled by the imaginary charge (due to Newton’s third law). The average distance from the induced charges to the real charge is equal to the distance from the imaginary charge to the induced charge.

Question 44

How do you model a charge near a non-grounded conducting sphere using the image method?

Answer 44

In addition to the normal (off-center) image charge for a sphere, use another image charge at the center of the sphere, which will raise the potential at the surface of the sphere.

Question 45

Can you approximate a conducting sphere with a point charge if it is next to a grounded conducting plane?

Answer 45

No, because the conducting sphere constrains field lines to remain perpendicular to its surface, while a point charge allows the field lines to bend toward the conductor freely.

Question 46

How is solving the Laplace equation using separation of variables similar to using the image method?

Answer 46

They both utilize the uniqueness theorem of the Laplace equation—if a solution satisfies all the boundary conditions and satisfies the equation within the valid region, it is the unique solution.

Question 47

A charge is placed near a non-grounded conducting sphere. How do you find the voltage at the sphere’s surface?

Answer 47

The voltage at the sphere’s surface will be as if the image charge were at the center of the sphere and had the same sign as the real charge.

Question 48

How do you draw the irregular polygon that is formed by the image charges when a real charge does not exactly bisect the conductor plane angle?

Answer 48

Draw the two image charges that are closest to the real charge (just like you would with a single conducting plane). Then, connect the three charges. The shape made by this connection will be the shape that is repeated in the irregular polygon.

Question 49

In a Laplace Equation “Brute force” problem, what are you given, and what is the goal?

Answer 49

You are given the physical scenario—e.g. the dimensions of some conducting box and the voltages of each side—and the goal is to find an exact potential function for the region inside the box.

Question 50

What is the first step to solving the Laplace Equation by brute force?

Answer 50

Write down and number the boundary conditions—you should have at least two for each dimension.

Question 51

If your final solution to the Laplace Equation has arbitrary coefficients in it…

Answer 51

…then it is not the exact solution for the scenario (and is useless)

Question 52

What does “separation of variables” refer to in the context of partial differential equations?

Answer 52

The technique in which you assume the solution is the product of independent equations of each variable, e.g: V(x,y) = V_x(x)V_y(y)

Question 53

When solving the Laplace Equation, what do you do after you have written down the boundary conditions?

Answer 53

Separation of variables. Assume V = V_x(x)V_y(y)V_z(z), plug that into Laplace’s equation, and group terms of the same variable.