PM: Risk and Return 2

Question 1

Combining risk free and risky assets =

Answer 1

Question 2

The optimal CAL (capital allocation line) =

Answer 2

best CAL is the one that offers the most preferred set of possible portfolios in terms of their risk and return.

different expectations of expected returns, standard deviations and correlation between risky assets will lead to different optimal risky asset portfolios and CALs.

Question 3

Homogeneous expectations =

Answer 3

a simplifying assumption of modern portfolio theory is HOMOGENEOUS EXPECTATIONS - regarding expected returns, standard deviation and correlations.

as a result, all investors face the same EFFICIENT FRONTIER and have the same OPTIMAL RISKY PORTFOLIO and CAL

Question 4

Optimal risky portfolio and CAL (given homogeneous expectations) =

Answer 4

optimal CAL is tangent to the efficient frontier.

all investors use the SAME PORTFOLIO OF RISKY ASSETS

but may choose different weights of risk free/risky assets

Question 5

market portfolio (of risky assets) and the Capital Market Line =

Answer 5

all investors hold the same risky portfolio, the MARKET PORTFOLIO of all risky assets.

the optimal CAL for all investors is the CAPITAL MARKET LINE

along which EXPECTED PORTFOLIO RETURN is a LINEAR function of PORTFOLIO RISK

Question 6

Capital Market LIne Equation =

Answer 6

y int: Rf, risk free rate

Slope: [E(Rm)-Rf]/SDm

so that if an investor takes no risk, SDp=0, the return is the risk free rate.

We can rearrange to get the below.

The investor will receive one unit of the market risk premium for accepting one unit of market risk, SDm.

Question 7

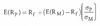
Borrowing and Lending portfolios =

Answer 7

Simple assumption that investors can both lend (invest) and borrow at the risk free rate - this means they can be invested at below or above the MARKET PORTFOLIO.

E(Rp) = Wm x E(Rm) + (1-Wm) x Rf

SDp = Wm x SDm

Question 8

The market portfolio and active vs passive mgmt =

Answer 8

Those who think markets are not informationally efficient, and think their values/prices are more ‘correct’ than the market, will invest actively and not simply invest in the market portfolio.

an active manager will over and under weight securities based on their evaluation of value/price.

Question 9

Systematic vs unsystematic risk =

Answer 9

the market portfolio contains all risky assets/has reduced all risk that can be reduced through diversification.

this is UNSYSTEMATIC RISK (unique, diversifiable, firm-specific)

this leaves SYSTEMATIC RISK (non diversifiable, market risk)

both portfolios and individual securities can have unsystematic and systematic risk

TOTAL RISK = SYSTEMATIC RISK + UNSYSTEMATIC RISK

Question 10

Risk vs # of portfolio assets =

Answer 10

Risk decreases at a decreasing rate when more securities are added to the portfolio - at a point the standard deviation will remain constant (12-18, 30, the number depends on the study)

Question 11

Systematic Risk and the cost of diversification =

Answer 11

Capital market theory says

• equilibrium security returns don’t depend on total risk/SD, they depend on systematic risk
• Diversification is FREE
• thus, investors will not be compensated for unsystematic risk that can be reduced throught FREE DIVERSIFICATION

SYSTEMATIC RISK: is measured by the contribution of a security to risk in a well diversified portfolio

EXPECTED EQUILIBRIUM RETURN FOR A SECURITY WILL DEPEND ON ITS SYSTEMATIC RISK

Question 12

Return generating and multi factor models =

Answer 12

RETURN GENERATING MODELS are used to estimate expected returns based on spefic factors.

A MULTIFACTOR MODEL uses macroeconomic, fundamental and (less so due to accuracy) statistical factors - with estimates of how sensitive a security is to changes in particular factors.

Question 13

Multi Factor Model Equation =

Answer 13

expected return above the risk free rate = the sensitivity, or factor loading (Bs), x expected value of the factor for the period.

First factor is often E(Rm-Rf), the expected market return.

Question 14

Fama and French Model (+Carhart) =

Answer 14

Fama and French multifactor model: firm size, firm book value to market value ratio, return on the market portfolio - risk free rate.

Carhart adds a fourth facto - price momentum using prior period returns.

Question 15

Single factor/index model =

Answer 15

expected excess return based on on factor exposure to the market return, factor weight/sensitivity “BETA i”

Question 16

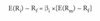
Market Model - to estimate a security’s alpha and beta =

Answer 16

market model is a simplified form of a single index model.

intercept ALPHAi and slope coefficient BETAi are estimated from historical return data.

ALPHA is Rf(1-BETAi)

Expected return is ALPHAi +BETAi(E(Rm))

ei is a deviation from this expected return

factor sensitivity/beta for asset i measures how sensitive its returns are to the return of the overall market portfolio

Question 17

BETA =

Answer 17

the sensitivity of an asset’s return to the return of the market index (in the market model context)

standardized measure of the covariance of the asset’s return with market return

SEE FRONT OF CARD FOR STARTING FORMULA, KNOW HOW TO CALCULATE BETA FROM THESE FORMULAS

Question 18

Graphing beta and the SECURITY CHARACTERISTIC LINE =

Answer 18

Extra context: we would calculate beta by regressing asset returns and market returns against each other to get a line of best fit.

the slope of this line is the sensitivity of asset excess returns (dependent variable) to market excess returns (independent variable) = BETA

SECURITY CHARACTERISTIC LINE is this regression line, with slope COVim/VARIANCEm (the formula for beta)

Question 19

CAPM Eqn and the SML (security market line) =

Answer 19

excess return is a function of systematic risk (this is the only risk we are compensated for) - so we can plot the two against each other –> these equations rearrange to the simple CAPM eqn (E[R] = Rf + B(Rmkt - Rf)

Question 20

Comparing the CML and SML =

Question 21

CAPM - definition =

Answer 21

an equilibrium model that predicts the expected return on a stock given

• the expected return on the market
• stock’s beta coefficient
• risk free rate

Question 22

Using CAPM to estimate the cost of equity =

Answer 22

we can use the CAPM model to find the expected return for a security, which is also the REQUIRED RATE OF RETURN FROM INVESTORS aka THE COST OF EQUITY

as an extension we could combine this with the cost of debt and a capital structure breakdown to get WACC for a firm.

Question 23

Valuations and plotting vs SML =

required return implied by beta risk vs analyst’s estimated return

Answer 23

A stock is OVERVALUED if the required return based on its BETA risk is GREATER than an analysts expected return for the stock. (vice versa for undervalued)

when a stock is OVERVALUED it plots below the SML line (which shows the E(R) based on B, or systematic risk)

ANY STOCK NOT PLOTTING ON THE SML LINE IS MISPRICED - an overvalued security needs to be cheaper so that the E(R) is compensating for the beta risk

Question 24

Sharpe Ratio =

Answer 24

excess returns per unit of total portfolio risk

this is a slope measure - of the CAL (Capital Allocation Line) for the portfolio

Note that the slope of the CML is the sharpe ratio for any portfolio on the CML line.

Question 25

M^{2 =}

Answer 25

produces the same portfolio rankings as the sharpe ratio but as a percentage

= (Rp - Rf)[SDm/SDp] - (Rm-Rf)

Question 26

Treynor Measure =

and Jensen’s Alpha

Answer 26

excess returns per unit of systematic risk, BETA.

(Rp-Rf)/B

Jensen’s alpha: percentage portfolio return above that of a portfolio(or security) with the same beta that lies on the SML

Question 27

When to use total risk/systematic risk measures =

And can we use them in practice?

Answer 27

whether to use measures based on total risk (sharpe, M²) depends if the fund bears the nonsystematic risk of a managers portfolio –> if a single manager is used then we should use the total risk measures.

Estimating the values needed to apply these models is difficult and is done with error.

The expected return on the market and thus the market risk premium may not be equal to the average historical value. Estimating betas is also done with error.