Picture/Symbol Cards

Question 1

Describe the resolution of vectors

• Formula for resolving vectors
• Two formulas for reconstructing resolved vectors

Answer 1

Question 2

Identify the two important trigonometric identities that link sine and cosine

Answer 2

Question 3

What is the pythagorean theorem?

Answer 3

r² = x² + y²

^{This only works on right angle triangles}

Question 4

It is important to memorize certain common values of trigonometric functions. List the sinθ, cosθ and tanθ values for the following angles (θ):

0°
30°
45°
60°
90°
180°

Answer 4

Question 5

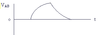
Recall the graph representing instantaneous velocity

Answer 5

Question 6

What is the formula used to determine average acceleration between two points in time?

Answer 6

Where v’ is final velocity and v is initial velocity.

Question 7

What is a uniformly accelerated motion and how can you measure total displacement of it?

Answer 7

Of the magnitude of forces acting on an object are constant, the magnitude of acceleration will be constant (resulting in unformly accelerated motion). The initial displacement, velocity and acceleration at any given time contribute to the overall displacement of the system.

displacement: x = x₀- x_f (due to initial displacement)

x = v₀t (displacement due to inital velocity at t)

x = ½at²(displacement due to acceleration at t)

Total displacement: x = x₀+ v₀t + ½at2

The translational motion is the motion of the centre of gravity of a system (ie object) through space, illustrated by the above equation

Question 8

List the three most important equations of kinematics (objects in motion with respect to space and time).

These must be memorized!

Answer 8

x = x₀ + v₀t + ½at²

v = v_o+ at

v² = v_o² + 2ax

Question 9

What is the law of gravitation? Provide the formula expressing this

Answer 9

The law of gravitation states that there is a force of attraction existing between any two bodies of masses m1 and m2, the force is proportional to the product of the masses and inversely proportional to the square of the distances between them.

F = K_G(m₁m₂)/(r²)

r: distance between the bodies, KG is the universal constant of gravitation (value depends on units)

Question 10

What is the equation for uniformly gravitationally accelerated motion?

Average velocity of free fall?

Answer 10

x = x_o + v_ot + ½gt²

v = gt

Question 11

How is the vertical component of a projectile motion calculated for:

initial speed

displacement at time t

Speed at any time t

Answer 11

Initial speed: V_oy = V_osinα

displacement at t: y = V_oy + ½gt²

speed at t: V_y = V_oy + gt

Question 12

How is the horizontal component of a projectile motion calculated for:

intiial speed?

displacement at any time t?

speed at any time t?

Answer 12

initial speed: V_ox = V_ocosα

displacement at t: x = v_oxt

speed at time t: V_x = V_ox (speed is constant due to negligable air friction)

Question 13

After calculation (or presentation) of the vertical and horizontal components of a projectile motion, how do you calculate:

magnitude of inital velocity?

Direction of motion?

Answer 13

Question 14

How can you calculate the horizontal distance from the origin of a projectile motion?

Answer 14

Question 15

Give the formula for the maximal frictional force

Answer 15

f_max = μN

Where μ is the coefficient of friction and N is the normal force to the surface on which the object rests (always perpendicular to surface).

Question 16

What is static friction and what is the formula which allows the coefficient of static friction (μ_s) to be calculated?

What is the coefficient of kinetic friction (μ_k)?

Answer 16

μ_s = tanα

where α is the angle at which the object first begins to move on an inclined plane as the angle is increased from 0 degrees to α degrees.

μ_{k <}μ_s

μ_kexists when surfaces are always in motion.

Question 17

Display the forces and motions acting on/resulting from an object on a sloped surface. Contrast this to an object on a level surface.

Answer 17

Question 18

Describe uniform circular motion and the formulas that can calculate acceleration and force.

(This applies to things like balls on strings, cars banking on turns and wall of an amusement park rotor)

Answer 18

Magnitude of velocity is constant, but direction is constantly changing (and therefore the velocity vector is continuously changing).

• The velocity is always tangent to the circle, creating an acceleration directed radially inward, called the centripetal acceleration a_c

a_c = v²/r (where r is radius of circle)

Centripetal force (F_c) = ma_c = mv²/r

Question 19

Give the formulas for:

circumference of a circle

area of a circle

Answer 19

circumference of a circle: 2πr

area of a circle: πr²

Question 20

For pully systems, give the formulas for:

acceleration of the objects (a)

tension on the string (T)

Answer 20

Note: T is always between the weight of mass m₁ and m₂

Question 21

What are two kinds of collisions that objects can have?

Give a formula for calculating the motion before and after a collision

Answer 21

• Elastic (objets rebound off each other, conservation of kinetic energy and momentum)
• Inelastic (Objects stick together, there is conservation of momentum, but not kinetic energy, which is lost as heat or sound)

m₁v_1i + m₂v_2i = m₁v_1f + m₂v_2f

If directions are not the same, then the each momentum must be resolved into x and y components as necessary.

Question 22

What is kinetic energy? How can it be calculated?

Answer 22

Kinetic energy (E_k) is the energy of motion which can produce work. It is proportional to the mass of the object and its velocity

E_k = ½(mv²)

Question 23

What is potential energy? How is it calculated?

Answer 23

Potential energy (E_p) is accumulated by the system that contained it. It varies with the configuration of the system (ie distances varying = interactions between particles vary).

The variation of the potential energy is equal to the work performed by the interior forces caused by the interaction between the particles of the system.

Question 24

Give formulas for the following examples of potential energy (E_p)

• Electric potential
• Universal attraction E_p
• Gravitational force E_p
• Elastic force E_p

Answer 24

Electrical potential: E_p = kq₁q₂/r

(q = point charge, r = distance between each)

**Universal attraction: **E_p = Gm₁m₂/r

**Gravitational force: **E_p = mgh

(h = height)

**Elastic force: **E_p = kx²/2

(k = spring constant, x = displacement)

Question 25

What is the definition of mechanical energy? Give the formula and the theorem of mechanical energy.

Answer 25

The mechanical energy (E_T) of a system is equal to the sum of its kinetic energy and its potential energy

E_T = E_k + E_p

Theorem of mechanical energy

The variation of teh mechanical energy of a system is equal to the work of exterior forces acting on the system. Consequentialy, an isolated system keeps a constant mechanical energy. The kinetic energy and teh potential energy may vary separately, but their sum remains constant. This makes conservation of energy a very simple way to solve many different types of physics problems.

Question 26

Why is friction not a conservative force? Give a couple examples of such a force.

Answer 26

It disobeys all three rules of a conservative force

1. After a round trip, the kinetic energy of a particle on which a force acts, must return to its initial value.

2. After a round trip, the work done on a particle by a force must be zero

3. The work done by the force on a particle depends on the initial and final positions of the particle and not on the path taken

• The force, Fs = -kx (Hooke’s law) of an ideal spring on a frictionless surface is a conservative force.
• Gravity is a conservative foce. If you throw a ball vertically upward, it will return with the same kinetic energy it had when it left your hand (neglecting air resistance).

Question 27

Give the formula for change in pressure with varying depth below the surface

Answer 27

ΔP = pgΔh

where h = depth below surface

p = density

Question 28

Give the formula for buoyant force (F_b). What predicts if an object will float?

Answer 28

F_b= Vph = mg

Where p = density of the displaced fluid

An object will float if it displaces at most its own weight

Question 29

Give the formula for the rate (R) of streamline flow for a fluid in motion.

Give the continuity equation

Answer 29

R = (volume past a point)/time = Avt/t = Av

Where volume equals Av (cross sectional area x length) = (A)(vt) = Avt

Length = distance = velocity x time = vt

Cross section of tube can be calculated by: area of circle (πr^2)

Continuity equation for incompressible fluid:

A₁V₁ = A₂V₂ = constant

Continuity equation for compressible fluid:

p₁A₁V₁ = p₂A₂V₂ = constant

Question 30

Give Bernoulli’s equation for the motion of fluid and commonly encountered consequences of the equation

Answer 30

P + pgh + ½pv² = constant

it follows: P₁ + pgh₁ + ½pv₁² = P₂ + pgh₂ + ½pv₂²

Where subscripts 1 and 2 indicate different points in the flow.

A commonly encountered consequence of Bernoulli’s equation is that where the height is relatively constant and the velocity of a fluid is high, the pressure is low and vice-versa

Question 31

Show a schema for shear modulus (S) on a solid object

Answer 31

Question 32

What happens when objects gain or lost heat?

Answer 32

Undergo expansion or contraction (linearly or by area or volume)

Question 33

What is a transverse wave?

Answer 33

A wave where the direction of vibrations is perpendicular to the direction of propagation of the wave (eg. light or oscillating string under tension).

Question 34

What is a longitudinal wave?

Answer 34

A wave where the direction of vibration is in the same direction as teh propagation of the wave (eg. sound)

Longitudinal waves are characterized by condensations (regions of crowiding of particles) and rarefactions (regions where particles are far apart) along the wave, in the medium.

Question 35

Recount schematics of maximally constructive and destructive wave interferences.

Answer 35

Question 36

Recount Thomas Young’s double slit experiment and what it revealed about wave interference.

Answer 36

Particle/wave duality was demonstrated with photons filtering through slits in screens. A light and dark banding pattern was observed on a screen due to constructive/destructive wave interference

Question 37

What are nodes in periodic/wave motion?

Answer 37

Nodes are points where there is no particle displacement, which are similar to points of maximal destructive interference.

Nodes occur at fixed end points (points that cannot vibrate)

Antinodes are points that undergo maximal displacement and are similar to points of maximal constructive interference. Antinodes occur at open or free end point.

Question 38

What is Hooke’s law in periodic motion? How can work be determined with this law?

Answer 38

• Particles that are undergoing displacement when a wave passes through a medium undergo motion called simple harmoni cmotion (SHM) and are acted upon by a force described by Hooke’s law.

Simple harmonic motion is causesd by an inconstant force (called a restoring force) and as a result has an inconstant acceleration. The force is proportional to the displacement (distance from the quilibrium point) but opposite in direction.

Hooke’s law: F = -kx

Where k = spring constat, x = displacement from equilibrium

Work (W) can be determined by W = ½kx²

Question 39

Recall a visual representaiton of Hooke’s law with an object exhibiting simple harmonic motion.

Answer 39

F: force, k: spring constant, x: displacement

Question 40

Give 6 important features of Hooke’s law for simple harmonic motion

Answer 40

1. Force and acceleration are always in the same direction
2. Force and acceleration are always in the opposite direction of teh displacement (accounting for the (-) sign in the equation for force)
3. Force and acceleration have their maximal value at +A and -A, they are zero at the equilibrium point
4. Velcity direction has no constant relation to displacement and acceleration
5. Velocity is maximum at equilibrium and zero at A and -A
6. The period (T) can be calculated from the mass (m) of an oscillating particle with T = 2π(m/k)^½

^{where k is the spring constant, the frequency f is simply 1/T}

Question 41

How can the period (T) of a periodic motion be calculated with the mass of the oscillating particle?

Answer 41

k: spring constant

Question 42

Give the equation for the intensity of sound

Answer 42

I = f²A²

f: frequency

A = Amplitude

Question 43

How do you calculate the decibels of a sound? How do calculate the change in sound level or volume (ΔV)

Answer 43

dB = 10log₁₀(I/I₀)

dB: sound level

I = the intensity at a given level (f₂A₂)

I₀: the threshold intensity

ΔV= 10log(I_new/I_old)

Question 44

How do you calculate sound intensity?

Answer 44

I = (x)I₀ = (10^x)I₀

Thus dB = 10log₁₀(10^xI₀/I₀)

dB = 10log₁₀(10⁷)

dB = 70log₁₀10

dB = 70

Question 45

How is the absolute value of the difference of sound frequencies calculated? What does this ‘absolute value of the difference of sound frequencies’ mean for complex sound?

Answer 45

With beats, the number of beats per second is the absolute value of the difference of the frequencies

|f₁ - f₂|

Hence the new frequency heard includes the original frequencies and the absolute difference between them

Question 46

Give the equation for doppler effect on frequency

Answer 46

f₀ = f_s(V ± v₀)/(V ± v_s)

V = speed of the wave

v = speed of the observer (o) or source (s)

Choose the sign such that the frequency varies consistently with the relative motion of the source and the obserer:

Distance increasing: -v_o and +v_s

Distance decreasing: +v_o and -v_s

Question 47

What is Coulomb’s law and what is it used to calculate?

Answer 47

The force that is generated by two repelling or attracting charges

k: coulomb’s constant
r: distance between the charges

Question 48

Give the equation for determining the vector, electric field (E)

Answer 48

E = F/q = kQ/r²

Where E and F are vectors,

Q: the charge generating the field

q: the charge placed in the field

Question 49

What happens if an electric potential is applied between two plates in a vacuum, and an electron is introduced?

Answer 49

The electron will experience an attractive force to the positive plate. The force will cause the electron to accelerate towards the positive plate in a straight line. It suffers no collisions because the area between the plates is in vacuo. This effect is used in thermoionic valves.

By varying the potential applied to the plates, the angle of deflection can be controlled (depicted in picture)

Question 50

Give the formula for the potential energy of a charged particle

Answer 50

E_p = work = Fr = (qE)r = kQq/r

Q: the charge setting up field

q: the object charge brought in to a distance r

THe potential energy of a charged particle in a field equals the work done on that object to bring it from infinity to a distance (r) from the charge setting up the electric field

When a positive q moves against E, its E_p increases. Work needs to be done to bring two positive or two negative charges together.

Question 51

Describe the physics of the following situation with equipotential lines

Answer 51

1. V₁ and V₂ are two potentials perpendicualar to the electric field (E) and the force (F) V₂-V₁ is the potential difference
2. Charge (q) moved from A (V₁ = .5) to B (V₂ = 1)
3. This shows that work has been done on it
   
   1. W = q(V₂ - V₁) = q(PD)
4. Charge q moving from A to C has no work done on it because this is along an equipotential surface (V = .5) and the non-zero component of force is perpendicualr to it
5. The lines of F are along the lines of E

Question 52

What is the potential difference (PD)?

Answer 52

The difference in V between two points, or it is the work per unit positive charge done by electric forces moving a small test charge from the point of higher potnetial to the point of lower potential:

PD = V_a - V_b = volts = work/charge

work = q(V_a - V_b) = q(PD)

Question 53

Describe magnetic induction, with two conductors a distance apart.

What are the forces?

Answer 53

Two straight conductors (Eg. copper wire) with electric current at intensity I and I’ in the same direction, are acted upon by an attractive force proportional to the product of the intensities and inversely proportional to the distance between the two conductors. It can be demonstrated that when the electric current in one of the conductors disappears, the force also disappears. Therefore the force is due to the motion of the electric charges in both conductors.

1. A moving charge produces a magnetic induction
2. A magnetic induction exerts a force on any nearby moving charge

Question 54

Recall the complete electromagnetic spectrum

Answer 54

Question 55

What is the symbol of an ammeter and what is it?

Answer 55

Ammetres measure the flow of current

Question 56

What are the two types of resistance?

Answer 56

Constant (normal) resistance

Variable resistance (ie. in a rheostat)

Question 57

How is equivalent resistance calculated in a:

Series circuit?

Parallel circuit?

Answer 57

Series: R_eq = R₁ + R₂ + R₃ etc…

Parallel: 1/R_eq= 1/R₁ +1/R₂ + 1/R₃ etc…

Question 58

What is the symbol for an emf source?

Answer 58

Question 59

How can you calculate the terminal voltage/termial potential of an emf?

Answer 59

V_t = V - Ir = IR_t

I, R_t = totals for the circuit

V = maximal voltage output of the emf source

Question 60

What are two Kichoff’s laws?

Answer 60

Kirchoff’s law I: When different currents arrive at a point, the sum of current equals zero.

Σi = 0 at junction

Kirchoff’s law II: The sum of voltage changes in one continuous loop of a circuit is zero. A single loop circuit is simple since the current is the same in all parts of the loop, hence the loop theorem is applied only once.

Kirchoff’s Law II: ΣΔV = 0 in a loop

Question 61

Recall the components of parallel plate capacitors and ceramic capacitors

Answer 61

Question 62

Give three important equations for capacitators

Answer 62

C = Q/V (V = potential between plates)

V = Ed (E = electric field strength, d = distance between plates)

C = ε_oA/d

(A = surface area of plates, d = distance between plates) or:

C = (k)εoA/d where k is the dielectric constant for a given material (not always needed)

Question 63

How is equivalent capacitance (C_eq) for capacitors calculated in circuit series and in parallel?

Answer 63

Series: 1/C_eq = 1/C₁ + 1/C₂ etc.

Parallel: Ceq = C₁ + C₂ etc.

Question 64

What do dielectric substances do in capacitors?

Answer 64

The dielectric substances set up an opposing electric field to that of the capacitor, which decreases the net electric field and allows the capacitance of the capacitor to increase (C = Q/Ed). The molecules of the dielectric are dipoles which line up in the electric field.

Question 65

What is the difference between DC and AC current? How do you calculate power output for each?

How do you calculate the rms values of AC circuits?

Answer 65

Direct current circuits contain a continuous current.

P = I²R = IV

Alternating current circuits pulsate; so we can only look at average power output

P_av = (I_ms)² = (I_ms)(V_ms)

Ims = I_maxI/2^1/2 amd V_ms= V_maxI2^1/2

Question 66

Recall concave and convex mirrors. Define the following on them:

• Radius of curvature (r),
• Centre of curvature (C)
• Focal point (F)
• Vertex (centre of mirror)
• axis (line through C and V)
• focal length (distance from F to V)
• image distance (i) (distance from V to image along axis)
• Object distance (o) (distance from V to object along axis)
• Linear aperture (AB) (cord connecting the ends of the mirror, the larger the aperture, the better the resolution

Answer 66

Capital letters refer to a point (or position) and small case letters refer to a distance

Question 67

Give snell’s law for refracted light

Answer 67

Constants don’t need to be memorized.

θ₁ = angle to the normal of incident light

θ₂ = angle to the normal of refracted light

Question 68

Explain this figure of refraction

Answer 68

With Snell’s law!

Question 69

Why does an object appear larger than it actually is under water when looking at it from above the surface?

Answer 69

Refraction

apparent depth/actual depth = n₂/n₁

n₂ is the density of the medium of the observer (assumedly air)

n₁ is the density of the medium of the object

Question 70

Describe converging (convex) and diverging (concave) lenses (recall schematic of both)

Answer 70

Question 71

Give the lens equations (same as mirror equation)

and lens maker’s equation

Answer 71

1/o + 1/i = 1/f

diopters = D = 1/f (lens maker’s equation)

Question 72

How can you calculate refractive power of lenses in series?

How can magnification be determined for lenses in series?

Answer 72

By adding the diopters of the lenses together, which can then be converted into focal length.

D_T = D₁ + D₂ = 1/f_T

M = -1/o = M₁M₂

Question 73

What is nuclear binding energy (E_b)? How is it calculated (famous equation)?

Answer 73

The result of the relation between energy and mass changes associated with nuclear reactions

ΔE=Δmc²

m: grams
c: cm/sec

ΔE: energy released or absorbed

Δm: mass lost or gained, respectively

c = velocity of light

Question 74

Give the relationship between binding energy and mass number.

Also between atomic number (protons) and number of neutrons (and how this effects stability)

Answer 74

Question 75

Spontaneous radioactivity (emission of particles) is common. What are the common emitted particles? (5)

Answer 75

• α particle: ₂He⁴ (helium nucleus)
• β particle: _-1e⁰ (an electron)
• positron: ₊₁e⁰(same mass as e^-, but positive charge)
• γ ray: no mass, no charge, just electromagnetic energy
• Orbital electron capture, where the nucleus takes electrons from K shell and converts a proton to a neutron. If there is a flux of particles, such as neutrons (₀n¹), the nucleus can absorb these also

Question 76

What is the half life (T_1/2) of a radioactive atom? How is the half life related to k (decay constant)?

Answer 76

The time required for one half of the substance to disintegrate. The half life is related to k as follows:

T_1/2 = 0.693/k

Question 77

What is the maximum number of electrons in an orbital shell of an atom? (give formula)

Answer 77

N_electrons = 2n²

Question 78

Recall a schematic of energy levels (E_n) for each atomic orbital shell (measured in electron volts)

Answer 78

Question 79

Recall a schematic that displays step 1 and 2 of fluorescence (light absorption followed by light emission). Demonstrating changes in energy levels (E) that correspond to changes in the frequency of light (f)

Answer 79

Question 80

How can the total energy of the electrons in an atom by calculated?

Answer 80

E_total = E_emission (or E_ionization) + KE

Question 81

List the three steps of fluorescence.

Answer 81

1. Absorption of light
2. Spontaneous deactivation of vibrational levels to zero vibrational level for electronic state
3. Fluorescence with light emission (longer wavelenth than absorption)

Question 82

What is the formula for centripetal motion?

Answer 82

a_c = v²/r

Question 83

How can you determine the velocity of an object in circular motion if given the radius of the circle and the time it takes to get around it?

Answer 83

V = circumference/time

V = 2πR/T

Question 84

How can you determine power dissipated as heat in a resistor?

Answer 84

Power dissipated as heat in the resistor is given by the square of the current times the resistance

P = I²R

Question 85

Answer 85

3 A

Currents in parallel resistors are inversely proportional to their individual resistances because they have the same voltage drop across them (Ohm’s law). Since the 2 ohm resistor in the diagram has 2 A, the parallel 4 ohm resistor has 1 A through it. These currents add to 3 A as they combine to pass through the ogm resistor (Kirchhoff’s junction rule).

Question 86

For a given magnitude of B, a nucleus with a nonzero precession frequency will be which of the following:

Answer 86

Question 87

Answer 87

θ = θ’ and θ>α

Because the medium’s surfaces are parallel a perpendicular line drawn to the lower surface of the medium will be parallel to both of the perpendiculars shown in the figure. This means that the angle of incidence at the lower surface will also be α, as will the angle of reflection at the lower surface, and the beam reflecting from the lower surface of the medium will then be a mirror image of the incoming beam, so θ’ = θ. Further, because air’s index of refraction is about 1.0, Snell’s law would show that θ>α

Question 88

What are the three components of the law of hydrostatic equilibrium?

Answer 88

1. The pressure at two points separated vertically by height h are related by:

P₂ = P₁ + ρgh

2. The pressures at two points separated only horizontally are the same
3. And the pressure at a given point is the same in all directions

Question 89

How is the total energy of a mass on a spring calculated at any given moment?

Answer 89

ET = Ep + Ek

ET = ½kx² + ½mv²

Potential energy and kinetic energy are constantly being transformed into each other during frictionless simple harmonic motion.

Question 90

What is the formula for figuring out the intensity of a sound a certain radius away from the source?

Answer 90

I = I_o(r_o/r)²

In words, the intensity decreases as the radius increases (with an inverse square law).

Question 91

What is Snell’s law?

Answer 91

If a beam of light encounters a boundary, and if the beam is transmitted, the transmitted beam is refracted, or bent, according to:

n_i sinσ_i = n_r sinσ_r

Where n is the index of refraction (higher value indicates slower speed, V = c/n). σ is the angle of the beam, measured from the normal.

Question 92

A mass falls from 20 m to the ground. The mass is dropped from 10 m in a second trial. How does the speed of the mass at the end of the second trial compare to the end speed of the mass when starting from 20 m?

Answer 92

It is slower by a factor of √2

Equating the loss of potential energy (mgh) to gain of kinetic energy (½mv²), the ratio of speeds before hitting the ground is 10/20.

Taking the square root gives (½)^½, showing that the speed is slower by a factor of √2

Question 93

In a nearsighted individual, the image of a distant object is focused ____ the retina, requiring ____ lens correction.

Answer 93

The image of a distant object is focused in front of the retina, requiring divergent lens correction.

Question 94

Two converging lenses are in contact, if the focal lengths of each are 5 cm, what is the equivalent focal length of the combination?

Answer 94

1/f_T = 1/f₁ + 1/f₂

1/f_T = 1/5 + 1/5

f_T = 2.5

Question 95

Give the definition of a real image and a virtual image

Answer 95

In optics, a real image is an image which is located in the plane of convergence for the light rays that originate from a given object. If a screen is placed in the plane of a real image the image will generally become visible on the screen.

A virtual image is an optical image formed from the apparent divergence of light rays from a point, as opposed to an image formed from their actual divergence.

Question 96

Contrast a real and virtual image for lenses

Answer 96

Question 97

Contrast a real and virtual image for mirrors

Answer 97

Question 98

Which of the following shows the boiling point of an aqueous sodium chloride solution as a function of the percent sodium chloride in the solution by weight?

Answer 98

B

Molality does not increase linearly with the percent of solute in solution. The change in boiling point comes on gradually and increases as the saturation increases, making B the best choice.

Question 99

In the arrangment shown, a current flows from P to Q and has the ammeter A1 read 3.0 A. If each ammeter has negligible resistance, what is the reading on ammeter A2?

Answer 99

1. Total current = 6 A
2. Second series resistance: 1/RT = 1/2R + 1/R = 3/2R
   
   1. RT = 2R/3
3. V = IR
   
   1. V = (6)(2R/3)
   2. V = 4R
4. I = V/R
   
   1. I = 4R/R = 4

The answer is 4 A

Question 100

Memorize the following squares

11² =

12² =

13² =

14² =

15² =

Answer 100

11² = 121

12² = 144

13² = 169

14² = 196

15² = 225

Question 101

A = B^½

If B increases by 44%, by what % will A increase by?

Answer 101

This is the same as saying B(1.44)^½

We know that the square root of 1.44 is 1.2 (12² = 144), therefore A has increased by 20%!

Question 102

What is:

2^½ =

3^½ =

Give the answers in decimals and the simplest fractions possible.

Answer 102

2^½ = 1.4 = 7/5

3^½ = 1.7 = 17/10

Question 103

Batman (70 kg) jumps off a bridge and lands on a sticky surface 10 m below him. What is his velocity just before he lands?

Answer 103

You need to figure out potential energy (mgh). Potential energy is transformed into kinetic energy

E_p = ½mv²

therefore

(70)(10)(10) = ½mv²

v = 14.14

Note that mass cancels out and therefore is not relevant in this case!

Question 104

Give the formulas for work and force on a spring

Answer 104

W = ½kx²

F = -kx (Hooke’s Law)

Question 105

What is the energy of an alpha particle (a helium nucleus) under a potential difference of 20 V?

Charge of an electron = 1.6 x 10^-19 C

Answer 105

The charge on the helium nucleus is caused by the loss of two electrons (He²⁺), each having the same charge.

Since it must have an equal but opposite charge to the sum of the charges of the two electrons, its charge = 1.6 x 10^-19 x 2 = 3.2 x 10^-19 C.

From E = qV

E = 3.2 x 10^-19 C x 20 V = 64 x 10^-19J = 6.4 x 10^-18 J

Question 106

Give the formula that allows you to calculate the energy stored in a capacitor

Answer 106

E = ½QV

England hails Queen Victoria

Question 107

How the frig do you compare the intensity level of two sounds?

Eg. How many times greater is the intensity level of sound B if sound B is 20 dB greater than the intensity level of sound A?

Answer 107

β: intensity level

β = 10log(I/I₀)

I: intensity of the sound
I₀: minimum intensity audible to human ear

eg. β_B - β_A = 10Log(I_B/I_A)

20 = 10Log(I_B/I_A)

Log(I_B/I_A) = 2

I_B/I_A = 10² = 100

Question 108

A square wave voltage signal is sent into a resistor-capacitor circuit as shown.

What will a plot of V_AB vs. time look like? Why?

Answer 108

• Voltage across capacitor is dependent on charge due to current inflow
  
  • Current inflow is limited by the resistor (I = V/R)
• The capacitor charges (increasing voltage between A and B) exponentially
• The capacitor discharges exponentially as well

To answer this question, you must consider how R changes as voltage changes, and how this will effect the overall terminal voltage.

Question 109

How can you determine the height change of a fluid in a cylindrical tank if something is placed into it?

Change of pressure?

Answer 109

Δh = V_object/A_tank

Where A_tank is πr²

ΔP = ρgΔh