Pharmacokinetics

Question 1

What is Euler’s number?

Answer 1

e = 2.718

This is a constant which describes exponential processes.

The variable increases or decreases at a rate that is proportional to it’s own magnitude.

Question 2

What can Euler’s number be used to describe?

Answer 2

• compound interest
• probability theory
• radioactive decay
• redistribution and metabolism of drugs
• properties of biological APs
• charging and discharging of a capacitor
• bacterial growth

Question 3

What is a tear-away function?

Answer 3

A variable increase in magnitude of a quantity

Question 4

What is an asymptote?

Answer 4

WHen the curve gets ever closer to the axis but never meets it (eg radioactive decay or elimination of drug from the body).

Question 5

What is the shape of the end tidal N2 concentration against time during pre-oxygenation?

Answer 5

It is an exponential function.

To make the graphical representation easier, a natural logarithmic transformation applied to the variable that is plotted against time gives a straight line by compressing the concentration axis.

Question 6

What are natural logarithms to the base of?

Answer 6

To base 2.718, or base e, because they deal with naturally occuring processes.

Question 7

What happens if you plot N2% to the base e against time?

Answer 7

You get a straight line.

Question 8

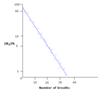
How can you tell the difference between an exponential graph and rectangular hyperbola?

Answer 8

• both asymptote the x-axis
• exponential curve meets the y-axis
• hyperbolic curve asymptotes the y-axis
• rectangular hyperbola is a section of a cone
• exponential function models naturally occurring processes

Question 9

What does the graph of current vs time look like when charging a capacitor?

Answer 9

It looks like a drug elimination curve, because as charging proceeds less electrons are required to attempt to complete the charge and the current therefore falls

The charge vs time and the voltage vs time graphs would resemble wash-in curves.

Question 10

What do natural exponential processes need to produce straight line graphs?

Answer 10

They need natural logarithmic transforms

Question 11

What are the 3 constants that an exponential function can be described by?

Answer 11

• rate constant, k
• time constant τ (tau)
• half-life (t_1/2)

Question 12

What does the rate constant, k, describe in a decreasing exponential function?

Answer 12

The relationship between the rate of decrease and the magnitude of the variable.

In effect, mathematically, k is the ratio of the slope of the graph to it’s height.

You can work out the slope at any point and will find that the relationship of the slope to the height is constant.

Question 13

What are the units of the rate constant, k?

Answer 13

They’re the units of slope/units of height

ie m.sec-1/m or sec-1

In exponential processes that occur over time, the units of k are always sec-1.

Question 14

What is tau (τ), the time constant?

Answer 14

Can be described 4 ways:

• the time it would have taken for a negative exponential process to complete, were the initial rate of change to be maintained
• the time taken for the value of an exponential to fall to 37% of it’s previous value
• the time taken for the value of an exponential function change by a factor e¹
• the reciprocal of the rate constant

Question 15

How many time constants will an exponential process be complete after?

Answer 15

3 (94.9% complete at this point)

Question 16

What is the half-life?

Answer 16

The time required for the magnitude of the variable to fall to one half of it’s original value.

It must always be shorter time than that required to fall to 37% (the half life is always less than the τ )

Question 17

What is the relationship between the constants in a decreasing exponential function (pharmacokinetics)?

Answer 17

τ = 1/k

k = 1/τ

t½ = τ x 0.693

Question 18

What are the units of the rate constant?

Answer 18

Units of rate (eg per second)

Question 19

What is drug clearance?

Answer 19

The volume of plasma that is cleared of drug in unit time

Question 20

What are the units of drug clearance?

Answer 20

ml/kg/min and litres/min

Question 21

How is drug clearance related to τ?

Answer 21

It is volume of distribution divided by τ

Question 22

What is the volume of distribution?

Answer 22

A mathematical concept where a drug is evenly distributed through a hypothetical compartment.

When a drug does is delivered to a patient it results in a concentraion of that drug within the body. If it’s evenly distributed you get a virtual volume for that compartment (Vd) and a drug concentration in this volume.

Question 23

How are the different rate constant for the passage of drugs into the outside (ie eliminated) labelled?

Answer 23

o is outside and the numbers refer to the compartment

eg k_1o refers to the rate constant for passage of the drug from compartment 1 to the outside, ie elimination

Question 24

If you gave a theoretical patient 100mg of propofol, and their initial Vd was 10L, what would the concentration of each ml be?

Answer 24

It would be 10mg/L or 10mcg/ml

Question 25

What is the 3 compartment model of pharmacokinetics?

Answer 25

Drugs that follow this model include propofol and fentanyl.

These drugs often have an initial Vd that’s small, representing their initial dispersal in the plasma. This initial volume is the central compartment. and then they have a very large Vd at steady state (Vdss) when they’ve redistributed throughout all of the body tissues.

Question 26

What is clearance?

Answer 26

The virtual flow of the volume of distribution.

When a drug is cleared from the body by passage in the blood through an organ, usually the liver or kidney, the volume that is completely cleared is the clearance.

Can be thought of as:

• the flow of the mass of drug
• the flow of the volume of distribution

Question 27

What is the relationship between Vd and clearance?

Answer 27

If your clearance is 5L/min - the concentration in the compartment won’t fall by half in this minute because the elimination of drug is exponential, so the mass of drug eliminated per unit time is always reducing.

Cl = Vd / τ

Cl = k x Vd

Question 28

What is the initial distribution of propofol?

Answer 28

Schnider - 4.27L

Marsh - 15.9 L

(large initial Vd)

Question 29

Can you calculate the volume of distribution if the half life and steady state drug concentration are known?

Answer 29

Yes, you do not need to know t_1/2 for this method and do need to know Cl