Periodic Motion, Waves, and Sound

Question 1

simple harmonic motion def

Answer 1

• a particle/mass oscillates about an equilb position and is subject to a linear restoring force
• springs and pendulums
• type of periodic motoin where freq and ampitude don’t change
• energy is conserved E= K+U

Question 2

hooke’s law = ?

Answer 2

F= -kx

• negative sign means always restoring towards equilib position
• mag of Force prop to mag of displacement from equilib position
• k= spring constant (N/m) or (kg/s²)=measure of stiffness (bigger k means stiffer spring means greater mag. of restoring force).

Question 3

angular freq for a spring = ?

Answer 3

w=2πf=√k/m

• w= rad/s
• note freq doesn’t depend on x, but does tell us that the stiffer the spring (bigger k) or smaller the mass, the faster the spring will oscillate

Question 4

relate frequency and period for springs and pendulums

HINT: waver, wack ‘em, wiggle

Answer 4

f=1/T (cycles/sec)

T=period=1/f=(sec/cycle)

w=2πf so,

2π/T=w=2πf=v/r=√k/m=√g/l

• w=2πf always true
• w=v/r uniform cicular motion (waver)
• w=√k/m springs (wack ‘em)
• w=√g/l pendulums (wiggle)

Question 5

potential energy of a spring = ?

Answer 5

U= ½ kx²

(elastic potential energy)

think PE= force (kx) * distance (x) –> 1/2 kx²

Question 6

total mechanical energy of a spring = ?

Answer 6

E= K + U

E= ½mv² + ½kx²

E=½mv_max²+ 0

E=½kx_max² + 0

**Therefore use E=½kx_max² **

(b/c typ easier to find x_max when v=0 instead of finding v_max)

Question 7

Two identical springs (i.e. same values for m and k) are oscillating in simple harmonic motion on a frictionless surface. It is observed that that the maximum speed of one spring is different than the maximum speed of the other.

A) What is different about the two spring systems?

B) Which spring is oscillating with a greater frequency?

Answer 7

A) diff in max speed means max amplitude isn’t the same therefore energy is not the same

B) both same freq b/c w=√k/m

• NOTE: energy questions are DIFFERENT than freq. questions
  
  • energy deals w/ max speed/amplitude
  • freq deals w/ wavr, wackem, wiggle

Question 8

springs in series

Answer 8

k_eff= k₁ + k₂

F_eff=2kx

(springs in parallel like resistors in parallel but never seen tested before: 1/k_eq=1/k₁ + 1/k₂)

Question 9

pendulums = ?

Answer 9

F= -mgsinø

• where ø is angle b/w pendulum arm and the verticle
• gravity is the restoring force

Question 10

anguluar freq pendulum = ?

Answer 10

w=2πf= √g/l

• only gravity and length of pendulum contribute to freq. Mass and ø don’t matter, therefore two pendulums that are the same length will have the same freq ie pendulum pulled back at bigger angle will have to travel faster to complete cycle in same period

Question 11

what are the two ways to change w of a pendulum?

Answer 11

• increase w by making gravity bigger
• decrease w by making l bigger (will take longer time so w will decrease)

Question 12

potential energy of a pendulum = ?

Answer 12

U=mgh

again, conservation of energy w/ pendulums so

E=K+U

Question 13

You own a clock that keeps time by the swinging motion of a simple pendulum. If you transported the clock from the Earth to the moon, would the clock run slower, faster, or the same as it did on Earth?

Answer 13

Slower.

w=√g/l as go from earth to moon g decreases, so w decreases, and since w=2π/T, T increases therefore period is longer so clock is running slower

Question 14

A 9mm bullet (8.0 g) fired from a gun w/ a speed of 300 m/s lodges into a stationary wooden block (2.0 kg) suspended from the ceiling via a massless cord, length L. The collision causes block to behave as a pendulum.

• If the oscillation frequency of the block alone is f, what is the oscillation frequency of the bullet and block together?
• If the length was doubled to 2L, by what factor would the maximum height reached by the block change?

Answer 14

• w=√g/l neight of which are changing so freq stays the same, f.
• max height= energy question=got energy from bullet but changing L doesn’t effect energy therefore there would be no change in energy (making string longer wouldn’t affect energy it gains from the bullet)

Question 15

• What direction do the particles and wave travel for transverse waves?
• What are some examples of transverse waves?

Answer 15

• particles move up and down, perpendicullarly to the direction of travel of the wave (ie. the direction of energy transfer)
• light, electromagnetic, standing wave

Question 16

• What direction do the particles and wave travel for longitudinal waves?
• what are examples of longitudinal waves?

Answer 16

• the particles oscillate parallel to the direction of motion of the wave (ie. the direction of energy transfer)
• sound (major), pressure, earth quakes

Question 17

speed of a wave = ?

Answer 17

v= fλ

Question 18

wave number, k = ?

Answer 18

k= 2π/λ

(therefore v=fλ =w/k)

Question 19

when waves are in phase they have = ?

what will the difference in path length difference equal?

Answer 19

constructive interference. meaning their amplitudes add together and resultant wave has a great amplitude

the difference in path lengths of the wave, L₂-L₁= nλ

where n=0,1,2,3 etc.

Question 20

when waves are out of phase they have.. ?

what will the difference in path length difference equal?

Answer 20

destructive interference. The resultant wave’s amplitude is the difference b/w the amplitudes

the path length difference, L₂-L₁= nλ/2

where n=odd integer ie. λ/2, 3λ/2, 5λ/2

Question 21

properties of standing waves

Answer 21

• nodes= points along wave that remain at rest
• antinodes= points along wave that fluctuate b/w max and min amplitudes

Question 22

definition of mechanical wave

Answer 22

a traveling disturbance through matter that transfers energy, but not mass, from one point to another

• can’t go through a vacuum b/c nothing to push/disturb)
• includes longitudinal, transverse, and surface waves (surface= move in a cirlce ie mix of other 2)

Question 23

two trends to know:

• how does the speed of a mech wave change when go from solid to liquid to gas?
• how about when within media of same phase?

Answer 23

• decreases. v_{mech wv}= s>l>g
• v b/w media of same phase is inverse to denisty ie v_helium > v_air because helium less dense than air
• v hot objects > v cold objects

Question 24

what does the speed of a mech wave depend on?

Answer 24

• v_mech= √elasticity constant of medium (ie. Bulk modulus)/ density of medium

therefore, speed of wave is greatest in solids b/c they have biggest bulk modulus (elasticity constant)

Question 25

what is the definition of an electromagnetic wave?

Answer 25

EM waves transfer energy from one point to another w/o needing oscillation of particles. Oscillating electric and magnetic fields is how EM waves propogate.

therefore, EM waves CAN travel through a vacuum

Question 26

• how does the speed of an EM wave change when go from solid to liquid to gas?
• what factors influence the speed of EM waves?

Answer 26

• increases. opposite of mech waves. v_{EM wv}= s<l>
  </l><li>more atoms a wave has to go through the slower it is</li>

</l>

Question 27

speed of an EM wave = ?

Answer 27

v=c/n

c=3x10⁸ m/s

n=index of refraction, which is roughly prop to mass density

Question 28

Intensity of wave = ?

Answer 28

I=P/A (W/m²)

IPA

Question 29

what is the intensity of an EM wave proportional to?

what is the intensity of a mech wave proportional to? inversly proportional to?

Answer 29

• I of an EM wave is proportional to (E_field)² (b/c I=P/A and P=energy/time)
• I of a mech wave is proportional to (amp)² (E=1/2 kx_max²)
• I of a mech wave is inversely proportional to the (distance from the source)² ie. I=P/4πr²

Question 30

if you increase the frequency of a wave but keep everything else the same will the speed of the wave increase?

Answer 30

No. The only way to change the speed of a mech wave is to change the medium- if don’t change medium speed will not change. Therefore if increase the f, the wavelength will just decrease and v will remain the same.

Question 31

fill out this table for sound, light, water, and “stadium” waves

Answer 31

Question 32

1. what is the definition of a coherent source?
2. what is an example of a corherent source?
3. what are examples of non-coherent sources?

Answer 32

1. two coherent sources are necessary to product constructive or destructive interference b/c they emit waves that mantain a constant phase relation, ie as time passes, waves would not sift phase relationship
2. lasers (therefore if laser mentioned, think strong interference patterns)
3. incandescent light bulbs or florescent lamps are incoherent sources

Question 33

fill in this table for EM and mech waves at the interface b/w two media (boundary) when incident wave is going from air into water:

Answer 33

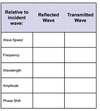
“higher=half” going into higher medium gives 1/2 phase shift

NOTE: E_{incident wv}= E_{reflected wv} + E_{transmitted wv}

Question 34

the speed of sound in at at 0˚C is 331 m/s. How does the speed change if it enters a medium of air at 20˚C?

Answer 34

PV=nRT since P, n, and R constant

V is prop. to T

Therefore, will be expansion of air as it heats up,

leading to LOWER density aka HIGHER speed

v_hot> v_cold

Question 35

why can dogs hear lower intensity sounds than humans?

Answer 35

b/c P_{at ear}=I_{at your location}/A_{ear canal}

since dogs have a larger ear canal, so can capture more of sound

(infrasonic waves<audilble>
</audilble>

Question 36

sound level = ?

Answer 36

B= 10 log (I/I_o)

where I_o= 1x10^-12 W/m²

• B is in decibles (dB)
• since is a reference intensity, B=0 doesn’t mean there is no sound
• intensities can add, but decibles cannot (b/c log scale)

Question 37

what is the key relationship that you can use instead of working with decible eqtn?

Answer 37

When B= 0, I= 10^-12 so Intensity x 10ⁿ : B + 10(n)

therefore any change in exponent from 10^-12 will result in that change x 10 in decible:

Question 38

what is the equation for stand waves for open pipes and strings tied at both ends?

Answer 38

λ=2L/n

when n ≠ 0

then since f= v/λ, f=nv/2L

Question 39

what is the equation for stand waves for closed pipes?

Answer 39

λ=4L/n

where n= an odd #

since f= v/λ, f= nv/4L

Question 40

what will tell you the number harmonic for strings tied at both ends?

pipes?

Answer 40

strings tied at both ends: # antinodes = # harmonic

pipes: # nodes= # harmonic

Question 41

what is the fundamental freq also known as?

what is the first overtone also known as?

Answer 41

first harmonic

second harmonic

Question 42

doppler effect = ?

when do you use the top signs and when do you use the bottom signs?

Answer 42

“top towards”

“bombs away” (bottoms away)

Question 43

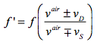
what are the three situations when the observed f is higher than the actual f?

Answer 43

• Source moving toward stationary observer: f^’ = f v/(v - v_s)
• Observer moving toward stationary source: f^’ = f (v + vd)/v
• Source and observer both moving toward each other: f^’ = f (v + v_d)/(v - v_s)

Question 44

what are the three situations when the observed freq is less than the actual freq?

Answer 44

• Source moving away from stationary observer: f’ = f v/(v + v_s)
• Observer moving away from stationary source: f’ = f (v - v_d)/v
• Source and observer both moving away from each other: f’ = f (v - v_d)/(v + v_s)

Question 45

when the source/detector are moving opposite one another ie. one moving towards the other moving away, what is the observed freq?

Answer 45

could be either higher or lower, need more info

Question 46

beat freq = ?

definition of beat freq?

Answer 46

f_beat= | f₁- f₂ |

beat freq is the fluctuation in volume resulting from two sound waves with nearly equal freqs resulting in a resultant wave with fluctuating amplitude.

Since the amplitude, not freq, of resultant wave varies, hear the sounds as variation in loudness, not pitch

Question 47

def pitch ?

Answer 47

our perception of the freq of sound= pitch

higher freq= higher pitch

Question 48

greater amplitude is associated with greater what?

Answer 48

Amplitude is correlated with the total energy of the system in periodic motion,

therefore Larger amplitude = greater energy = greater intensity

(The displacement is how far the wave vibrates / oscillates about its equilibrium (center) position)

Question 49

tense, light strings produce fast or slow transverse waves?

Answer 49

fast

Question 50

energy per photon of an EM wave = ?

Answer 50

E= hf = hc/λ

therefore the smaller the wavelength, the higher the freq, the greater the energy of a photon