Paradoxes and Common mistakes Flashcards
(2 cards)
Add
Simpson’s paradox,
Common mistakes (assumptions violated, etc)
Commercial misuse curretly and history
Famous mistakes in court, newspapers, etc.
Bayes vs. frequentist
ESP
gambling,
perception of probability/belief (97% chance of rain gambling ad)
Rare condition tests
Non intuitive outcomes
Simpson’s pardox
In probability and statistics, Simpson’s paradox (or the Yule–Simpson effect) is a paradox in which a trend that appears in different groups of data disappears when these groups are combined, and the reverse trend appears for the aggregate data. This result is often encountered in social-science and medical-science statistics, and is particularly confounding when frequency data are unduly given causal interpretations.Simpson’s Paradox disappears when causal relations are brought into consideration.
Kidney stone treatment
This is a real-life example from a medical study[12] comparing the success rates of two treatments for kidney stones.[13]
The table shows the success rates and numbers of treatments for treatments involving both small and large kidney stones, where Treatment A includes all open procedures and Treatment B is percutaneous nephrolithotomy:
Treatment A Treatment B
Small Stones Group 1
93% (81/87) Group 2
87% (234/270)
Large Stones Group 3
73% (192/263) Group 4
69% (55/80)
Both 78% (273/350) 83% (289/350)
The paradoxical conclusion is that treatment A is more effective when used on small stones, and also when used on large stones, yet treatment B is more effective when considering both sizes at the same time. In this example the “lurking” variable (or confounding variable) of the stone size was not previously known to be important until its effects were included.
Which treatment is considered better is determined by an inequality between two ratios (successes/total). The reversal of the inequality between the ratios, which creates Simpson’s paradox, happens because two effects occur together:
The sizes of the groups, which are combined when the lurking variable is ignored, are very different. Doctors tend to give the severe cases (large stones) the better treatment (A), and the milder cases (small stones) the inferior treatment (B). Therefore, the totals are dominated by groups 3 and 2, and not by the two much smaller groups 1 and 4.
The lurking variable has a large effect on the ratios, i.e. the success rate is more strongly influenced by the severity of the case than by the choice of treatment. Therefore, the group of patients with large stones using treatment A (group 3) does worse than the group with small stones, even if the latter used the inferior treatment B (group 2
One of the best known real life examples of Simpson’s paradox occurred when the University of California, Berkeley was sued for bias against women who had applied for admission to graduate schools there. The admission figures for the fall of 1973 showed that men applying were more likely than women to be admitted, and the difference was so large that it was unlikely to be due to chance.
Applicants Admitted
Men 8442– 44%
Women 4321— 35%
But when examining the individual departments, it appeared that no department was significantly biased against women. In fact, most departments had a “small but statistically significant bias in favor of women.
Department Men Women
Applicants Admitted Applicants Admitted
A 825 62% 108 82%
B 560 63% 25 68%
C 325 37% 593 34%
D 417 33% 375 35%
E 191 28% 393 24%
F 272 6% 341 7%
The research paper by Bickel, et al. concluded that women tended to apply to competitive departments with low rates of admission even among qualified applicants (such as in the English Department), whereas men tended to apply to less-competitive departments with high rates of admission among the qualified applicants (such as in engineering and chemistry). The conditions under which the admissions’ frequency data from specific departments constitute a proper defense against charges of discrimination are formulated in the book Causality by Pearl.
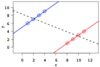
Example: Simpson’s paradox for continuous data: a positive trend appears for two separate groups (blue and red), a negative trend (black, dashed) appears when the data are combined.


