Oscillations and Waves

Question 1

Define and list examples of free oscillations

Answer 1

An oscillation whose frequency is the natural frequency of the oscillator.

e.g. guitar strings, tuning forks, pendulum

Question 2

Express the period of an oscillation in terms of both frequency and angular frequency

Answer 2

T = 1/f

ω = 2πf and f = ω/2π, so

T = 2π/ω

Question 3

Define

simple harmonic motion

Answer 3

The motion of an oscillator where its acceleration is directly proportional to its displacement from its equilibrium position and is directed towards that position.

a = -ω²x

Question 4

State the equations for displacement (x), velocity (v) and acceleration (a) if the oscillator starts from its equilibrium position

Answer 4

Taking x₀ as the maximum displacement,

x = x₀sinωt

v = x₀cosωt

a = -x₀ω²sinωt

Question 5

State the equations for displacement (x), velocity (v) and acceleration (a) if the oscillator starts from maximum displacement

Answer 5

Taking x₀ as the maximum displacement,

x = x₀cosωt

v = -x₀sinωt

a = -x₀ω²cosωt

Question 6

State the equation for maximum velocity and the equations for velocity

Answer 6

v₀ = x₀ω

v = v₀cosωt (starts from equilibrium position)

v = v₀sinωt (starts from max. displacement)

v = ±ω√(x₀² - x²)

Question 7

Ddescribe the interchange between kinetic and potential energy during simple harmonic motion

Answer 7

• Energy in s.h.m. is interchanged between kinetic energy and potential energy ONLY
• Provided the system is undamped, the total energy (k.e. + p.e.) remains constant
• k.e. is maximum at the equilibrium position and zero at maximum displacement
• p.e. is maximum at maximum displacement and zero at the equilibrium position

Question 8

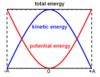
Derive equations for total energy, kinetic energy and potential energy in simple harmonic motion

Answer 8

substituting v = ±ω√(x₀² - x²) into ½mv²,

E_k = ½mω²(x₀² - x²)

when x = 0, E_t = E_k, ∴

E_t = ½mω²x₀²

E_p = E_t - E_k, ∴

E_p = ½mω²x²

Question 9

Define

damping

in s.h.m.

Answer 9

The continuous decrease in amplitude and energy of an oscillating system due to energy lost in overcoming resistive forces.

The amplitude of damped oscillations decreases exponentially.

Question 10

Explain the difference between light, critical and heavy damping.

Answer 10

• Light/under damping: The system oscillates about the equilibrium position with decreasing amplitude over a period of time.
• Critical damping: The system does not oscillate & damping is just adequate such that the system returns to its equilibrium position in the shortest possible time.
• Heavy/over damping: The damping is so great that the displaced object never oscillates but returns to its equilibrium position very very slowly.

Question 11

Define and list examples of forced oscillations

Answer 11

An oscillation caused by an external driving force whose frequency is equal to that of the driving force.

e.g. seats in transport

Question 12

Define

resonance

in s.h.m.

Answer 12

The forced motion of an oscillator characterised by maximum amplitude when the driving frequency matches the oscillator’s natural frequency.

A system absorbes maximum energy from a source when the source frequency is equal to the natural frequency of the system.

Question 13

List some circumstances in which resonance is useful and other circumstances in which resonance should be avoided.

Answer 13

Useful:

• microwaves causing water particles in food to oscillate
• wireless communication (broadcast tower amplifies signal)
• MRI

Not useful and should be damped:

• Buildings swaying during earthquakes
• People walking on a bridge that can oscillate

Question 14

Describe graphically how the amplitude of a forced oscillation changes with frequency near to the natural frequency of the system, and the effects of damping on resonance

Answer 14

• amplitude increases as natural frequency is approached
• amplitude and sharpness of response is decreased by damping
• damping slightly decreases the resonant frequency

Question 15

Explain the main principles behind the generation of ultrasound

Answer 15

• piezo-electic crystal such as quartz used as a transducer
• coated on opposite sides with silver to act as electrodes
• centres of +ve and -ve charge not coincident
• p.d. across crystal induces a strain and causes a change in shape
• alternating voltage applied across crystal causes oscillations
• the crystal is cut to optimum size (usually λ/2) so it vibrates at resonant frequency

Question 16

Explain the main principles behind the detection of ultrasound

Answer 16

• the transducer that generates ultrasound also detects ultrasound
• after sending a pulse, oscillation is damped by damping material so the crystal is not vibrating when the reflection is received
• the pressure variations of the ultrasonic wave alter the +ve and -ve ions within the crystal
• this induces a varying e.m.f. across the crystal that induces opposite charges on the silver electrodes
• the p.d. across the electrodes can be processed

Question 17

Explain the main principles behind the use of ultrasound to obtain diagnostic information about internal structures

Answer 17

• pulse of ultrasound is reflected at boundary
• the reflection is received by the transducer
• signal is processed and displayed
• time between transmission and receipt of pulse gives depth of boundary
• reflected intensity gives information as to the nature of the boundary

Question 18

Define

specific acoustic impedance

Answer 18

The product of the density of a substance and the speed of sound in that substance.

Z = ρc (kg m^-2 s^-1)

Question 19

Define

intensity reflection coefficient

Answer 19

I_R/I = (Z₂ - Z₁)² / (Z₂ + Z₁)²

This indicates the fraction of the intensity of the beam that is reflected.

Question 20

State the equation for the attenuation of ultrasound in matter

Answer 20

I = I₀e^–μx

where I is the transmitted intensity, I₀ is the incident intensity, μ is the absorption coefficient and x is the distance through the medium that the unltrasound travels.