Oscillations Flashcards
Considering a spring oscillating, give the definitions of the following: Displacement, Amplitude ,Period and Frequency
Displacement - distance from the equilibrium position
Amplitude - maximum displacement
Period - time taken for a complete oscillation
Frequency - number of oscillations per second
State equation relating angular frequency (scalar ) and time period
⍵ = 2π/T
Where ⍵ = angular frequency, T = time period
What are the conditions for simple harmonic motion
- acceleration is directly proportional to the displacement and is in the opposite direction
- must be directed towards equilibrium
( a=-⍵²x)
Give 2 examples of systems which undergo simple harmonic motion
pendulums and mass-spring systems
Describe an experiment to investigate simple harmonic motion using a data logger
- Attach mass to the end of a spring which is being held up by a clamp and place a position sensor under the mass (this should be connected to a computer/data logger)
- Lift mass slightly and and release -this will cause oscillation with simple harmonic motion.
- To ensure experiment is repeatable place a ruler behind the spring to measure how far you raise the mass
- Position sensor will measure displacement of mass over time which can then be used to generate a displacement-time graph
- From graph you can measure the time period of the osccilation and the amplitude
-to lower percentage error in measurements you can use a larger spring as it causes a larger amplitude of osccilations
What is 𝑥 as a function of t and ⍵?
𝑥 = Acos⍵t or 𝑥 = Asin⍵t (where A is amplitude)
Demonstrate how you would derive the equation for simple harmonic motion from 𝑥 = Asin⍵t or 𝑥 = Acos⍵t
𝑥 = Asin⍵t = Asin2πft
v=dx/dt → V= A 2πf cos 2πft
a= dv/dt → a= -A (2πf)² sin 2πft
a= -(2πf)² 𝑥 = -⍵²x
What is the constant of proportionality linking acceleration and displacement?
- ⍵²
theres a minus sign because the acceleration is always in the opposite direction to the displacement
State the equation for velocity used in simple harmonic motion
v = ± ω √(A²– x² )
A- amplitude
x- displacement
State the equation for Vmax and Amax
Maximum velocity : Vmax = ωA
Maximum acceleration : Amax = ω²A
What is an isochronous oscillator?
an oscillator in simple harmonic motion where the period is independant of the amplitude
If the following graph shows displacement against time, what would the velocity-time graph look like?
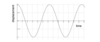
if the displacement graph is displayed as a cosine graph the velocity graph would be the derivative i.e a negative sine graph
If the displacement graph was a sine graph then the velocity graph would be the derivative i.e a cos graph
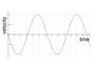
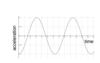
If the following graph shows displacement against time, what would the acceleration-time graph look like?
if the displacement-time graph is demonstrated as a cos graph then the acceleartion-time graph would be its 2nd derivative i.e. a negative cos graph
if it were displayed as a sine graph then its corresponding acceleration-time graph would be a negative sine graph
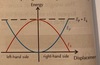
State the interchange between kinetic and potential energy during simple harmonic motion
maximum KE occurs at the equilibrium point , where the velocity is max
maximum PE occurs at the amplitude position, where the displacement is at max
Draw the graph for potential energy and kinetic energy against displacement for a SHM system
Demonstrate how a graph of amplitude against driving frequency would look like
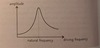
Demonstrate a how a graph of amplitude against driving frequency would look like for a system which has been damped
*notice how damping the system lowers its natural frequency and the amplitude of oscillations
