Number Properties

Question 1

Answer 1

Question 2

Answer 2

Question 3

Is 0 odd or even?

Is 0 positive or negative?

Answer 3

0 is even.

0 is neither positive or negative. Problems often use the phrase “positive integers”– read carefully and realize they are talking about 1, 2, 3…. etc

Question 4

What are the first 10 prime numbers?

Answer 4

2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Question 5

Data Sufficiency:

Is x prime?

(1) x > 2
(2) x is even

Answer 5

Answer is C– Together they are sufficient.

The only even prime is 2. So if x >2 and x is even, the answer to the question is “NO”. Alone each statement is insufficient.

Question 6

Answer 6

Question 7

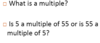
Do the following have the same meaning? Or are any of them different?

a. 3 is a factor of 12
b. 3 is a divisor of 12
c. 12 is a multiple of 3
d. 12 is divisible by 3
e. 12/3 is an integer
f. 12 is equal to 3n, where n is an integer
g. 12/3 yields a remainder of 0
h. 12 items can be shared among 3 people so that each person has the same number of items

Answer 7

Yes, they all have the same meaning!

The GMAT often writes questions in different ways to confuse you.

It’s important to be able to translate the language into something you understand.

Question 8

What is the Least Common Multiple of 18 and 24?

Answer 8

We factor each number and then find the “unique factors” – we find the highest power of each different prime factor and then multiply them.

18 = 3^{<strong>2</strong>} * 2

24 = 2^{<strong>2</strong>} * 3

The Least Common Multiple is 3² * 2² = 72

We can confirm this by writing out the multiples:

18: 18, 36, 54, 72
24: 24, 48, 72

Question 9

Answer 9

Question 10

Data Sufficiency:

Answer 10

Question 11

1) If the units digit of N is 0, what do we know about the factors of N?

Answer 11

1) The factors include 2 and 5, because N must be a multiple of 10.

(For any number we want to factor that ends in one or more 0’s, it is easiest to factor the 10’s out first)

Question 12

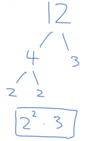
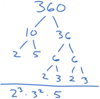
What is the prime factorization of 360?

(Draw a factor tree and then write the exponents)

Example:

Answer 12

Question 13

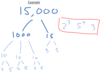
If the integer N ends with “5000”, what do we know about the factors of N?

Answer 13

From the 3 zeros at the end, the factors include 3 pairs of 2’s and 5’s, because N is a multiple of 1000.

Once we factor out 1000, we know that there is another 5 as a factor, since N/1000 would end with a 5.

Factors include 2³ * 5⁴

Question 14

Answer 14

Question 15

Answer 15

Question 16

Answer 16

Question 17

Answer 17

Question 18

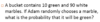
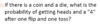
What are Permutations?

Answer 18

Permutations are the number of ways to choose, when order matters.

Ex: How many different license plates can be made, using 3 DISTINCT letters, choosing from the letters A, B, C, D, E, F, G

Write out 3 “Slots”, one for each letter.

___ ___ ___

There are 7 possibilites for the first slot, then 6 possibilites for the 2nd slot, then 5 for the 3rd slot (because the letters must be distinct). We multiply them to find the total number of ways.

_7_ * _6_ *_5_ = 210

Question 19

How many different ways are there to create a code, using 3 DISTINCT digits, using only integers greater than 2 and less than 8?

Answer 19

This is a Permutations problem

How many integers are greater than 2 and less than 8?

3, 4, 5, 6, 7 —> 5 digits

Slots method —> 3 slots —> _5_ * _4\_ *_3\_ = 60

Question 20

The diagram shows the various paths along which a mouse can travel from point X, where it is released, to point Y, where it is rewarded with a food pellet. How many different paths from X to Y can the mouse take if it goes directly from X to Y without retracing any point along a path?

Answer 20

Permutations (we multiply the number of options for each slot/choice/fork)

There are 3 forks along the path: 2 choices for the first one, 2 for the second and 3 for the third.

Total # of ways is 2*2*3 = 12

Question 21

If 4 people each shake everyone else’s hand one time, how many total handshakes are made?

Answer 21

Small numbers, so we could list them. (With larger numbers we would want the formula)

Name them: A, B, C, D. List the pairs:

AB, AC, AD

BC, BD

CD

Total = 6

General formula: 4 people * 3 handshakes made by each person / 2 (because we double counted each handshake–> each handshake is shared by 2 people. AB is the same as BA)