National 5 Waves Flashcards
Factual Recall (38 cards)
What do all waves wave transfer?
All wave transfer Energy
Explain the difference between a transverse and longitudinal wave.
In a transverse wave the particles of the medium oscillate at right angles to the direction of energy transfer.
In a longitudinal wave the particles of the medium medium oscillate parallel to the direction of energy transfer.
Give and example of a longitudinal and a transverse and a wave.
Longitudinal: Sound
Transverse: Water, Light, Radio Waves, All Electromagnetic Waves
Define Frequency
Frequency (f) is the number of waves produced (or passing a point) per second.
It is measured in Hertz (Hz).
1.4 Define Wavelength
Wavelength (greek letter lambda λ) is the length of one complete wave, often measured between successive crests or troughs.
It is measured in metres (m).
For example, A in the image.
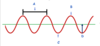
Define the Period of a wave.
The Period (T) of a wave is the time taken to produce for one whole wave.
(One whole crest and one whole trough).
It is measured in seconds (s).
Define the Amplitude of a wave.
Amplitude is the height of a wave from the line of zero disturbance to the top of a crest, or from the line of zero disturbance to the bottom of a trough.
It is measured in metres (m).
For example, D in the attached image.
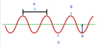
Define the Speed (v) of a wave.
The Speed (v) is the distance travelled per unit of time by a wavefront.
It is measured in metres per second (ms-1).
Define a Crest
A Crest is the highest point of a wave.
For example, B in the attached image.

Define a Trough
A Trough is the lowest point of a wave.
For example, C in the attached image.

Which feature of a wave is measure of its energy?
A Wavelength
B Frequency
C Speed
D Amplitude
E Period
D Amplitude
The greater the amplitude of a wave, the greater its energy.
f = 1/T
(Define symbols and units)
f - frequency (Hz)
T - period (s)
Example
A bat emits ultrasounds with a period of 23 µs. Calculate the frequency of the ultrasound.
T = 23 µs = 23 x 10<sup>-6</sup> s f = ?
f = 1/T f = 1/23 x 10<sup>-6</sup> f = 4.35 x 10<sup>4</sup> Hz
f = N/t
(Define symbols and units)
f - frequency (Hz)
N - Number of waves (no units)
t - time (s)
Example
A siren produces 26,400 waves per minute.
Calculate their frequency.
N = 26,400 t = 1 min = 60 s f = ?
f = N/t f = 26,400/60 f = 440 Hz
v = f λ
(Define symbols and units)
v - speed (ms-1)
f - frequency (Hz)
λ - wavelength (m)
Example
Some water waves have a wavelength of 2 m and a frequency of 6 Hz.
Calculate their speed.
v = ? f = 6 Hz λ = 2 m
v = fλ v = 6 x 2 v = 12 ms<sup>-1</sup>
d = vt
(Define symbols and units)
d - distance (m)
v - speed (ms-1)
t - time (s)
Example
A cannon is 170 m away.
The sound from the cannon firing takes 0.5 s to reach you.
Use this to calculate a value for the speed of sound in air.
v = ? t = 0.5 s d = 170 m
d = vt
170 = v x 0.5
v x 0.5 = 170
v = 170/0.7
v = 340 ms-1
Example
An ultrasound scanner detects an echo from a baby’s head after 0.12 ms.
How far away is the baby’s head?
(Take the speed of sound in tissue to be 1500 ms-1
Don’t forget that in an echo problem the echo has to travel there and back.
v = 1,500 ms<sup>-1</sup> t = ½ x 0.12 ms = ½ x 0.12 x 10<sup>-3</sup> = 6 x 10<sup>-5</sup> s (half for there only) d = ?
d = vt
d = 1,500 x 6 x 10-5
d = 0.09 m
The baby’s head is 0.09 m away.
What is meant by diffraction?
Diffraction is when a wave bends round an obstacle or through a gap.
What are the practical limitations of diffraction?
If an object is small compared to the wavelength, the wave will bend round the object and it cannot be detected.
If a gap is small compared to the wavelength, significant diffraction occurs leading to semicircular wavefronts.
State the effect of wavelength on diffraction.
Longer wavelengths diffract more than shorter wavelengths.
What is meant by the electromagnetic spectrum?
The electromagnetic spectrum is a family of waves which all travel at the speed of light and can travel through a vacuum (no medium required).
They all have different wavelengths and frequencies. All are invisible except visible light.



