National 5 Mechanics Parts 1 & 2 for S3 Exam 2022 Flashcards
- Define what is meant by vector and scalar quantities.
A vector quantity has a magnitude and direction. A scalar quantity only has a magnitude.
- State which of the following list are vector and which are scalar quantities:
force, speed, velocity, distance, displacement, acceleration, mass, time and
energy.
Vector
Force, velocity, displacement, acceleration
Scalar
Speed, distance, mass, time and energy
- State the difference between distance and displacement.
Distance is a measure of how far an object has travelled.
Displacement is the length and direction travelled in a straight line from the starting point to the finishing point.
- Describe how to work out displacement and/or distance using scale diagram or calculation.
For total distance, simply add up the individual distances.
For resultant displacement, sketch a diagram then use Pythagoras (a2 = b2 + c2) to find the hypotenuse, which will be the resultant displacement, and use Trig (tan(x)=Opp/Adj) to find the angle.
- Example of how to work out displacement and/or distance using scale diagram or calculation:
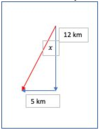
A walker travels 12km South then 5km West. Calculate:
a) the distance travelled
b) the resultant displacement
(See Image)
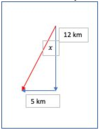
a) d = 12 + 5 = 17 km
b) a2 = b2 + c2
a2 = 52 + 122 = 25 + 144 = 169
a = sqrt(169) = 13 km
tan(x) = Opp/Adj = 5/12
x = tan-1(5/12) = 27º
Bearing is clockwise from North i.e. 180 + 27 = 207º
Resultant Displacement is 13 km bearing 207º
- State the difference between speed and velocity.
Speed is the distance travelled every second and is a scalar.
Velocity is the displacement travelled every second in a certain direction and is a vector.
- Describe an experiment to measure an average speed
You would measure the total distance travelled (d) with a measuring tape and the time taken to cover this distance (t) using a stopwatch. You calculate the average speed (v) by dividing this distance (d) by this time (t).
d = vt
(Define symbols and units)
d - distance (m) or (km)
v - speed (ms-1) or (kmh-1)
t - time (s) or (h)
- Example
You run at a steady speed of 6 ms-1 for 5 minutes. How far did you go?
v = 6 ms<sup>-1</sup> t = 5 min = 5 x 60 = 300 s d = ?
d = vt
= 6x300
d = 1,800 m
d = vt
(Define symbols and units)
d - total distance (m) or (km)
v - average speed (ms-1) or (kmh-1)
t - total time (s) or (h)
- Example
At the 2008 Beijing Olympics, Usain Bolt ran 100m in 9.69 seconds. Calculate his average speed.
d = 100 m t = 9.69 s v = ?
d = v t
100 = v x 9.69
v x 9.69 = 100
v = 100/9.69
v = 10.32 ms-1
s = vt
(Define symbols and units)
s - displacement (m) or (km)
v - velocity (ms-1) or (kmh-1)
t - time (s) or (h)
- Example
James sends a bowling ball off at 8.81 ms-1 North. The first pin is 18.29 m North.
How long does it take for the bowl to hit the pin?
Direction is consistent. Time is a scalar so no direction required.
v = 8.81 ms<sup>-1</sup> s = 18.29 m t = ?
d = vt 18.29 = 8.81xt 8.81xt = 18.29 t = 18.29/8.81 t = 2.08 s
s = vt
(Define symbols and units)
s - resultant displacement (m) or (km)
v - average velocity (ms-1) or (kmh-1)
t - total time (s) or (h)
- Example of how to work out average speed and average velocity using scale diagram or calculation:
A walker travels 12km South then 5km West in 4 hours. Calculate:
a) the distance travelled
b) the resultant displacement
c) the average speed
d) the average velocity
(See Image)
a) d = 12 + 5 = 17 km
b) a2 = b2 + c2
a2 = 52 + 122 = 25 + 144 = 169
a = sqrt(169) = 13 km
tan(x) = Opp/Adj = 5/12
x = tan-1(5/12) = 27º
Bearing is clockwise from North i.e. 180 + 27 = 207º
Resultant Displacement is 13 km bearing 207º
c) d = 17 km; t = 4 h; v = ?
d = vt
17 = v x 4
v x 4 = 17
v = 17/4 = 4.25 kmh-1
d) s = 13 km (207º); t = 4 h; v = ?
s = vt
13 = v x 4
v x 4 = 13
v = 13/4 = 3.25 kmh-1 (207º)
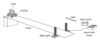
- Describe an experiment to measure instantaneous speed.
You would use a light gate and a mask. Measure the length of the mask (d) with a ruler and the time taken for the mask to go through the light gate (t) using an attached timer. You calculate the instantaneous speed (v) by dividing this distance (d) by this time (t).
- Identify situations where average velocity and instantaneous velocity are different.
Average and instantaneous velocity are different during a sprint race where the runners start from rest then accelerate.
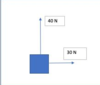
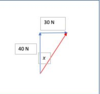
- Describe how to calculate the resultant of two vector quantities at right angles.
Use Pythagoras and Trig:
Draw a diagram, following the head to tail rule. Use Pythagoras (a2 = b2 + c2) to find the hypotenuse, which will be the resultant and use tan(θ) = Opp/Adj to find the angle.
- Example calculation of the resultant of two vector quantities at right angles.
See Image
a2 = b2 + c2
a2 = 302 + 402 = 900 + 1600 = 2500
a = √2500 = 50 N
tan(θ) = Opp/Adj = 40/30
θ = tan-1(40/30) = 53º
Bearing is clockwise from North i.e. 90-53=37º
Resultant Force is 50 N bearing 037º
- Describe how to calculate the resultant of two vector quantities in one dimension.
Sketch a diagram.
Add all the vectors in one direction and subtract all the vectors in the opposite direction.
- Example calculation of the resultant of two vector quantities in one dimension.
Two girls pull a car with a force of 100N each, while friction applies an opposing force of 80N. Calculate the resultant force.
FR = 100 + 100 - 80 = 120N
- Describe how to draw velocity-time graphs or speed-time graphs from data.
Label both axes with quantity and units.
Label the origin.
Draw straight lines for each section of the motion: diagonally upwards for acceleration, straight across for constant speed, diagonally downwards for decceleration.
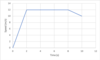
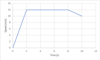
- Example of velocity-time graphs or speed-time graphs from data.
A sprinter accelerates from rest to 12 ms-1 in 2 s, holds this speed steady for 6s, then deccelerates to 10 ms-1 as they cross the line.
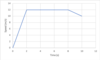
- Describe the motion shown in this graph.
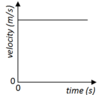
Constant Velocity
- Describe the motion shown in this graph.
Constant Acceleration
- Describe the motion shown in this graph.
Constant Decceleration
- Example: calculate the displacement from this velocity-time graph
s = Area Under Graph
(See Image for identifying triangles and rectangles)
s = ½bh + bh + ½bh + bh
s = ½x2x12 + 6x12 + ½x2x2 + 2x10
s = 106m
- Describe an experiment to measure acceleration.
Ensure that the mask cuts the light gates. Measure the length of the mask (d) using a ruler. Using the timer measure the times for the mask to cut the first light gate (t1), the second light gate (t2) and the time for the mask to travel between light gates (t). Calculate the initial velocity (u) using u=d/t1 and the final velocity (v) using v=d/t2. Calculate the acceleration (a) using a = (v-u)/t.
- Example of how to calculate acceleration from v-t graphs
Calculate the acceleration and decceleration in this motion.
Accleration
u = 0 ms-1
v = 12 ms-1
t = 2 s
a = (v-u)/t
a = (12-0)/2
a = 6 ms-2
Deccleration
u = 12 ms-1
v = 10 ms-1
t = 10-8 = 2 s
a = (v-u)/t
a = (10-12)/2
a = -1 ms-2
- Apply Newton’s Laws to explain or determine a body’s acceleration when more than one force is acting at right angles.
Example:
A toy boat’s engine applies a force of 40N North while river current applies a force of 30N East. The mass of the boat is 20 kg. Calculate it’s acceleration.
Redraw vector diagram nose to tail if required.
a2 = b2 + c2
a2 = 302 + 402 = 900 + 1600 = 2500
a = √2500 = 50 N
tan(x) = Opp/Adj = 30/40
x = tan-1(30/40) = 37º
Resultant Force is 50 N bearing 037º
F<sub>UN</sub> = ma 50 = 20 x a a = 50/20 = 2.5 ms<sup>-2</sup> bearing 037º
- Apply Newton’s 2nd Law to space travel, including rocket launch and landing.
Example:
At launch, a rocket of mass 2000 kg produces a thrust of 25,000 N. Calculate its acceleration.
Draw a sketch diagram, adding in all forces.
Since it moves vertically, we need to add in Weight.
Since it says “At launch” it’s not yet moving, so we can neglect air resistance.
W = mg = 2000 x 9.8 = 19,600 N
FUN = T - W = 25,000 - 19,600 = 5,400 N
F<sub>UN</sub> = ma 5400 = 2000 x a a = 5400/2000 = 2.7 ms<sup>-2</sup> upwards
