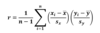Naked Statistics - Charles Wheelen

Question 1

What is a major limit of statistics?

Answer 1

Overreliance on any descriptive statistic can lead to misleading conclusions (p6)

Question 2

What is regression analysis?

Answer 2

A tool that enables researchers to isolate a relationship between two variables while holding constant (or controlling for) the effects of other important variables (p11)

Question 3

What is the point of statistics?

Answer 3

To learn things that inform our lives (p13)

Question 4

What are 7 reasons to learn statistics?

Answer 4

1. To summarize huge quantities of data 2. To make better decisions 3. To answer important social questions 4. To recognize patterns that can optimize processes 5. To catch cheaters and prosecute criminals 6. To evaluate the effectiveness of policies, programs, drugs, medical procedures, etc. 7. To spot those who use statistical tools for nefarious ends

Question 5

What is the mean?

Answer 5

The average of a distribution

Question 6

What is the median?

Answer 6

The point that divides a distribution in half

Question 7

When will the mean and median be similar?

Answer 7

In distributions without serious outliers.

Question 8

What is the difference between “absolute” values and “relative” values?

Answer 8

Absolute values can be interpreted without context, e.g., it’s 80 degrees outside. Relative values have meaning only in comparison to something else, e.g., standardized tests.

Question 9

What is the standard deviation?

Answer 9

A measure of how dispersed the data are from the mean–how “spread out” the observations are. It allows us to assign a single number to the dispersion around the mean.

Question 10

What does a “standard deviation of 18” mean?

Answer 10

A high proportion of observations are 18 above and 18 below the mean.

Question 11

What is a normal distribution?

Answer 11

Data that are distributed normally are symmetrical around their mean in a bell shape.

Question 12

In a normal distribution, what proportion of observations are within one, two, and three standard deviations of the mean?

Answer 12

One standard deviation: 68.2%; two: 95.4%; three: 99.7%

Question 13

What greek letters represent the mean and standard deviation?

Answer 13

Mu and Sigma

Question 14

What is the difference between “percentage change” and “change in percentage points?”

Answer 14

Percentage change always gives the value of a figure relative to something else. Example: a sales tax increase from 3 to 5 percent is two percentage points, but a percentage change of 67%.

Question 15

What is an index?

Answer 15

A descriptive statistic made up of other descriptive statistics, e.g., passer rating, or the S&P 500 index.

Question 16

What is the formula for the variance and standard deviation?

Answer 16

Variance: for any set of observations x1, x2, x3…xn, with mean m, Variance = s^2 = [(x1-m)}^2 + (x2-m)^2 + (x3-m)^2+…(xn-m)^2)] / n Standard deviation: square root of the above (p34-35)

Question 17

Why does calculating the variance put particular weight on observations that lie from the mean–the “outliers”?

Answer 17

Because the difference between each term and the mean is squared. (p34)

Question 18

What does the median versus mean question revolve around?

Answer 18

Whether or not the outliers in a distribution distort what is being described or are instead an important part of the message (p44)

Question 19

What is correlation?

Answer 19

Correlation measures the degree to which two phenomena are related to one another. (p59)

Question 20

What is the correlation coefficient?

Answer 20

An association between two variables expressed as a single number ranging from -1 to 1. The closer the correlation is to -1 or 1, the stronger the association (inverse or direct relation).

Question 21

What is the formula for the correlation coefficient?

Answer 21