Module 1: DFT

Question 1

Main Challenges for DFT

Answer 1

• dispersion forces
  
  • due to long-range correlations between zero-point fluctuations of dipole moments
  • (semi-)local functionals cannot capture this long-range interactions
• overbinding
  
  • usually leads to higher energies, shorter bond lengths, etc.
• self-interaction

Question 2

Dispersion Correction

Answer 2

• correct for dispersion by adding dispersion energy to Kohn-Sham energy
• different methods
  
  • DFTD3
  • TS-vdW
  • vdW-DF

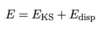
Question 3

Dispersion Energy

Answer 3

• Dispersion energy determined by dispersion coefficients C_x and separation distance r^x
  
  • ​C₆ ≡ vdW/London dispersion
  • calculated analytically using Casimir-Polder formula

Question 4

DFTD3

Answer 4

• uses C₆, C₈ terms to calculate dispersion energy
• use A_mH_n/B_kH_l referece hydrides to compute molecular polarizabilities α(iω) and subtract contribution due to H₂ component
  
  • Requires TDDFT calculations

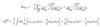
Question 5

TS-vdW

Answer 5

• semi-empirical
• Calculate effective C_6,AB using geometric-like mixing of effective same-species C_6,ii weighted by static polarizabilities
• Effective C_6,ii modified by Hirschfield colume partitioning function

Question 6

Local Density Approximation

(Overview)

Answer 6

• uses per electron exchange-correlation energy of homogeneous electron gas
  
  • exchange known analytically
  • correlation known analytically or numerically exact

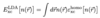
Question 7

Local Density Approximation

(Good Performance)

Answer 7

• structural, elastic, and vibrational properties
• material science

Question 8

Local Density Approximation

(Bad Performance)

Answer 8

• overbinds → binding energies too high
• underestimates lattice constants
• unreliable activation energies for chemical reactions
• energetics of magnetic materials

Question 9

Generalized Gradient Approximation

(Overview)

Answer 9

• enhancement factor F_xc over LDA
  
  • contains next term in derivative expansion of density
• no universal form
  
  • e.g. PBE (Perdew-Burke-Ernzerhof)
• more repulsive core-valence xc → increase in bulk lattice contants
• reduced valence effects → decrease in cohesive energies

Question 10

Generalized Gradient Approximation

(Good Performance)

Answer 10

• atomic and molecular total energies improved
• corrects LDA overbinding
• improved activation energies (still too low, though)
• more relaistic magnetic solids

Question 11

Generalized Gradient Approximation

(Bad Performance)

Answer 11

• softened bonds → increase lattice constants
• dispersion not included

Question 12

Exchange Correlation Exact Definition

Answer 12

• Coulomb interaction between electron at r and value of xc-hole n_xc(r,r’) at r’
  
  • n_xc not known exactly

Question 13

Hybrid Functionals

Answer 13

e.g. B3LYP

Question 14

vdW-DF

Answer 14

• adds non-local term with kernal function

Question 15

TDDFT

Answer 15

• uses Runge-Gross Theorem for quantum mechanical action to define xc energy
• requires new functionals that include (non-)locality in space and time