Module 1

Question 1

Pricing the derivative by forming a replicating portfolio

Answer 1

To form a replicating we use the underlying stock and a risk free bond.

Strategy:

1. ​invest Δ no. of shares in stock and B dollars in a risk-free bond at time 0
2. reinvest all dividends of the stock by buying additional shares. Gives Δe^𝛿h shares at t=h
3. the replicating portfolio at t=h is worth Δe^𝛿hS_h + Be^rh

Question 2

Calculating C_u and C_d

Answer 2

C_u = Δe^𝛿hS₀u + Be^rh

C_d = Δe^𝛿hS₀d + Be^rh

Question 3

Calculating Δ for the replicating portfolio

Answer 3

Note: Δ can be thought of as the sensitivity of the option to a change in the stock price. It will be positive for a call and negative for a put.

Question 4

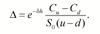
Calculating B for the replicating portfolio

Answer 4

Question 5

Calculating the price of the replicating portfolio at time 0,

C_{<span>0</span>}

Answer 5

Question 6

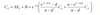
Arbitrage a mispriced option

Answer 6

1. Option overpriced: The price of the option is greater than that of the replicating portfolio, ΔS₀ + B. To arbitrage, we sell the option and buy the replicating portfolio.

• For a call option: We sell the call, buy Δ shares and borrow $B
• For a put option: We sell the put, sell Δ shares and invest $B

1. Option is underpriced: The price of the option is less than that of the replicating portfolio, ΔS₀ + B. To arbitrage, we buy the option and sell the replicating portfolio.

• For a call option: We buy the call, sell Δ shares and invest $B
• For a put option: We buy the put, buy Δ shares and borrow $B

REMEMBER: Buy low, sell high

Question 7

Calculating the risk-neutral probability,

p*

Answer 7

p*: the risk-neutral probability of an increase in the stock price. Used in the risk neutral world. Is not the true probability that the stock price will go up.

Question 8

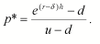
Risk-neutral pricing formula based on a one-period binomial tree

Answer 8

Question 9

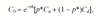
The expectation in the risk-neutral world,

E*

Answer 9

Question 10

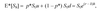
Volatility, σ

Answer 10

The volatility of a stock, σ, is the standard deviation of the stock return

Question 11

Estimating u and d using a forward tree

Answer 11

Question 12

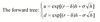
Estimating u and d using a Cox-Ross-Rubenstein Binomial Tree

Answer 12

Question 13

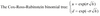
Estimating u and d using a Lognormal/Jarrow-Rudd Binomial Tree

Answer 13

Question 14

Calculating Δ and B for an option on a currency

Answer 14

Where r_f is the foreign risk-free rate and x_o is the exchange rate at t = 0

Question 15

Calculating u and d if the annualized volatility of the exchange rate is given (for a option on a currency)

Answer 15

Question 16

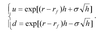
The put-call parity for options on currencies

Answer 16

Question 17

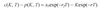
Calculating Δ and B for the replicating portfolio for futures contracts

Answer 17

Question 18

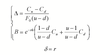
The put-call parity for futures options

Answer 18

Question 19

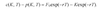
Calculating p* if the annualized volatility of the exchange rate if given (for options on currencies)

Answer 19

p*

Question 20

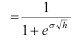
Calculating u and d if a volatility is given (for futures contracts)

Answer 20