Modern Physics: Light Flashcards
(31 cards)
Waves are:
Periodic oscillations of a medium
Important points about waves to remember are:
1) sin(θ) has an amplitude of 1
2) the period of repetition is 2π radians = 360˚
In one dimension, we can write our “wavefunction”, which describes the amplitude of the
wave as a function of position, as follows:
𝜓 𝑥 = 𝐴 sin(2𝜋𝑥/𝜆)= 𝐴 sin(𝑘𝑥)
where we have defined the wavevector k as
𝑘 =2𝜋/𝜆
What is the wavevector K defined as:
𝑘 =2𝜋/𝜆
Note that the units of k are inverse length.
We know that sin 𝜃 = 0 for:
𝜃 = 𝑛𝜋, 𝑛 =1,2,3,…
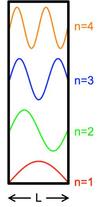
We know that sin 𝜃 = 0 for 𝜃 = 𝑛𝜋, 𝑛 =1,2,3,… This occurs when:
2 𝜋 𝐿/𝜆= 𝑛 𝜋
⇒
𝜆 =2 𝐿/𝑛
⇒
𝜓 𝑥 = 𝐴 sin(𝑛 𝜋 𝑥/𝐿)
We can represent our moving wave as a function of both space and time as:
𝜓 𝑥, 𝑡 = 𝐴 sin(2𝜋𝑥/𝜆−2𝜋𝑡/𝑇)= 𝐴 sin(𝑘𝑥 − 𝜔𝑡)
where we have defined the angular frequency ω as:
𝜔 =2𝜋/𝑇= 2𝜋𝜐
Define angular frequency
𝜔 =2𝜋/𝑇= 2𝜋𝜐
Notice that in one period, the wave moves by one wavelength, so the“phase velocity” is
𝑣 =𝜆𝑇⟹𝜔 = 𝑣𝑘
To complete our definition of the wave, we need
to specify its initial state, usually by setting its value at x=t=0; this is done by introducing a
phase factor φ0. What is the full equation:
𝜓(𝑥,𝑡) = 𝐴 sin 𝑘𝑥 − 𝜔𝑡 − 𝜙)
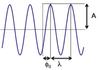
Notice that the complete definition of the wave is given by four independent parameters: A, ω,
k, and φ0. What do these represent?
A= amplitude
ω= angular frequency
k= wavevector
φ0= phase factor
Equivalently, we could also describe a wave by specifying A, T, λ, and φ0. What do these represent?
A= amplitude
T= time phase
λ= wavelength
φ0= phase factor
The power transported by a wave is proportional to..
𝑃 ∝ l𝐴l^2
There are different conventions for how the quantities that determine the properties of waves
are defined and named.
Amplitude
This can be specified as the maximum amplitude 𝐴 or..
the peak-to-peak amplitude (𝐴”” = 2𝐴),
or root mean square amplitude A ‘rms’ = (1/2^0.5)A
There are different conventions for how the quantities that determine the properties of waves
are defined and named.
Period / Frequency
For a given period of oscillation 𝑇, we can specify either the frequency 𝜈 = 1/𝑇 or..
the angular frequency 𝜔 = 2𝜋/𝑇 = 2𝜋𝜈.
There are different conventions for how the quantities that determine the properties of waves
are defined and named.
Wavelength / Wavevector / Wavenumber
For a given wavelength 𝜆, we can specify two corresponding inverse quantities: 1/𝜆 and 2𝜋/𝜆.
Unfortunately, both of these quantities are referred to as wavevector or wavenumber in
different academic fields. In this class, we will use the convention that:
wavenumber refers to
1/𝜆 and wavevector 𝑘 = 2𝜋/𝜆; sometimes the latter quantity is also referred to as the
“angular wavenumber”. Note that the textbook Jewett & Serway uses a different convention
and refers to 𝑘 = 2𝜋/𝜆 as the “wavenumber”.
There are different conventions for how the quantities that determine the properties of waves
are defined and named.
Phase
The sign in front of φ0 can be either positive or negative. If a negative sign is used, a positive
value of φ0 shifts the wave to the right (in the positive x direction); on the other hand, if a
positive sign is used, convention is..
a positive value of φ0 shifts the wave to the left (negative x direction). Either convention is fine as long as it is applied consistently.
The most important point about waves is that they…
obey the principle of superposition.
What does this picture represent?
and what occurs during this interaction?
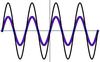
Constructive interference.
𝜓1 = 𝐴 sin 𝑘𝑥 𝜓2 = 𝐴 sin 𝑘𝑥 𝜓3 = 𝜓1 + 𝜓2 = 2𝐴 sin(𝑘𝑥).
The new wave now has zero amplitude because the two components cancel each other. These
two waves are said to be “completely out of phase” or “out of phase” by 180˚ or π radians and
therefore undergo “destructive interference”.
What does this picture represent?
and what occurs during this interaction?

Destructive Interference.
𝜓1 = 𝐴 sin 𝑘𝑥 𝜓2 = 𝐴 sin 𝑘𝑥 + 𝜋 = −𝐴 sin 𝑘𝑥 𝜓3 = 𝜓1 + 𝜓2 = 0
What does this picture represent?
and what occurs during this interaction?

General Interference.
𝜓1 = 𝐴 sin 𝑘𝑥 𝜓2 = 𝐴 sin 𝑘𝑥 +(3𝜋/2) 𝜓3 = 𝜓1 + 𝜓2
If the waves are not perfectly in phase or perfectly out of phase, or do not have the same
frequency, then a more general form of interference will occur.
What is coherence?
If a source emits waves that all have the same phase relationship (i.e. they all have the same
φ0), then the source emits light that is “coherent”. On the other hand, if the phases are all
random, then the source emits light that is “incoherent”.

What is the classical behaviour of light?
Newton originally proposed a “corpuscular” theory of light, in which light is composed of particles. This view was consistent with the development of “geometric
optics”, in which light moves in straight lines, or “rays”.
What does this show?

We see here a profile whose intensity varies as a function of position with a series of maxima
and minima. This behaviour is not consistent with that of a simple particle, but rather seems
like interference, so it is natural to conclude that light must be a wave.