Models Flashcards
(30 cards)
How is a population model generally described?
R(t): growth rate of population over one year
How can constant population growth be described?
What is its solution?
Growth rate of the population over one year R(t) is constant: R(t) = ρ
ρ: constant growth rate
What is the Malthusian population model?
How can it be described?
What is its solution?
Exponential population model.
Growth rate of the population over one year R(t) linearly grows with N(t): R(t) = r * N(t)
with r: intrinsic growth rate
What is Verhulst’s population model?
How can it be described?
What do de parameters represent?
Logistic population model with intraspesific competition (limited resources).
Two possible parametrisations for the growth rate of the population over one year:
- “r-K” parametrisation: R(t) = r * N * (1- N/K)
- “r-α” parametrisation: R(t) = r * N - α * N2
with:
r: intrinsic growth rate,
α: coefficient of intraspecific competition,
K: carrying capacity parameter (lim N(t) = K)

Whats the solution of Verhulst’s model in the “r-K” parametrisation?
How is K represented in a graph of N(t)?
K is the threshold of the population size.
with:
r: intrinsic growth rate,
K: carrying capacity parameter (lim N(t) = K)
What are examples for population models?
Malthusian (or exponential) population model
Verhulst’s (or logistic) population model
What is Kermack-McKendrick’s epidemic model?
How can it be described?
Structured population model
SIR model: Susceptible, Infected & Recovered
with:
S(t): number of susceptible, I(t): number of infected
β: infection rate, α: recovery or death rate

What is Bernoulli’s smallpox model?
Aim to compute life expectancy without smallpox
Is inoculatin beneficial for humanity?
Goal to describe the relationship between the number of survivors with and without smallpox
information/assumptions:
yearly smallpox infection rate (fraction of susceptible people who get infected per year): β = 1/8,
probability of dying from the smallpox once infected: ν = 1/8,
probability of dying from inoculation is 1/200
How can life expectancy be described in general?
with
P(t): number of individuals still alive at beginning of year t > 0, i.e. the so called number of survivors at year t,
P(0): number of newborns

How can the number of survivors without smallpox be described?
with
P(t): number of individuals still alive at beginning of year t > 0, i.e. the so called number of survivors at year t,
β: infection rate, ν: probability of dying from smallpox
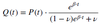
How can the life expectancy without smallpox be described?
with:
Q(t): number of survivors without smallpox
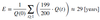
What is the Lotka-Volterra model?
What different vartiations are there?
Interacting populations model with prey and predator
Three main variations:
- Original
- Logistic growth for prey (or predator)
- Functional response (how prey and predator interact)
- Generalised
What is the original Lotka-Volterra model?
How can it be described?
Prey population in absence of predator assumed to increase exponentially and in absence of prey, predator population decreases exponentially
with
N(t): prey population, P(t): predator population,
r: intrinsic growth rate of N, m: mortality rate of P,
γ: attack rate, β: attack rate and conversion (β = γ * ε),
ε: conversion efficiency, in general: β < γ
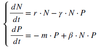
How can the Lotka-Volterra model with logistic grwoth for the prey be described?
with
N(t): prey population, P(t): predator population,
r: intrinsic growth rate of N, m: mortality rate of P,
γ: attack rate, β: attack rate and conversion (β = γ * ε),
ε: conversion efficiency, in general: β < γ,
α: intraspecific competition
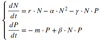
What is the Lotka-Volterra model with functional response?
How can it be described?
Describes how prey and predator interact, by considering the behaviour of a single predator in the system.
with
f(N): functional response, i.e. the number of prey eaten per predator and per unit of time,
N(t): prey population, P(t): predator population,
r: intrinsic growth rate of N, m: mortality rate of P,
ε: conversion efficiency

What is the Rosenzweig-MacArthur model?
How can it be desrcibed?
Functional response that is widely used in theoretical ecology and often with the Lotka-Volterra model with logistic growth of the prey. It is a Holling type II functional response.
with
N(t): prey population, P(t): predator population,
r: intrinsic growth rate of N, m: mortality rate of P,
γ: attack rate, ε: conversion efficiency,
α: intraspecific competition,
Th: handling time (time required to handle a single prey)

What is the generalised Lotka-Volterra model?
How can it be described?
Original Lotka-Volterra model written in matrix notation.
Easy to expand number of species as a set of equations for S species.
with
N(t): prey population, P(t): predator population,
r: intrinsic growth rate of N, m: mortality rate of P,
γ: attack rate, β: attack rate and conversion (β = γ * ε),
ε: conversion efficiency, in general: β < γ,
α: Matrix with intraspecific and interspecific competition

What is the Luria-Debrück model?
Describes resistance of bacteria against bacteriophages.
Two statistical models:
- Contact Hypothesis (Hc): bacterial resistance acquired by contact with virus
- Mutation Hypothesis (Hμ): bacterial resistance acquired by spontaneous mutation
Both transmit resistance to next generation.
Experimental results clearly support Hμ
Number of bacteria at generation time t: N(t) = N(0) * 2t
What are the equilibrium points of Verhulst’s model?
How can their stability be determined?
How does K relate to the equilibrium point?
x-Axis intersections in a Graph of time derivative of population size dn/dt over Population size (N)
Local stability analysis: See if the population returns to the equilibrium point when you move up of down in population size
–> stable: moves back to equilibrium point
–> unstable: moves further away
K is the maximum in population size that is an equilibrium point
How does a trajectory analysis of Verhulst’s model work?
What is the inflection point?
Inverse Graph and draw figure next to it with population size N over time.
Value of horizontal axis of initial graph gives speed at which population size changes.
The inflection point is the maximum of N (second derivative of N(t) equals 0)

What are the equilibrium points of the Kermack-McKendrik (SI) model?
What are the signs of the derivatives?
What is the epidemic threshold?
- *Equilibrium points**: Time derivative of both DE are 0.
- -> Set of equilibrium points: I* = 0 and S* >= 0
Signs:
dS/dt < 0 if S > 0 and I > 0, which is always the case
Epidemic threshold: Epidemic peak reached for: S(t) = α/β
with:
S(t): number of susceptible, I(t): number of infected
β: infection rate, α: recovery or death rate

What is the first integral in the Kermack-McKendrik model?
For what can it be used?
First integral: V(S, I)
- *Note**: V(S(t), I(t)) = V(S(0), I(0))
- -> first integral remains constant for any time t/along the trajectory
- -> Better to take a higher t than 0, because if there are more infected, the error will most likely be smaller
With the above equation we can solve for the epidemic threshold and so by using the fact that α = 1/(Ø days of infection) we can calculate α and β.
And we can determine the value of I(t) at the epidemic threshold by inserting S(t) = α/β into the equation and solving for I(t).
with:
S(t): number of susceptible, I(t): number of infected
β: infection rate, α: recovery or death rate

What are the non-trivial zero growth isoclines for the original Lotka-Volterra model?
What are the equilibrium points?
- *Non-trivial zero growth isoclines**: separate regions with different signs of the derivatives (regions of phase space). They can be determined by setting the DE to 0 and solving for the other species.
- *Prey**: P = r/γ, Predator: N = m/β
- *Equilibrium points:**
- *Trivial**: N* = 0, P * = 0
- *Non-trivial**: intersection of non-trivial zero growth isoclines
with
N(t): prey population, P(t): predator population,
r: intrinsic growth rate of N, m: mortality rate of P,
γ: attack rate, β: attack rate and conversion (β = γ * ε),
ε: conversion efficiency, in general: β < γ
What are the non-trivial zero growth isoclines for the Lotka-Volterra model with logistic growth for the prey?
What are the equilibrium points?
- *Non-trivial zero growth isoclines:**
- *Predator**: N = m/β, Prey: P = r/γ - (α/γ) * N
Equilibrium points: Solve for N* and then calculate P*
N* = m/β and P* = r/γ - (α/γ) * (m/β) = r/γ * (1 - m/(K*β))
with
N(t): prey population, P(t): predator population,
r: intrinsic growth rate of N, m: mortality rate of P,
γ: attack rate, β: attack rate and conversion (β = γ * ε),
ε: conversion efficiency, in general: β < γ,
α: intraspecific competition,
K: carrying capacity parameter (lim N(t) = K)








