Midterm #2 Flashcards
T statistic
used to test hypothesis about unknown popn mean (µ) when **value of σ is unknown **
Formula of:
- T statistic vs. Z statistic
T statistics formula is identical to z-score formula except estimated standard error is used instead of **standard error (σ/√n) **
Estimated Standard Error
Sx-bar = s/√n
- sample standard deviation used instead
**Degrees of freedom **
# of scores in sample that are **independant and free to vary **
The **larger **the value of df….
the more closely t distribution _approximates _normal distribution
t distribution
complete set of values computed for every possible random sample for specific sample size (n) or **specific degrees of freedom (df) **
- approximates shape of normal distribution
One-sample T-test
- formula
- degrees of freedom
df = n - 1
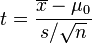
Two-sample Independant T-test
most popular in psychology until early 1960s
- **2-group design: ***treatment *vs. control
- extension of one-sample t-test
Two-sample Independant T-Test
- formula
t = ( x̄1 - x̄2) / √ [(SS1 + SS2)/(n1+ n2 - 2)] (1/n1 + 1/n2)
**Two-sample independant t-test **
- **(3) **assumptions
1) **normality **
2) **homogeneity of variance **
3) independance
Two-sample Independant T-test
- degrees of freedom
- null & alternative hypothesis
df = n1 + n2 - 2
H0 : μ1= μ2
HI : μ1 ≠ μ2
1) normality
difference between popns are normally distributed
2) homogeneity of variance
both samples are drawn from populations whose **variances are the same **
σ12=σ22
3) independance
scores from the 2 populations are independant or **unrelated **
**Two-sample Dependant T-test **
- used in what circumstances?
used for Matching or **Repeated Measures **(Within-subjects) Designs
Matching
- popular strategy in education & developmental psychology
- random assignment = impossible
- address confounds in research
Repeated Measures/Within-Subjects Design
popular in cognitive psychology & learning
- creates **carry-over effects **
- reduces error variance or noise
- statistically complicated
Two-sample Dependant T-test
- **(1) assumption **
normality
Two-sample **Dependant **T-test
- degrees of freedom
- null & alternative hypothesis
df = npairs - 1
Ho: μD = 0
H1: μD ≠ 0
Two-sample **Dependant **T-test
Sample of D scores (difference in scores):
- mean
- sum of squares (SS)
- variance
- standard deviation
- standard error
- **mean: **d-bar = ΣD/npairs
- **sum of squares (SS): **SSd = ΣD2 - (ΣD)2/n
- **variance: ** Sd2 = SSd/(n-1)
- **standard deviation: **Sd = √Sd2
- **standard error: **Sd-bar = Sd/√n `
If you have 3+ levels of a treatment, multiple t-tests would?
How do we **keep **α = 0.05?
inflate **familywise **Type 1 error beyond 5%
use ANOVA
**Analysis of Variance (ANOVA) **
hypothesis-testing procedure used to evaluate mean differences (usually 3+ levels) between 2+ treatments
**One-Way ANOVA **
technique used for **3+ **treatment levels/samples
- n must be equal for each
- employs Fisher (F) distribution
- negativeF values = impossible
- **positively **skewed
- considered an **Omnibus test **
One-Way ANOVA
- ideal case for rejecting Ho?
**large **variability between treatments but **small **variability within each treatment
**One-Way ANOVA **
- what values needed?
SStotal
SSwithin
SSbetween
MS (mean square)
Fobtained
Fcritical
df
One-Way ANOVA
- calculating SS
- calculating MS
SSt = Σx2 - (Σx)2/N
SSw = Σx2 - (ΣxA)2/n
SSb = SSt = SSw
MS = SS/df
One-Way ANOVA
- degrees of freedom
- F values
(a = # of treatments)
**dfb **= a - 1
dfw = a (n-1) = N - a
dft = dfw + dfb = N - 1
F<strong>obtained</strong>= MSb/MSw
Fcritical
- dfnumerator= dfb
- dfdenominator= dfw
If 3+ treatments for one-way ANOVA…
**post-hoc **test **required to determine source of difference
**Post-Hoc Test **for ONE-WAY ANOVA
Tukey Honest Significant Difference (HSD)
Tukey Honest Significant Difference (HSD)
**Tukey HSD = q √ (MSw/n) **
q = studentized range statistic (Table B.5)
df for error term = dfw
k = # of treatments
