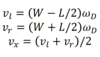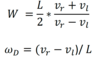Midterm 1: Week 1 to 6 Flashcards
What is an intelligent robot?
Intelligent robots are devices made of hardware and software.
The primary structure of intelligence in a robot is the sense-plan-act loop that allows reaction to the surrounding world.
Sense-plan-act loop
Sense: Gather information
Plan: Take the information and come up with a series of behaviours to do something
Act: perform the plan
State Space
Set of all physical situations that could arise. It captures the meaningful properties of the robot.
Notice that determining the correct representation of the state space is the #1 task of a roboticist.
Action Space
The commands, forces or other effects it can take to change its own state or that of the environment.
Notice that the action space can be state-dependent.
Kinematics
Considers constraints (limitations) on the state space and how we can transition between states.
A more formal definition is the following:
Kinematics describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move.
Dynamics
Consider idealized physics of motion.
- Forces
- Control
Model
A function that describes a physical phenomenon or a system. Models are useful if they can predict reality up to some degree.
Mismatch between the model prediction and reality is called noise/ error
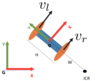
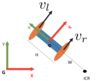
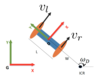
Omnidirectional Robots
Robots that can move in any direction without necessitating to rotate.
State of an Omnidirectional Robot
Control of an Omnidirectional Robot
Notes on Inertial frames of reference
G the global frame of refrence is fixe i.e. with zero velocity in our previous example.
- If a robot’s position is known in the global frame, life is good!
- I can correctly report its position
- We can compute the direction and distance to a goal point
- We can avoid collisions with obstacles also known in global frame
Kinematics as Constraints
Notice that the idea of using vector spaces or set to represent everything that can happen is too broad to capture robot details.
A common form of kinematics is to state a ser of constraints also. These can be on the allowable states or how to move between states.
Kinematics of a simple car
State
Kinematics of a simple car
Control
Kinematics of a simple car
Velocities
Instantaneous Center of Rotation
The centre of the circle circumcises by the turning path.
Undefined for straight path segments.
The Dubins Car Model
Visualize a car that can only move forward at a constant speed s and with a maximum steering angle
First Robotics Theorem
The shortest paths of the Dubins Car can be decomposed into:
L: max left turn
R: max right turn
S; zero turn
*This rules out to ever turn partially
Motion Primitives
The fixed motion types: L, R, S, are called primitives. We can use them to decompose a series of motions to reach a goal.
Dubins Airplane
State of a Unicycle
Notice, here the state is the same as for the car and the omnidirectional robot since here we are just interested in the Global position of the unicycle.
x = [G_p_x, G_p_y, G__(teta)]
Controls of a Unicycle
We consider the angular vellocities on y and z.
On z it is how fast the wheel turns. On y it is how much it turns on the plane.
Recall that the control set of a unicycle includes the angular velocities on y and z. How do you calculate the velocities of an unicycle?
State of a different drive vehicle
Same as the car, omnidirectional robot and unicycle
Control of a different drive vehicle
In this case, we look at the velocity or turning rate of each wheel.
The turning rate of each wheel will determine the direction and force applied on the vehicle.
What are the velocities of this vehicle?
Holonomic kinematics
A system that constraints only on its position. That is, it has a bounded state-space, but no limits on its differential motions.
Intuition: You can immediately move in any direction you would like.
Notice that a holonomic robot can guarantee that fairly simple math can yield to optimal paths
Non-holonomic kinematics
A system that has at least one non-trivial constraint on its differential motions.
Intuition: It is possible to get someplace nearby eventually, but not in a single step.
Notice that for a non-holonomic robot we might require arbitrarily many motions to move a small distance.
Which of the following are non-holonomic?
- A normal car
- A robot train that can go forward and backwards on a circular track
- A robot train that can only go forward on a circular track
1 and 3 are non-holonomic
Consider the Differential Drive Vehicle.
Derive the equations that represent the velocity on the right, left wheels and on the x-direction.
How do we find the velocity when rotating?
v = r * w where w is the angular velocity.
So, if w_D is the angular velocity, we have to find the radius.
In the case of a Differential Drive Vehicle, if we know the different velocities we can find the angular velocity w and the distance from the ICR to the centre fo the vehicle,
how?
In the case of a Differential Drive Vehicle, what happens if
v_r = v_l
The direction of the car would be straight.
In the case of a Differential Drive Vehicle, what would happen if:
v_r = -v_l
Then the centre of the vehicle D would be ICR.
In the case of the differential drive vehicle, write the equations to find the x, y position and the angle depending on the Global coordinate system.
G_p_x (t + 1) =
Forward Kinematics (fkine)
What is the robots state given a command/control?
Kinematics directly tell us how to compute:
- position
- speed on various frames
- turning rate
All this in function of the input commands
Inverse Kinematics (Ikine)
What control(s)bring us to the desired state (if any)?
Inverse kinematics is like a “short time” plan. Depending on the form of the model, this can be easy or difficult to find.
When would it be easy or hard to find an inverse kinematics solution?
When the robot is non-holonomic it would be harder to find an inverse solution.
What is the motion to bring the body of a DD vehicle from (10,10,pi/4) to (0,0,0)?
- Follow right angle: (10,10) - > (10.0) -> (0,0)
- Point then Shoot: turn the car to destination and go straight line
Point then Shoot
First rotate to face the point, drive straight to the point, then rotate to goal angle
Robot’s Dynamic Equations
A robot’s dynamic equations form an equation that determines its motions in response to any possible action.
They include the geometric properties from kinematics, but also dynamic quantities: weight, motor strength, material composition, etc.
What does x with a dot above mean?
An “overdot” is a raised dot appearing above a symbol most commonly used in mathematics to indicate a derivative taken with respect to time
Forward Dynamics
Describes how an object moves in time, from initial conditions, following applies forces.
What is the dynamic equation of a pendulum under gravity?
Where:
- I = mL^2 (inertia)
- m = mass
- g = gravty
- L = length of string of the pendulum
- teta =angle from vertical axis to inclination of string
Pendulum Trajectory
See lecture 3, recording from 48min to 54min
What do we have to add to the pendulum’s dynamic equation if we want it to act as a robot?
We have to have some way yo control it. We have to add the control.
By adding control we can now hold the pendulum stationary, build energy, reduce energy.
Double-Link Pendulum
State:
x = [teta1, teta2, teta.1, teta.2] The angle or joint 2 is expressed wrt joint 1.
Controls:
u = [torque1]
Dynamics: Slide 24 Lecture 3
TODO week 2 and 3
Name some drawbacks of Grid based planners
- They work well for grids up to 3 to 4 dimensions
- State-space discreization suggers from combinatorial explosion:
- if x=[x_1,…., x_D] and we split each dimension into N bins then we will have N^D nodes in the graph
- See notes on Sept. 22nd
- if x=[x_1,…., x_D] and we split each dimension into N bins then we will have N^D nodes in the graph
- This is not practical for planning paths for robot arms with multiple joints or other high-dimensional systems
What do we have to do to avoid the problems that arise with the grid based planners?
We need to find ways to reduce the continuous domain into a sparser graph. One that covers the same space with fewer nodes and edges.
Cell Decomposition Planners
Idea:
Decompose the overall planning process into local regions.
Simple computations can tell us the path through the region.
A global computation can be performed to re-assemble the entire path, and often we can re-use our local computation for multiple queries.
Visibility Path
In this method, the objects are considered to be polygones.
- Draw lines of sight from the start and from the goal to all vertices of the polygones. (slide 7)
- Draw the lines of sight from every vertex of every obstacle (as done in 1). Remember that the lines that follow the edges of an obstalce are also considered as lines of sight.
- Repeat until you are done
Notice: when you add lines, the lines cannot go over an obstacle
Visibility Path:
Search Algorthms
- Opened vertices = {start}
- Repeat until done:
- Add edges from opened vertices to visible obstacles
- If goal visible from latest vertex added then done!
Can you proof or disproof the following?
The optimal path in a 2D polygon map is the lowest cost path within the visibility graph.
Start with knowledge that the shortest path in free spae is a straight line. Without obstacles, we are set.
Now, consider a path that hits the obstacle anywhere other than its corner, but still passes beyond this obstacle. Can this be shorter?
Yes! If the obstacle is hit in the middle of an edge, then we have to get to one of its vertecies to turn around it, but if we directly get to a vertex, this path is shorter.
True or False
The Visibility Graph is optimal in all dimensions.
False,
Visibility graphs do not preserve their optimality in higher dimensions.
See image.
Rapidly Exploring Random Trees
Main Idea:
Maintain a tree of reachable configuration from the root.
Steps:
- Sample random state
- Find the closest state (node) already in the tree
- Steer the closest node towards the random state
RRT Algorithm
- V <— {x_init}; E <– empty;
- for i = 1, …, n do
- x_rand <— SampleFree_i;
- x_nearest <— Nearest(G = (V,E), x_rand);
- x_new <— Steer(x_nearest, x_rand);
- if ObstacleFree(x_nearest, x_new) then
- V <— V union {x_new}; E <— E union {(x_nearest, x_new)}
- return G=(V,E);
RRT Algorithm
SampleFree()
SampleFree() needs to sample a random state from the uniform distribution.
How do we sample rotations uniformly?
Notice that to sample in lets say Python, you could use the rand function. If you are sampling between two values they you would have to multiply by them.
RRT Algorithm
Nearest()
Nearest() searches for the nearest neighbour of a given vector. Brute force search examines |V| nodes (increasing).
Is there a more efficient method?
We will see in next lectures
RRT Algorithm
Steer()
Steer() finds the controls that take the nearest state to the new state. Easy for omnidirectional robots.
What about non-holonomic systems?
In this case, you will have to consider kinematics in the Steer() function.
RRT Algorithm
ObstacleFree()
ObstacleFree() checks the path from the nearest state to the new state for collisions.
How do you do collision check?
We have do check for collisions.
Name an updside of using ObstacleFree()
You don’t need to model obstacles in Steer().
For example, if Steer() computes optimal controllers that we’ll learn about soon, you don’t need to model obstacles in the control computation.
Collision Detection
Main idea:
When obstacles are complex, this is a problem for run-time. Bounding volume collision detection uses a simple shape for a quick check, eliminate most obstacles easily.
Finding the Nearest Neighbour
Besides brute force search, there is space partitioning and locality-sensitive hashing
Space partitioning
Divide the space into two and check the distance of the points. Remember in which side of the graph the point is and add to a tree.
This is called kd-trees
Locality-sensitive Hashing
- Maintain buckets
- Similar points are placed on the same bucket
- When searching consider only points that map to the same bucket.
RRT Connect
We grow two trees, one from START and the other one from GOAL.
Each time we create a vertex, we try to greedily connect the two trees.
See example slides 28 -64
RRT
Properties of the Planning Algorithm
- The RRT will eventually cover the space i.e. it is a space-filling tree
- The RRT will NOT compute the optimal path asymptotically
- The RRT will exhibit “Voronoi bias”
- The probability of RRT finding a path increases exponentially in the number of iterations
- The distribution of RRT’s nodes is the same as the distribution in SampleFree()
Slides 72, 73 ?
Why do we bother with the problem of following a wall or a line?
It allows for arbitrary path following where the wall is replaced by a local line tangent to the curving path
In control, we will add the idea of parametrized goal or reward function.
Why do we do this?
x = g goal
or r(x) reward
By changing the goal or setting a different reward, we can “retarget” the behaviour of our planning logic.
IMPORTANT: The goal might change over time!!!
Double-link Inverted Pendulum
Trajectory Control
To get the pendulum to be in equilibrium on top of the table, the pendulum will ususally swing back and forth multiple times to gain momentum.
Why can’t we just get to the desired position in one swing?
How many swings do we need?
Once it is in balane, there has to be accurate motion and robust to disturbance to keep the balance
At this point we also start sending feedback. Motions have to correct the small errors and for this the dynamis aren’t that simple!
Control Formulations
Dynamics is governed by the equations of motion of our robotic system.
dx/dt = f(x, u)
where x = pos, vel u=forces, acceleration
Controller
A controller chooses u = π(x) dependent on state and time to move the system to the goal state x=g and keep it there , to follow a trajectory specied by the user (or system componenent).
The game is producing the form and details of π
π gives you control given state and dynamics.
Underactuated
Depending on properties of system dynamics dx/dt = f(x,u), we might not be able to choose x directly.
Controllable
We can control the system from ay initial state to any final state in a finite time.
Control Goals
- Time-respose characteristics:
- rise/response time
- Settling time
- Oscillation period
- Feasibility:
- Given a dynamic robot and a finite set of controllers. is it possible that a controller will reach the goal?
- Stability:
- When you reach the goal. you will stay within a small range forever
Control Theory Results
- Important results:
- bang-bang
- PID
- Probably optimal solutions under correct assumptions:
- LQR
- Approximations and analysis tools
- Trajectory optimization
- Know nothing about the model
- Reinforcement Learning
What does it mean to have the “best” policy?
- In this case, instead of having a goal, we give a reward and we want to find the policy that optimises that reward.
- In other words, we want to minimize a cost function that tell us how “bad” each wrong answer is.
- This allows us to think ahead of time and solve for trajectories that minimize the sum of costs ad we formulate their matching control.
Double Integrator
(Block on ice)
Goal: Move the block to some target point
WLG: assume that goal is (0,0)
The name comes from the fact that we directly influence force ~ acceleration d2x/dt2
The dynamic must be integrated twice.
Pasive dynamics
Corresponds to a taxi sliding on roads. It just slides.
Controlled Dynamics
What about the controlled dynamics of a limited double integrator?
in this case we limit the force!
How does the Double Integrator (DI) evolves in terms of x and dx/dt?
First, notice that there is no friction and that the mass of the block is 1:
Map
- A map of the environment adds external constraints on the where the robot can be
- Maps can be given to the robot or we can build the robot with sensors
- A map should relate to the robot’s state space
Plan
Sequence of states for a robot within a map.
A plan is feasible if eahc state in the sequence and the motion netween consecutive pairs are all feasible under the kinematics and the map.
Planning algorithms can be:
- Correct if every plan they output is feasible
- Complete if they find a plan whenever one exists
Planning algorithm for Dubin’s car
Input:
- Map
- current state
- goal state
Output:
- A plan, as a sequence of states that follow Dubins constraints, if one exists
- A “fail” flag if not
Full Arm Dynamics
Forward Dynamics:
Notice that to find the robot’s path in space you would have to integrate twice!
This is usually not done by hand. There are ODEs solvers that can help with this.
Important Dynamics Properties
Stability: Does the system diverge or converge over time in a certain region?
Controllability: for all x in the state spacem is there at least one action trjectory that allows us to reach x?
Fully actuated: for all feasible acceleration directions a, does an action exist that allows us to accelerate along a?
Controllability
- A system is controllable if there exist control sequences that can bring the system from any state to any other state, in finite time
Underactuated
Robot that is not able to command an instantaneous acceleration in an arbitrary direction
Control the Robot’s motion
Here, planning will be concerned with kinematics and sequence states that reach a goal.
Control is oncerned with computing actions, that lead the robot along the plan or satisfy some criteria.
Forward Kinematicks
What robot state results from a given control.
Input: Control
Output: State
Inverse Kinematics
Which control(s) brings us to a desired state (if any)?
Input: desired state
Output: Control or sequence of controls
Forward Dynamics
What robot motion will result from given forces?
Input: forces
Output: motion
Inverse Dynamics
Which input force(s) will result in a desierd robot motion (if any)?
Input: desired robot motion
Output: force or sequence of forces
Note on Inverse Kinematics and Inverse Dynamics
The inverse problems are more interesting, but depend on the form of the forward model.
Single-link Cartpole
State:
x = [px, dpx, theta, dtheta]
State = [position and velocity, orientation and angular velocity]
Controls:
u = [f]
controls = [horizontal force applied to cart]
Quadrotor
State = [roll, pitch, yaw, and roll rate, pitch rate, roll rate] wrt to G
Control = [T1, T2, T3, T4] = [Thrusts of four motors]
OR = [M1, M2, M3, M4] = [Torques of four motors]
See Lecture 3 slides 38,39
Passive Dynamics
Dynamics of systems that operate without drawing (a lot of) energy from a power supply.
Usually propelled by their own weight
Incoming data for robots
A robot’s sensors give it feedback on its internal state (proprioception) and allow it to observe the external world (exteroception)
Notice that sensors are not perfect.
Sensors
Devices that can sense and measure physical properties of the environment.
To transmit the information, the key pheomenon is transduction.
Notice that measurements are noisy! Thus, sensors are not perfect.
Transduction
Conversion of energy from form to another
The Bug Algorithm #1
- Move in a straight line path towards G
- If the robot reaches G, we are done
- If the robot hits an obstacle, then follow the righ-hand rule and traverse its boundary
- Continue until the wall is no longer pointing agains the straight line from X toward G. Once this occurs, continue from Step 1
The Bug Algorithm #1 Counter example
The Bug Algorithm #2
- Move in a straight line path toward G
- If the robot reaches G, we are done
- If the robot hits an obstacle, remember the point P at which it is hit and follow the right-hand rule
- If the robot crosses the line PG as it walks along the wall of the obstacle, determine wheter ||X - G|| < ||P - G|| and the and the wall is not pointing against the straight line from X toward G. If both condition are satisfied, continue from step 1. Otherwise, keep walking.
- If P is reached again, return “No path”
Proof the Bug #2 is complete
- For each obstacle, Bug 2 will break away from it at some point if there is a path to the goal.
- The sequence of hit points decreases in distance to the goal
- If there is no path to the goal, then Bug 2 will terminate correctly with failure.
What is a plan?
Informally:
- Intuitively, a plan is a path from start to goal.
- The robot should be able to follow this path under its kinetics
- The path should not take the robot through any obstacles in the map
Formally:
- Plan is a sequence of states: P = {x0,x1,x2,…, xn}
What is a feasible plan?
A feasible plan is one where
- x0 = S (start)
- xn = G (goal)
- Each state xt is in free space
- Each transition between subsequent states, (xt, xt+1) obeys kinematics
Feasibility of states and transitions involves kinematics and maps
Planning Algorithms
Planning algoriths:
Input: Start, Goal, Map, Kinematic constraints
Output: plan or “impossible”
Planner Properties
Planning algorithms are:
- Correct if every plan they output is feasible
- Complete if they fins a plan whenever one exists
- Terminating if they execute in a finite time
The complexity is measured by the worst-case memory and run-time in the map/robot dimensions, path length, etc.
Planning as Graph Search
- Graph nodes represent discrete states
- Edges represent transitions/actions
- Edges have weights
Typical assumptions:
- Current state is known
- Map is known
- Map is mostly static
How do you build your graph from a map?
- Nodes are every place in space
- Edges are drawn between neighboring places that are reachable under the kinematics
- A path from start to goal is a list of nodes and edges
Forward Search
Dynamic Programming
Dijkstra’s Algorithm
- Let D(v) denote the length of the optimal path from the source node to the node v.
- Set D(v) = infinity for all nodes except for the source node for which D(v) = 0
- Add all nodes to Q
- While Q is not empty
- Get v with min cost D(v)
- If v = goal, then done
- For u in Ngd(v):
- if d(u,v) + D(v) < D(u)
- then update priority of u in priority queue Q to be d(u,v) + D(v)
- if d(u,v) + D(v) < D(u)
In Dynamic programming what is the Worst-case complexity?
O(|V|2)
What is the downside of Dijkstra’s algorithm?
In a grid map, there are many nodes that are explored unecessarly. We are sure that they are not going to be part of the solution.
ex: nodes that get away from the goal.
What is the upside of Dijkstra’s algorithm?
Always gives an optimal solution.
A* Search
Main idea
- modifies Dijkstra’s algorithm to be more efficient
- Expands fewwer nodes than DIjtra’s by using a heuristic
- While Dijkstra prioritizes nodes based on cost-to-come A* prioritizes them based on:
- cost-to-come to v + lower bound on cost-to-go from v to v_dest
- f(v) = g(v) + h(v)
- f(v) is the lower bound on cost of path from source to destination that passes through v
- Notice: this is an optimistic search since we explire the node with the smallest f(v) next.
A* Search Algorithm
- Set g(v) = infinity for all nodes except for source g(vsrc) = 0
- Set h(v) = infinity for all nodes except for source f(vsrc) = h(vsrc)
- Add vsrc to priority queue Q with priority f(vsrc)
- While Q is not empty:
- extract v with minimum f(v) from the queue Q
- If found goal then done. Follow the parent pointers from v to ge the path.
- Remove v from queue Q
- explored(v) = true
- For u in neighborhood of v if not explored(u)”
- if u not in Q then
- Add u to Q with cost to come g(u) = g(v) + d(v,u) and priority f(u) = g(u) + h(u)
- Set parent of u to be v
- else if g(v) + d(u,v) < g(u)
- Update the cost-to-come and the priority of u in Q
- Set the parent of u to be v
- if u not in Q then
Is RRT complete?
- Noticed that since it is randomized this is not obvious
- For this we need probabilistic completeness
Probabilistic Completeness
The probability that the planner returns a feasible solution, if one exists, converges to 1.0 as the number of samples tends to infinity.
Proof or disproof:
RRT is probabilistic complete.
This is a straightforward consequence of the claims on the previous slide.
What is the run-time complexity of planning from A to B with RRT?
- the answer is that it is “mostly” independent of the planning dimensionality.
- This depends on how we implement collision/free checing and nearest neighbor query independent of dimension
- Does dependent on the “tube” surrounding feasible solutions. Essentially, how often will we randomly sample something helpful?
Probabilistic Roadmaps (PRMs)
- Notice that RRTs are good for single-query path planning
- If you want to find the path from another A to B, you have to re-plan from scratch.
- PRM addresses this problem.
- It is good for multi-query path planing
PRM Algorithm
Notice that to perform a query A -> B, we need to connect A and B to the PRM. We can do this by nearest neighbor search.
What is our optimal controller?
