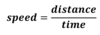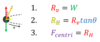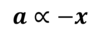Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Jen's B-Block > Mega Deck > Flashcards

Mega Deck Flashcards

1
Q

State two conditions for any object to be in equilibrium

A

Resultant force zero
Resultant moment about any point zero

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

State three vector quantities

A

Any 3 of the following:

Velocity
Acceleration
Force

Displacement

Weight

Momentum

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

State three scalar quantities

A

Any 3 of the following:

Speed
Distance
Mass

Energy

Power

Temperature

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

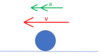
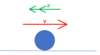
How can force vectors be arranged to show that an object has constant velocity?

A
  1. Vectors make a closed shape when rearranged (by scale drawing)
  2. Or resolve into components and show
  • Total up forces = Total Down forces
  • Total left forces = Total right forces
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

What is the difference between a vector quantity and a scalar quantity?

A

Vector has a direction
Scalar does not

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What is meant by centre of mass?

A

The point in a body where the weight of the object appears to act

Also the resultant moment about this point = 0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Define the moment of a force

A

Product of the force and the perpendicular distance from the line of action of the force to the point

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

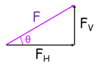
Resolve F into its vertical and horizontal components…

A

FH = FcosØ

Fv = FsinØ

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

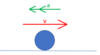
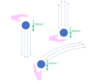
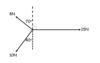
What mistake has been made in rearranging the vectors for a scale drawing?

A

6N vector has been translated (moved) but also rotated

Should be:

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

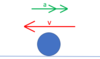
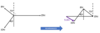
What are the steps in working out the resultant force using a tip-tail scale drawing?

A
  1. Set a scale
  2. Draw the horizontal or vertical vector first (if there is one)
  3. Move each vector in turn to the end of the previous one (DO NOT ROTATE THE VECTORS)
  4. Resultant vector goes from the very start to the very end
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

How is the balancing force different from the resultant force?

A

The balancing force brings the object into equilibrium so makes the resultant force = 0

For a scale drawing, it is the vector that closes the shape

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

If vectors are parallel they can be resolved by…

A

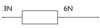
Adding or subtracting the values

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

If vectors are perpendicular they can be resolved by…

A

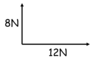
Making a right angled triangle and using trigonometry and pythagoras

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

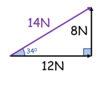
What is wrong with this?

A

Vectors of different types can’t be combined

(Here, force and velocity cannot be combined)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

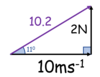
How do you solve this if the object is in equilibrium?

(3 vectors with 2 unknown sizes)

A
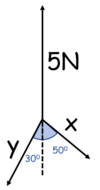
  1. The vectors must form a closed shape
  2. Start as you would with a scale drawing
  3. But draw the third vector meeting for where it connects to the start of the first
  4. Draws vectors as dotted lines

(x=2.54N, y=3.89N)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

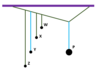
The box is in equilibrium with no external forces applied

Label the forces acting on the box

A

Notice the angle between weight and perpendicular is also Ø

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

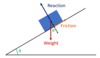
How do you calculate the resultant moment? (2 ways)

A
  1. Multiply perpendicular component of force by distance
  2. Multiply perpendicular component of distance by force

(First method is shown)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

What’s wrong with this?

A

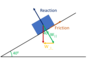
Weight must form the hypotenuse of the triangle

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

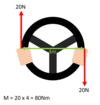
What is a couple?

A

A pair of equal and opposite coplanar forces which do not act along the same line of action

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

What does it mean if an object is uniform?

A

It has an constant density so its centre of mass acts from the physical centre point of the object

(Weight vector starts from middle of object)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

When should you use moments?

A

Any situation that has two unknown forces acting on an object

Take moments about one of the unknown forces to find the other

Then use total up force = total down force to find the other

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

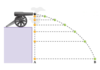
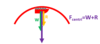
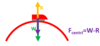
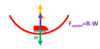
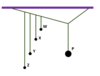
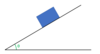
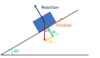
If this box is in equilibrium how would you go about calculating the frictional force and the reaction force?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

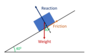
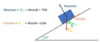
State the principle of moments

A

Sum of the clockwise moments about a point is equal to the sum of the anticlockwise moments for a system in equilibrium

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

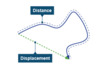
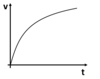
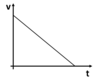
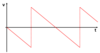
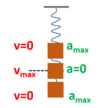
What is displacement and how is it different to distance?

A

Displacement is a measure of the line connecting the starting point to the finishing point.

Distance is a measure of the total length of the path travelled.

Also distance is a scalar and displacement is a vector.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

What does a straight line on a distance-time graph represent?

A

A constant speed.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

How is acceleration defined?

A

Acceleration is the rate of change of velocity.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

How is speed different to velocity?

A

Speed is the rate of change of distance.

Velocity is the rate of change of displacement.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q

Describe the motion of this ball

A

Ball is moving to the right and speeding up.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q

Decribe the motion of this ball.

A

Ball is moving to the left and speeding up.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q

Describe the motion of this ball.

A

Ball is moving to the right and slowing down.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

Describe the motion of this ball.

A

Ball is moving to the left but slowing down.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q

Is the ball moving to the right?

A

Only if the velocity vector is also acting to the right.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q

What does a straight line on a displacement-time graph represent?

A

A constant velocity.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
35
Q

What does a curve with an increasing gradient represent on a displacement-time graph?

A

An increasing velocity (acceleration)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
36
Q

What does a curve with a decreasing gradient represent on a displacement-time graph?

A

A decreasing velocity (decceleration)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
37
Q

What does a negative gradient on a displacement-time graph represent?

A

A negative velocity (travelling back to where it started)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
38
Q

What does a straight line on a velocity-time graph represent?

A

A constant acceleration.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
39
Q

What does a curve with an increasing gradient represent on a velocity-time graph?

A

An increasing acceleration.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
40
Q

What does a curve with a decreasing gradient represent on a velocity-time graph?

A

A decreasing acceleration.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
41
Q

What does a negative gradient on a velocity-time graph represent?

A

A negative acceleration.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
42
Q

What does this graph show?

A

A ball bouncing off a surface

(Dotted lines represent the bounce)

(Red lines represent the ball accelerating towards the ground)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
43
Q

What does the acceleration time graph of a ball in freefall look like?

A

Constant acceleration of 9.81ms-2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
44
Q

What does the area of a speed-time graph represent?

How about a displacement-time graph?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
45
Q

What’s wrong with this?

A

Displacement takes direction into account.

It should be…

46
Q

When can you use this equation?

A

When the acceleration = 0 (constant velocity)

Ot to work out an average speed

47
Q

When can you use SUVATs?

A

When acceleration is constant

Or if obejct has stages of constant acceleration

48
Q

Why can’t you use SUVAT’s when working with this graph?

A

Because the acceleration (gradient) is changing

49
Q

What does it mean if an object is in freefall?

A

Only weight is acting on the object

It has a constant acceleration of 9.81ms-2 acting downawards (on Earth)

50
Q

If one ball is dropped as another is projected horizontally which hits the ground first?

A

They both hit the ground at the same time…

Both in freefall so accelerate at 9.81ms-2

Vertical motion independent of horizontal motion

51
Q

What’s wrong with this labelling?

A

Initial velocity and final velocity are not 0

52
Q

In projectile motion when is the vertical component of the velocity 0?

A

At the peak of a parabola

Not at the start or end

53
Q

How do you start a question involving angled projectile motion?

A

Resolve the velocity into vertical and horizontal components and fill out the corresponding SUVATs

54
Q

What is wrong here?

A

The acceleration is only 9.81ms-2 if the object is in freefall

55
Q

What is the term given to an object rotating at a steady rate?

A

Uniform circular motion

56
Q

If an ball on a string is travelling in a circle in the vertical plane, where are the points of minimum and maximum tension?

A

Minimum tension at the top
Maximum tension at the bottom

58
Q

Why do planes turn when at an angle?

A

The lift force is comprised of a horizontal and vertical component.
The horizontal component provides the centripetal force causing it to turn.

59
Q

Define centripetal force

A

The resultant force that makes the object move in a circle

61
Q

What kind of motion will a pendulum perform?

A

Simple harmonic motion

62
Q

What is the period of oscillation?

A

The time for one complete cycle of oscillation.

63
Q

If the graph of displacement is sin(x), what will the respective graphs of velocity and acceleration look like?

A

Velocity as cos(x)
Acceleration as -sin(x)

64
Q

Describe a freely oscillating object

A

It oscillates with a constant amplitude because there is no friction acting on it.

(Its energy is constant)

65
Q

What is natural frequency?

A

The frequency of free oscillations of an oscillating system.

66
Q

What are forced vibrations?

A

Making an object oscillate at a frequency that is not it’s natural frequency

67
Q

When does resonance occur?

A

When the frequency of driving force or oscillation matches the natural frequency of the system.

68
Q

What is the outcome of resonance?

A

An increase in amplitude of the system’s oscillation.

69
Q

What is damping?

A

The term used to describe the removal of energy from an oscillating system.

70
Q

Describe heavy damping (over damping)

A

System not allowed to oscillate.

Slowly returns to equilibrium.

71
Q

Describe critical damping

A

The oscillating system returns to the zero position of the oscillation after one quarter of a time period.

72
Q

How do you convert degrees -> radians

A
73
Q

How do you convert radians -> degrees

A
74
Q

Define angular displacement

A

The angle through which an object in circular motion travels in a given time

75
Q

What are the three levels of damping?

A

Light
Heavy
Critical

76
Q

Describe light damping of a system

A

The system oscillates over a long time frame before coming to rest.
The amplitude of the oscillations exponentially decay.

77
Q

What is the equation for linear velocity?

A
79
Q

In circular motion which direction do the acceleration and centripetal force vectors act?

A

Always towards the centre

80
Q

What is the condition for circular motion to happen?

A

A velocity needs to be acting perpendicular to a resultant force

83
Q

What is Fcentri for an object at the top of the vertical circle?

A
84
Q

What is Fcentri for an object on top of a vertical circle?

A
85
Q

What is Fcentri for an object at the bottom of a vertical circle?

A
86
Q

How do you find out the minimum velocity for an object travelling in a vertical circle?

A

Set R=0 (or tension if ball on string)

And rearrange for v

87
Q

How do you find out the maximum velocity for an object travelling over a vertical circle? (eg car over a hill)

A

Set reaction R=0

Then rearrange for v

88
Q

When solving angled circular motion problems what are the 3 usual steps?

A
  1. Set vertical component of force = weight
  2. Work out horizontal component using trig
  3. Fcentri = horizontal component
89
Q

Why can’t a ball be swung around in a circle with the string horizontal?

A

There must be a vertical component of the tension to match the weight

Otherwise ball is not in vertical equilibrium

90
Q

What are the two conditions for SHM?

A
  1. Acceleration must be proportional to displacement
  2. Acceleration must be opposite to displacement
91
Q

How does the time period differ for the two pendulums?

A

Time period is independent of amplitude

93
Q

Label up the maximum and minimum velocities and accelerations on the simple pendulum…

A
94
Q

Label up the maximum and minimum velocities and accelerations on the mass spring system…

A
95
Q

Label up the maximum and minimum potential and kinetic energies on the simple pendulum…

A
96
Q

What are the kinetic energy, potential energy and total energy lines for one cycle of SHM?

A
98
Q

How do you calculate KEmax or PEmax or ET in SHM?

A
99
Q

What two factors affect the time period of a mass spring system in SHM?

A
  1. Mass on the end of the spring
  2. Spring constant (stiffness) of spring
100
Q

What two factors affect the time period of a mass spring system in SHM?

A
  1. Length between top of string and centre of bob
  2. Gravitational field strength
101
Q

What does the graph of energy against displacement look like in SHM?

A
102
Q

How do you deal with rpm? (revolutions per minute)

A

÷60 to convert to rps (revolutions per second)

Then set rps = frequency

103
Q

When an SHM system is lightly damped what happens to its amplitude and time period?

A

Amplitude decreases (as it loses energy)

But time period remains constant

104
Q

How is natural frequency determined for a mass spring system?

A
105
Q

How is natural frequency determined for a simple pendulum?

A
106
Q

Define frequency

A

The number of complete oscillations per second

108
Q

Why is an object in circular motion accelerating?

A

Its linear velocity does not change in magnitude

But is constantly changing in direction

109
Q

The graph below shows driven oscillations with varying frequencies.

Add two lines if the system is:

  1. Undamped (free oscillations)
  2. Over damped
A
110
Q

For Barton’s pendulum which two balls oscillate?

A

P and Y because they have the same length

So natural frequency of y matches frequency of driving force from P

113
Q

What happens if…

Fcentri > Fmax

A

Circular motion does not happen

(Eg car skids off the road or moves to a higher radius)

114
Q

What happens if…

Fcentri max

A

Circular motion happens

(eg friction is large enough to keep car on track)

124
Q

Define amplitude.

A

The maximum displacement of an obejct/particle/point from equilibrium position

129
Q

When do you use?

x=Acos(wt)

When do you use?

x=Asin(wt)

A

x=Acos(wt) -> displacement in SHM when x=A when t=0

x=Asin(wt) -> displacement in SHM when x=0 when t=0

134
Q

Does circular motion count as SHM?

A

When projected onto a flat surface, yes it does

138
Q

What happens if the frequency of driving force is less than the natural frequency of a system?

f0

A

Low amplitude oscillations

With 0 phase difference.

139
Q

What happens if the frequency of driving force matches the natural frequency of a system?

f=f0

A

Resonance occurs

Large amplitude oscillations

π/2 radians out of phase

140
Q

What happens if the frequency of driving force is more than the natural frequency of a system?

f>f0

A

Low amplitude oscillations

With phase difference of π

Jen's B-Block (4 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions