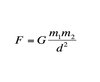Mechanics

Question 1

Velocity

Answer 1

v = ds/dt

Question 2

Acceleration

Answer 2

a = dv/dt

Question 3

General Motion Formulas (4)

v =

x =

v² =

v̅ =

Answer 3

v = v₀ + at

x = x₀ + v₀t + ½at²

v² = v₀2 + 2a(x − x₀)

v̅ = ½(v + v₀)

Question 4

Newtons 2nd Law (2 Forms)

“Sum of the forces…”

Answer 4

∑ F = m a

∑ F = dp/dt

(p = momentum)

Question 5

Weight

Answer 5

W = m g

Question 6

Centripetal Acceleration (2 Forms)

Answer 6

a_c = v²/r

a_c= − ω²r

Question 7

Momentum

Answer 7

p = m v

Question 8

Efficiency

Answer 8

ℰ = W_out /E_in

Question 9

Impulse

Answer 9

J = F̅ Δt

J =∫ F dt

Question 10

Impulse–Momentum

Answer 10

F̅ Δt = m Δv

∫F dt = Δp

Question 11

Work

Answer 11

• W* = F̅Δs cos θ
• W* = ∫F · ds

Question 12

Work–Energy

Answer 12

F̅Δs cos θ = ΔE

∫F · ds = ΔE

Question 13

Kinetic Energy (KE)

Answer 13

KE = ½mv²

Question 14

Potential Energy (PE) (U)

Answer 14

ΔU = − ∫F · ds

Question 15

Gravitational Potential Energy

Answer 15

ΔU_g = mgΔh

Question 16

Elastic Potential Energy

Answer 16

U_s= ½kΔx²

Question 17

Power

Answer 17

P̅ = F · v = F̅v cos θ

P̅ = ΔW / Δ*t = dW * / dt

Question 18

Angular Velocity

Answer 18

ω̅ = Δθ/Δt = dθ/dt

v = ω × r

Question 19

Angular Acceleration

Answer 19

α̅ = Δω/Δt = dω/dt

a = α × r − ω2 r

Question 20

General Rotation Formulas (4)

ω =

θ =

ω² =

ω̅ =

Answer 20

ω = ω₀ + αt

θ = θ₀ + ω₀t + ½αt²

ω²= ω₀2 + 2α(θ − θ₀)

ω̅ = ½(ω + ω₀)

Question 21

Newtons 2nd Law for Rotation (2 Forms)

“Sum of the torques…”

Answer 21

∑ τ = I α

∑ τ = dL/dt

(L = angular momentum)

Question 22

Torque

Answer 22

τ = rF sin θ

τ = r × F

Question 23

Moment of Inertia

Answer 23

I = ∑ mr²

I = ∫r² dm

Question 24

Parallel Axis Theorem

Answer 24

I = I_cm + mh²

(h = distance between center of mass and pivot point)

Question 25

Rotational Work

Answer 25

W = τ̅Δθ

W = ∫τ · dθ

Question 26

Rotational Power

Answer 26

P = τ · ω

P = τω cos θ

Question 27

Rotational Kinetic Energy

Answer 27

KE = ½Iω²

Question 28

Angular Momentum

Answer 28

L = r × p

L = mrv sin θ

L = I ω

Question 29

Frequency

Answer 29

ƒ = 1/T

ω = 2πƒ

Question 30

Hooke’s Law

Answer 30

F = − k Δx

Question 31

Universal Gravitation

Answer 31