Maths Flashcards
How do you find a limit of a simple function where the limit occurs as x→a?
Substitute in a+δ and evaluate the function, the limit will be where δ→0
How do you resolve limits of x→∞ for product and quotient functions?
For product, find the value that each part tends towards, then find which one will dominate.
For quotient, divide the whole fraction by the largest power of x, the 1/x values tend towards zero meaning the remaining values can be evaluated.
What is l’Hopital’s rule for limits?
The differential of a function will tend towards the same value as the function.
How do you differentiate from first principles?
lim(Δx→0) of (f(x+Δx)-f(x))/Δx
What is the derivative of tan(ax) and sec(ax)?
asec2(ax) and asec(ax)tan(ax) respectively
What is the product rule and the quotient rule for differentiation?
d/dx(uv)=uv’+u’v
d/dx(u/v)=(u’v-uv’)/v2
What are the two parts of the eigen operation?
The eigenfunction which repeats and the eigenvalue that changes
What is a point of inflection?
A point where the graph changes from concave to convex, it does not have to be a stationary point.
What is the difference between stationary and turning points?
Stationary points are points where f’(x)=0, turning points are where dy/dx changes sign on passing through the point.
What 3 situations can occur when f(2)(x)=0? How can these be futher evaluated?
For stationary inflection points, f(1)(x)=0 and f(3)(x)≠0
For not stationary inflection points, f(1)(x)≠0 and f(3)(x)≠0
For turning points, f(1)(x)=0, f(3)(x)=0 and f(4)(x)≠0
How can functions with multiple variables be differentiated?
Using partial derivitives, treating all but one variable as constant.
For f(x,y)=xy (δf/δx)y=δf/δx=fx=y
When does a function with two variables have a stationary point when x0=x and y0=y?
When the partial derivatives for each variable both equal zero:
fx(x0, y0)=fy(x0, y0)=0
For two variable systems, what is the formula for D and what can it determine?
D=fxx(x0, y0)fyy(x0, y0)-fxy(x0, y0)2
Local minimum when D>0 and fxx(x0, y0)>0
Local maximum when D>0 and fxx(x0, y0)<0
Saddle point when D<0
How can the differential of a function with two variables be found?
How can this be used?
By taking the partial derivatives of each variable and adding them together.
When finding the relative error of a measurement of these functions, dP/P.
What is the equation for integration by parts?
int(udv)=uv-int(vdu)
When integrating something containing (1-x2)½, what would be an appropriate subsitution?
x for cosu or similar as cos2u+sin2u=1
What are differential equations and how are simple ones solved?
Differential equations are where an equation contains a differential such as dy/dx and are solved by multiplying out the factors so an intergration can be done on both sides.
How do you solve first order linear differential equations?
The general form is dy/dx+yP(x)=Q(x)
The solution is y=R(x)-1•int(R(x)Q(x)dx) where R(x)=eint(P(x)dx)
How do you solve second order differential equations with constant coefficients where Q(x)=0?
The general form is d2y/dx2+c1dy/dx+c2y=0
This form suggests that it is a function that is multiplied by a constant when differentiated such as eax, as such we substitute this in for y.
d2eax/dx2+c1deax/dx+c2eax=0
a2eax+ac1eax+c2eax=0
2 roots can be found from a2+c1a+c2=0, a1 and a2.
General solution: y=Aea1x+Bea2x where A and B are constants based on the boundary conditions.
How is the sum of the first n terms in a finite series represented?
For the series: a+ax+ax2+…..+axn-1
Sn=a(1-xn/1-x)
What is the ratio test for convergance or divergance?
As r→∞, a series converges if |ur+1/ur|<1 and diverges if |ur+1/ur|>1 where ur and ur+1 are the rth and (r+1)th terms in the series
What is the Maclaurin series?
What is the Maclaurin series for y=ex?
An expansion of the generic function f(x) about the point x=0, a specific type of the Taylor series.
First find the 1 to nth derivatives for a function. Then resovle them for x=0. Then multiply the result by x to the power of the derivative number and divide by the derivative number factorial
so (f(n)(0)/n!)xn
y=ex=1+x+(x2/2!)+(x3/3!)+…+(xn/n!)+…
What is the general form of the Taylor series?
f(x)=f(a)+f(1)(a)(x-a)+(f(2)(a)/2!)(x-a)2+…+(f(n)(a)/n!)(x-a)n+…
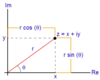
What is the general form for complex numbers?
z=x+iy
Where x is the real part of z, Re z, and y is the imaginary part of z, Im z.
What is the complex conjugate?
z*=x-iy
Where the imagianary part of the number is reversed in sign.
How do you divide complex numbers?
You multiply both sides of the fraction by the complex conjugate of the denominator. This gives a real denominator on the product.
Draw and label parts of an Argand diagram.
What is the argument and modulus of z?
The argument is θ and the modulus is r.
What is the polar form of complex numbers?
How can this be compressed?
z=r(cosθ+isinθ)
Using the Maclaurin series for cosθ and sinθ, the polar form can be rewritten as z=reiθ
What is Euler’s formula?
eiθ=cosθ+isinθ
What is the complex conjuate in polar form?
z=r(cosθ-isinθ)=re-iθ
What is the De Moivre theorem and where does it come from?
zn can be expressed as rneinθ
This can then be reintroduced to trig functions to find the De Moivre theorem:
(cosθ+isinθ)n=cosnθ+isinnθ
How do you find vector magnitudes and unit vectors?
Vector magnitudes are represented by |a|=(x2+y2+z2)½ where x, y and z refer to the i, j and k directions.
Unit vectors are â=a/|a|, these are vectors divided by their own magnitude.
What is the scalar product of two vectors and how can the angle between them be found?
a•b= the i, j and k parts of each vector multiplied by the same letter i, j and k parts.
The rule for the angles is a•b=|a||b|cosθ
What is the vector product of two vectors?
axb where you multiply each i, j and k part by the different i, j and k parts of the other vector. The triangle of i→j→k→i decides if the result is the positive or negative version of the other unit. e.g ixj=+k, kxj=-i, therefore axb≠bxa
