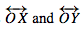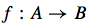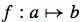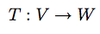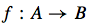Mathematics of Geometry, Mappings Flashcards
What is this set called?
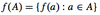
It is the range of f.
Give A and B in y = Ax + B if the equation represents a pure scaling.
B = 0. A is the matrix
q 0
0 p
Zero except on the diagonal.
What is a figure?
A figure is a set of points in Euclidean space, which corresponds to a set of vectors.
We can say each point P is an element of the figure.
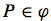
Name and define this.
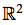
This is the two-dimensional vector space of real numbers.
It is the collection of all vectors describing all points in E2.
What is this?
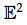
The Euclidean Plane.
What kind of transformation is this?
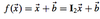
This is a translation, a type of affine transformation.
When is this mapping linear?
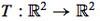
When the following equality holds.
Name two non-affine transformations.
Reflection and shear.
What is this?
This is the composition of f and g.
(g o f)(a) is g(f(a)) for any a in A.
If f maps A to B and g maps B to C then (g o f) maps A to C.
If the determinant of matrix A is zero, is A invertible?
A is not invertible if its determinant is zero.
Conversely, if A’s determinant is nonzero, it is invertible.
Is a projection transformation linear?
Yes, a projection transformation is linear but non-affine.
What do we know about the composition of two bijections?
The composition of two bijections is also a bijection.
If A is invertible, what kind of transformation is this?
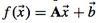
This is an affine transformation.
An affine transformation of the plan has an inverse which is also an affine transformation.
When is this surjective?
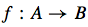
When f(A)=B
Which says that every element of B is the image of at least one element of A.
Also called onto
What is this?
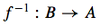
This mapping is the inverse of f if the following is true for every a in A.
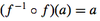
What do we know about the composition of affine transformations?
The composition of affine transformations is also an affine transformation.
How is this defined if sigma is a figure?
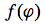
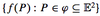
If x and y on the 2D coordinate plane are to be represented by homogeneous coordinates (a,b,w), name a translation that will represent infinity in 2D coordinates.
x=a/w
y=a/w
So the point (1,1,0) is one way to represent infinity
Homogeneous coordinates add a concept of infinity to Euclidean coordinates, which lack them.
When is this injective?
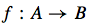
When each element in the range of f is the image of exactly one element in A.
When a set is injective, f(x)=f(y) implies x=y.
Define the rotation matrix in this rotation transformation.
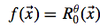
What are the terms for A and B in this?
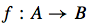
A is the domain of f. B is the codomain of f.
Name the properties of an affine transformation
(1) maps a line to a line,
(2) maps a line segment to a line segment,
(3) preserves the property of parallelism among lines and line segments, (4) maps an n-gon to an n-gon,
(5) maps a parallelogram to a parallelogram,
(6) preserves the ratio of lengths of two parallel segments, and
(7) preserves the ratio of areas of two figures.
What is a singular matrix?
A matrix that is not invertible.
What is the transformation of a set?
It is the bijection of a set unto itself.
Each transformation of the Euclidean Plane corresponds to a transformation of the 2D vector space of real numbers.
If f(P)=P’, then
f~() =
Both point and vector transformations are allowed.
How is a vector space generally defined?
A vector space is any collection of objects on which addition and multiplication are defined such that they have the following properties:
Addition must be a closure, associative and commutative laws are obeyed, and additive inverse and identity exist.
Multiplication must meet the following requirements with scalars: must be a closure, unitary, associative and both kinds of distributive laws must be obeyed
State the fundamental theorem of affine transformations
Given two ordered sets of three noncollinear points each, there exists an affine mapping f between those two sets.
And affine transformation between sets of points preserves collinearity and distance ratios.
Give A and B in y = Ax + B if the equation represents a pure rotation.
B = 0. A is the matrix
cos(θ) sin(-θ)
sin(θ) cos(θ)
What does OXY denote?
A coordinate system (not necessarily cartesian) with the following axes.
Give A and B in y = Ax + B if the equation represents a pure translation.
A is I, and B is the translation coordinates.
What is meant by this?
This is the function or mapping from A to B.
It consists of the set of ordered pairs (a,b) where a is an element of A and b is an element of B, with the following properties: For every a, there exists a unique b such that (a,b) is an element of the mapping f.
Another denotation: f(a)=b.
Still another denotation:
When is T a linear mapping?
When
T(u+v) = T(u) + T(v)
and
T(cu) = cT(u)
What are the terms for a and b in this?
b is the image of a in is f.
a is the preimage of b in f.
When is this bijective?
When it is both injective and surjective.
