Mathematics & Measurements

Question 1

Define:

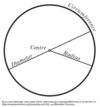
Circumference

Answer 1

Circumference is the perimeter of a circle.

The circumference of a circle can be calculated using radius or diameter: C = 2 * π * r or C = π * d

Question 2

How many sides does a pentagon have?

Answer 2

Five

Polygons are made using the Greek prefix for the number + the suffix “gon”. The other main polygons are:

• hexagon (6 sides)
• heptagon (7 sides)
• octagon (8 sides)
• nonagon (9 sides)
• decagon (10 sides)
• etc.

Question 3

Convert:

1 inch to centimeters

Answer 3

1 inch = 2.54 centimeters

Question 4

Which French philosopher and mathematician is famous for his creation of the Cartesian coordinate system, still used today in algebra and geometry?

Answer 4

René Descartes (1596-1650)

You may remember the Cartesian coordinate system as a plot of X, Y on a two-dimensional axis. This changed the way mathematicians were able to describe functions (correlational relationships).

Question 5

__________ data includes numerical measurements and __________ data includes descriptive words.

Answer 5

Quantitative (or empirical); qualitative

Question 6

How do you calculate percent change?

Answer 6

Percent change is calculated by dividing the difference between the two numbers by the original number, then multiplying by 100 to convert to percentage.

For example: A shirt was originally $4, but is now $6. What is the percent change?

Step 1: 6 - 4 = 2

Step 2: 2 / 4 = .5

Step 3: .5 * 100 = 50%

Question 7

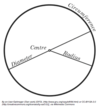
Define:

Diameter

Answer 7

Diameter is the distance from one side of a circle to the other measured in a straight line through the center.

Question 8

Define:

Volume

Answer 8

Volume is the amount of space within a three-dimensional figure. It is measured in units of distance cubed.

Common volume equations include:

• Sphere: (4/3) * π * r³
• Cylinder: V = (π * r * r) * h
• Square Pyramid: V = (l * w * h) / 3
• Rectangular Prism: V = l * w * h

Question 9

What is the Fibonacci Sequence?

Answer 9

The Fibonacci Sequence is a number sequence in which the next term is always the sum of the previous two.

0, 1, 1, 2, 3, 5, 8, 13, 21, etc.

The sequence is named after the Italian mathematician Fibonacci, though its origins actually come from early Indian mathematics.

Question 10

Define:

normal distribution

Answer 10

Bell-shaped, symmetric curve that represents data about many natural phenomena throughout the population

Question 11

What is the difference between Fahrenheit and Celsius?

Answer 11

Fahrenheit and Celsius are both units of measure for temperature. Fahrenheit is primarily used in the United States, whereas Celsius is part of the metric system and is used worldwide.

Converting Fahrenheit and Celsius can be achieved using some basic math:

°F = (°C × 9/5) + 32

°C = (°F − 32) x 5/9

Question 12

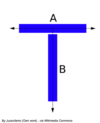
Define:

perpendicular

Answer 12

Lines that form a 90º angle at their intersection.

Question 13

What is an imaginary number and why are they important?

Answer 13

An imaginary number is any number that when squared, results in a negative number.

Imaginary numbers were once mocked and thought to be useless, but have since been applied to serious mathematics applications. One such example is in electronics, where imaginary numbers are used to calculate current.

Question 14

Define:

Acre

Answer 14

A measure of area; measures exactly 43,560 square feet.

Question 15

Define:

Area

Answer 15

Area is the measure of space on a surface. It is measured in units squared.

Common area equations include:

• Circle: A = π r^2
• Triangle: A = 1/2 b * h
• Rectangle: A = s1 * s2
• Parallelogram: A = b * h

Question 16

Define:

Factors

Answer 16

Factors are numbers that a number is evenly divisible by. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.

Question 17

Define:

Mean

Answer 17

The average of a group of numbers.

For example, the mean of 1, 2, 3, 4, 5 is 3.

Question 18

Define:

Median

Answer 18

The middle number in a set of numbers when they are ordered from least to greatest.

For example, the median of 1, 4, 2, 9, and 7 is 4.

Question 19

Define:

Mode

Answer 19

The most commonly occurring number in a set.

For example, the mode of 1, 1, 2, 2, 2, 6, 7, 7 is 2.

Question 20

Define:

Multiples

Answer 20

Multiples are numbers that result when you multiply a number.

For example, the multiples of 3 include 3, 6, 9, 12, etc.

Question 21

Define:

parallel

Answer 21

Lines that are the same distance apart at every point along their length and never touch are called parallel.

Question 22

What is pi?

Answer 22

In a circle, the ratio of its circumference to diameter is always pi.

Pi is usually rounded to 3.14, but is actually an infinite decimal that never repeats or ends. The first several digits are: 3.14159265358979

Question 23

What are the qualifications for a number to be considered prime?

Answer 23

A number is prime if it is divisible by only 1 and itself.

For example, 11 is prime, since its only factors are 1 and 11. The opposite of a prime number is called a composite number. 10 is not prime, and would therefore be categorized as composite, since its factors include 1, 2, 5, 10.

Exceptions:

• 0 is neither prime nor composite.
• 1 is neither prime nor composite. A common misconception is that 1 is prime, but it is not technically “divisible by 1 AND itself.”

Question 24

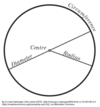
Define:

Radius

Answer 24

The distance from the center of a circle to its edge.

Question 25

Why do we use Roman numerals and how do you read them?

Answer 25

Roman numerals originated as a counting system in ancient Rome. These characters are still prevalent in architecture, but also in more modern-day applications (e.g. Super Bowl XLVIII).

The seven numerals used today:

• I - 1
• V - 5
• X - 10
• L - 50
• C - 100
• D - 500
• M - 1000

Roman numerals are written largest to smallest. If a smaller number is placed before a larger one, that value should be subtracted from the larger one. For example: IX is 9 (10-1).

Question 26

When measuring angles, how are degrees and radians different?

Answer 26

Degrees are mathematically abstract (not meaningful numbers), whereas radians have mathematical basis.

For example, a circle is arbitrarily divided into 360 degrees, but in radians is measured as as 2π. Radians are used in actual calculations. Degrees are typically used for more practical purposes such as navigation (e.g. the turn is 90 degrees to the left).

Question 27

What is statistical significance and why is it important?

Answer 27

• Statistical significance is used to determine if a result occurred by chance.
• Significance levels are used in research to decide whether an intervention produces a significant effect.
• When designing an experiment, it is important to collect data from enough subjects to achieve statistical power.

Question 28

What is a quick way of figuring out a tip (gratuity)?

Answer 28

Give two dollars for every ten. This results in a 20% tip.

For example, if the total bill is $61.00, tip $12.00.

Question 29

Which Greek mathematician, known as the “Father of Geometry,” wrote “Elements,” which continues to influence the study of geometry today?

Answer 29

Euclid (Lived around 300 B.C.)

Question 30

This philosopher and mathematician is most famous for this theorem in geometry that has a similar name to his own: a² + b² = c²

Answer 30

Pythagoras (570 BC – 495 BC)

The geometric theory is known as the Pythagorean Theorem, and is commonly used to deduce the missing side of a right triangle when the length of the other two sides are known.

Question 31

Convert:

1 gallon to liters

Answer 31

1 gallon = 3.785 liters

Question 32

Convert:

1 pound to kilograms

Answer 32

1 pound = 0.453 kilograms

Question 33

Convert:

1 pound to ounces

Answer 33

1 pound = 16 ounces

Question 34

Convert:

1 mile to kilometers

Answer 34

1 mile = 1.609 kilometers

Question 35

Convert:

1 yard to feet

Answer 35

1 yard = 3 feet