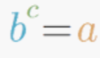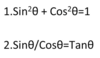Math Notes Flashcards
Pythagorean theorem not true for any triangle. Only applies to right triangles.
If a2 + b2 < c2, then the triangle would be an obtuse-angled triangle.
If a2 + b2 > c2, then the triangle would be an acute-angled triangle.
An expression is said to a perfect square trinomial if it takes the form ax^2 + bx + c and satisfies the condition
b^2 = 4ac
Factoring a Sum of Cubes:
Factoring a Difference of Cubes:
Factoring a Sum of Cubes:
a^3 + b^3 = (a + b)(a^2 – ab + b^2)
Factoring a Difference of Cubes:
a^3 – b^3 = (a – b)(a^2 + ab + b^2)
i imaginary number table
4 possible values
“AAS” is when we know two angles and one side (which is not between the angles).
“ASA” This means we are given two angles of a triangle and one side, which is the side adjacent to the two given angles.
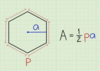
The quotient of each side measure divided by opposite angle’s sin is the same for all sides.
Use degrees seen from Radians when calculating sin or cos
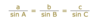
“SAS” This means we are given two sides and the included angle.
Cosine of the side you’re looking for
Use degrees seen from Radians when calculating sin or cos
Radian equal to
57.2958 degrees
180/3.141592
360/ 2PI
Only Right Triangles
“Hypotenuse” is the long one
“Opposite” is opposite to the angle θ (looking for)
“Adjacent” is adjacent (next to) to the angle θ
SOH CAH TOA
logarithm
a quantity representing the power to which a fixed number (the base) must be raised to produce a given number.
Sphere Volume
(4/3)*3.141592*r^3
Units of Length
Quadratic Formula
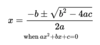
Common Logarithms
The common log of a number N is expressed as; log 10 N or log N. Common logarithms are also known as decadic logarithm and decimal logarithm
Formula to know number of solutions
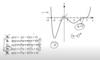
Sin Graph
Cos graph
Tan graph
“Pythagorean” trigonometric identities
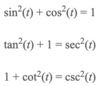
Basic Trigonometric Identities
Period of a function
A function f will be periodic with period m, so if we have
f (a + m) = f (a), For every m > 0
Period of Trig Functions
sin cos sec csc = 2PI/b
tan cot = PI/b
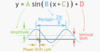
Expected value
In probability theory, the expected value of a random variable X, denoted E(X) or E[X], is a generalization of the weighted average, and is intuitively the arithmetic mean
Operations with matrixes
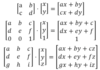
Multiplication and Determinant
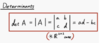
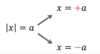
Two solutions, solving functions with absolutes
The Discriminant
We can only multiply matrices if the number of ___ in the ___ matrix is the ___ as the number of ___ in the ___ matrix.
We can only multiply matrices if the number of columns in the first matrix is the same as the number of rows in the second matrix.
How to multiply Matrices
Each on the first column attack each on the first row and take the place of the one in the columns
Multiplicity
(x−2)2=(x−2)(x−2)(x−2)2=(x−2)(x−2)
The factor is repeated, that is, the factor (x−2)(x−2) appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity. The zero associated with this factor, x=2x=2, has multiplicity 2 because the factor (x−2)(x−2) occurs twice.
Learning Outcome of Polynomials (graph)
Observe the behavior of the graph surrounding x-intercept. Three types of y=0: multiplicity 1 when the graph crosses as a straight line. Multiplicity of 2 when it bounces off. Multiplicity of 3 when it curves up and down.
To find shaded-type graph for equations such as ax + by < c
(3 steps)
1- Give simple values to a, b, c. (1, 2, 3)
2- Find x and y-intercepts
3- Determine the shadowed side by testing the origin
gives the x-coordinate of the vertex of a quadratic equation (parabola) in the form
y=ax2 + bx + c
-b/2a
maximum or minimum x coordinate
Reword logarithm base b of a equals c
___ to the ___ power equals ___
logarithm base b of a equals c
=
b to the c power equals a
Median
Arrange your numbers in numerical order.
Count how many numbers you have.
If you have an odd number, divide by 2 and round up to get the position of the median number.
If you have an even number, divide by 2. Go to the number in that position and average it with the number in the next higher position to get the median.
Parallelogram + area formula
a four-sided plane rectilinear figure with opposite sides parallel.
area formula is bh for any parallelogram
Slope of vertical line and horizontal line
slope of vertical line is undefined
slope of horizontal line is 0
Exponents rules and properties
(product, quotient and power)
Each trigonometric function in terms of each other
sine of an angle is equal to the cosine of the other angle (in a right triangle) so sinx = cos(90-x)
Complex numbers’ cardinal plane. How to measure distance?
Real numbers are on the x-axis, imaginary numbers are treated as units on the y-axis
Reciprocal
a mathematical expression or function so related to another that their product is one; the quantity obtained by dividing the number one by a given quantity.
Secant
the ratio of the hypotenuse to the shorter side adjacent to an acute angle (in a right-angled triangle); the reciprocal of a cosine.
Cosine = Adjecent / Hypotenuse
Secant = Hypotenuse / Adjacent
sin cos tan csc sec cot
sin o/h
cos a/h
tan o/a
csc h/o
sec h/a
cot a/o
Special triangle
3 / 4 / 5
A triangle with sides of 3, 4, and 5 will always be a right
triangle, even if the problem does not explicitly state it.
Special triangle
45o/45o/90o
In these triangles, the ratio of sides will always be 1:1:sqt(2)
Special triangle
30o/60o/90o
1 : 2 : sqt(3)
When two triangles have the same angles
they share the ratios of their sites
To get the slope ? remember that…
Delta Y divided by Delta X. Remember: result might be a negative number
Vertex for parabola (2 methods)
Calculator instructions for cot
90 minus degrees divided by 57.3 then tan
The circumradius
The circumradius of a cyclic polygon is the radius of the circumscribed circle of that polygon. For a triangle, it is the measure of the radius of the circle that circumscribes the triangle. Since every triangle is cyclic, every triangle has a circumscribed circle, or a circumcircle.
Formula for apothem
Formula for regular polygon
Value of theta and Pi during trigonometric operations
(theta being the degrees the operations apply to)
Pi = 180 degrees
Theta = degrees / radian
Solutions for inequality
Solve inside parenthesis using same symbol
Once you get the two factors of the polynomial in the form (x+a)(x+b)
Don’t forget to invert the sign for the answer
The formula for a circle is (x - a)2 + (y - b)2 = r2, where (?, ?) is the center of the circle and ? is the radius of the circle.
where (a, b) is the center of the circle and r is the radius of the circle.
Period, value at zero, initial slope and range all trig graphs
Gallons Mililiters convertion chain
Gallon = 4 Quarts / Quart = 2 Pints / Pint = 2 cups / Cup = 8 oz
oz = 29.57 mL
32 ounces in a quart
In triangle problems, angle A is opposite of side
a
To test calculator sin of 90 should be
1
Kite
A quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other.
Area= product of the lengths of the diagonals divided by 2 = Dd/2
Trapezoid
Any cuadrilatreral with only one pair of parallel angles
area = ((B+b)xh)/2
Parallelogram
A = bh
Cuadrilateral with all opposite sides parallel to each other = rectangle, square, rhombus
Look again at what was being asked
after you’re done with your long calculations
log base 5 x = -2 what is x?
1/25
Arithmetic Sequence
if S1 = 3
S2 = 9
S3 = 22
S4 = 49
In sum of consecutive numbers the one in the middle (median) is
the mean
matrices are described as axb where a are the ? and b are the ?
number of ? in the first matrix has to be equal to the number of ? in the seconc matrix for a multiplication to be possible
The resulting size is ?x?
a is the height or number of rows and b is the number of columns or width
number of columns in the first one has to be equal to the number of rows in the second one
The rows of the first one by the columns of the second one
inner numbers qual, outer number result
Matrices: describe operation
Rows vs columns
First matrix attacks in rows, second matrix in columns. From first matrix, each item in the row pairs against each item in second matrix’s column. Products are summed resulting value is placed based on participating row/column
In a circle in the standard (x,y) coordionate plane, if an end of a diameter if z units above the center…
regardless of its x coordinate, the other end will also be z units from the center
Synthetic Division
(need a confirmed factor)
Ellipse Equation
squared y coordinate paired with squared x plus squared x coordinate paired with squared y equals the product of their x and y coordinate
Multiply by conjugate
first term as is second term negative use for fractions with i
