Math Flashcards
ab + ac
a(b + c)
a2 + 2ab + b
(a+b)2
a2 - 2ab + b2
(a - b)2
a2 - b2
(a - b)(a + b)
Area of triangle
Area = 1/2 (base)(height)
Isoscelese Triangle
Two equal sides with two equal angles
Special Right Triangles
3: 4:5
5: 12:13
30, 60, 90
1: rt3:2
1. here, the shortest side is half the hypotenuse
45, 45, 90
- sides are always 1:1:sqr2
Circumference of Circle
Area = 2πr
Area = πd
Area of Circle
Area = πr2
Original Whole; before percent increase/decrease
Decrease:
(1 - .x) x (original) = given
Increase:
ex: 15% increase over x = 1.15x
Simple Interest
interest = (principal) x (int rate) x (time)
Compound Interest
final = (principal) x (1 + Int rate / C) ^(time)(C)
C = num of times compounded
Remainder
Ex: remainder of 12 ÷ 7 is 5
Weighted Average
(Weight 1)(X1) + (W2)(X2)
divided by
(Weight 1) + (weight 2)
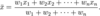
Combined Work
Combined Ratio
multiply one or both ratios until the term they have in common is the same. Then combine and remove the like term.
Dilution or Mixing
(percent dif b/w weaker and desired) x (amount of weaker) = (percent diff b/w stronger and desired) x (amound of stronger)
Group problem involving both or neither
group 1 + group 2 + neither - both = Total
Of the 120 students, 65 study french, 51 spanish, and 53 neither. How many study both french and spanish?
65 + 51 + 53 - both = 120
169 - both = 120
both = 49
Standard Deviation
- Find the average of the set
- Find Diff b/w mean and each value in set
- Square each of the diff
- Find the avg of the squared differences
- Take the positive square root of the averages
Multiplying values with exponents
(xa)(xb) = xa+b
23 x 24 = 27
Dividing Values With Exponents
like multiplying but substract exponents
56/ 52 = 54
Add Roots
Combine like roots only
ex: sq2 plus 3*sq2 = 4*sq2
Sequence
What is the diff b/w the fifth and fourth terms in the sequence 0, 4, 18, … whose nth term is n2(n-1)?
n5 = 52(5-1) = 25(4) = 100
n4 = 42(4-1) = 16(3) = 48
So, the difference b/w 4th and 5th terms is;
100 - 48 = 52
Max and Min lengths for a side of a triangle
Range is somewhere between the difference and the sum of the known lengths.
eg: given a triangle with sides 7 and 3
the third side is greater than the difference and less than the sum.
7-3 = 4
7 + 3 = 10
4 < x < 10
One angle or the sum of all angles of a Regular Polygon
((n - 2) x 180) / n
n = number of sides
ex: pentagon; n= 5
Arc Length
(n/360) x 2πr
Area of a sector
(n/360) x πr2
Volume of cylinder
V = (area of base) x height
V = πr2h
Cylinder Surface Area
2πr2 + 2πrh
Permutation
(The number of ways to arrange elements sequentially)
n! / (n-k)!
n = # in larger group
k = # you are arranging
ex: There are 5 runners, only 3 can place. How many possible outcomes?
n = 5; k = 3
Answer: 60
Combination
(if the order or arrangement of the smaller group does not matter)
n! / (k!(n-k)!)
n = # in larger group
k = num you are choosing
e: how many diff ways can you choose 3 delegate from 8 candidates?
n = 8; k = 3
Exponent raised to an exponent
(xa)b = xab
(34)5 = 320
Fractional Powers
(x-2)1/2 = x(-2)(1/2) = x-1 = 1/x
