Linked List Strategies

Question 1

Reverse a Singly Linked List

Given the pointer/reference to the head of a singly linked list, reverse it and return the pointer/reference to the head of reversed linked list.

Answer 1

Linear Runtime, Constant Memory

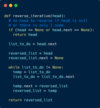
If the linked list only contains 0 or 1 nodes, then the current list can be returned as it is. If there are two or more nodes, then the iterative solution starts with 2 pointers.

1. reversed: A pointer to already reversed linked list (initialized to head).
2. list_to_do: A pointer to the remaining list (initialized to head->next).

We then set the reversed->next to NULL. This becomes the last node in the reversed linked list. reversed will always point to the head of the newly reversed linked list.

At each iteration, the list_to_do pointer moves forward (until it reaches NULL). The current node becomes the head of the new reversed linked list and starts pointing to the previous head of the reversed linked list.

The loop terminates when list_to_do becomes NULL and the reversed pointer is pointing to the new head at the termination of the loop.

Question 2

Remove Duplicates from a Linked List

We are given a linked list of integers and we have to remove all the duplicate nodes from it by keeping only the first occurrence of each duplicate.

Answer 2

Linear Runtime, Linear Memory

Here is the pseudo-code of the algorithm that we are going to use. We iterate through the entire linked list and compare each node data with the Hashset. Duplicate nodes are deleted as we iterate the list.

• n = length of linked list
• add data of first node to a hashset
• for 2nd to nth node in linked list
  
  • if data of ‘node’ is found is hashset: delete current node
  • else: add data of current node to hashset

Question 3

Delete Node with a Given Key

We are given the head of a linked list and a key. We have to delete the node that contains this given key.

Answer 3

Linear runtime, constant memory.

First, we have to find the key in the linked list. We’ll keep two pointers, current and previous, as we iterate the linked list. If the key is found in the linked list, then the current pointer would be pointing to the node containing the key to be deleted. The previous should be pointing to the node before the key node. This can be done in a linear scan and we can simply update current and previous pointers as we iterate through the linked list.

Question 4

Insertion Sort of a Linked List

Given the head pointer of a linked list, sort the linked list in ascending order using insertion sort. Return the new head pointer of the sorted linked list.

If the given linked list is 29 -> 23 -> 82 -> 11, then the sorted list should be 11 -> 23 -> 29 -> 82.

Answer 4

Polynomial, O(n²) runtime, Constant Memory Complexity

The concept of Insertion Sort is very simple. We’ll maintain two linked lists:

1. Original list (given to us as input).
2. Sorted list (initially empty).

Here is how the algorithm works.

• While the original list is not empty:
  
  • Remove an element (say ‘X’) from the original list.
  • Insert ‘X’ at the correct sorted position in the sorted list.

Question 5

Intersection Point of Two Lists

Given the head nodes of two linked lists that may or may not intersect, find out if they do in fact intersect and return the point of intersection. Return null otherwise.

Answer 5

Linear, O(m + n) runtime, Constant Memory. Here is the complete algorithm:

• Find lengths of both linked lists: L1 and L2
• Calculate difference in length of both linked lists: d = |L1 - L2|
• Move head pointer of longer list ‘d’ steps forward
• Now traverse both lists, comparing nodes until we find a match or reach the end of lists

Question 6

Nth from Last Node

Given a singly linked list, return the nth node from last. Return null if ‘n’ is out-of-bounds.

Answer 6

Linear Runtime, Constant memory

We will use two pointers to find the nth from the last node. The idea is to have two pointers n nodes apart: one pointing to the head, and the other pointing to the nth node. Then, we move both pointers forward until the second pointer reaches the tail. Now, the first pointer will be pointing to the nth node from last. If we reach the tail before making both pointers n nodes apart, that means n is out of bounds.

Question 7

Swap Nth Node with Head

Given the head of a singly linked list and ‘N’, swap the head with the Nth node. Return the head of the new linked list.

Answer 7

Linear Runtime, Constant Memory

We don’t want to just swap the values as that is inefficient for custom types. To swap the Nth node with the head, let’s find the (N-1)th node as we need node ‘(N-1)->next’ to become the new head. We will iterate the list until current points to the Nth node. ‘prev’ follows current and will be pointing to (N-1)th node. We’ll return current as the new head of the linked list.

Question 8

Merge Two Sorted Linked Lists

Given two sorted linked lists, merge them so that the resulting linked list is also sorted.

Answer 8

Linear O(m + n) runtime, where m and n are lengths of both linked lists. Constant Memory.

We maintain a head and a tail pointer on the merged linked list. We choose the head of the merged linked list by comparing the first node of both linked lists. For all subsequent nodes in both lists, we choose the smaller current node and link it to the tail of the merged list, and moving the current pointer of that list one step forward.

We keep doing this while there are some remaining elements in both the lists. If there are still some elements in only one of the lists, we link this remaining list to the tail of the merged list.

Question 9

Merge Sort

Given the head pointer of a linked sort, sort the linked list in ascending order using merge sort, and return the new head pointer of sorted linked list.

Merge sort is one of the standard sorting algorithms for a Linked List. If the given linked list is 29 -> 23 -> 82 -> 11, then the sorted (in ascending order) list should be 11 -> 23 -> 29 -> 82.

Answer 9

Linearithmic i.e. O(n * log n) runtime, Logarithmic O(log n) memory

The concept of merge sort is very straightforward. In the dividing step, we split our input linked list into two halves and keep doing so until there is a linked list of size 1 or 0. Linked lists of size 1 and 0 are always sorted. In the combining step, we merge sorted lists and keep doing so until we have a completely sorted list. The recurrence relation for this merge sort algorithm will be:

T(n)=2T(n/2)+n

At each step, we divide our problem into two sub-problems. The size of each sub-problem is n/2 and the total cost of combining step (merging sorted lists) is n.

If we solve this recurrence relation, the result will be O(n * log n) which is the time complexity of merge sort.

Question 10

Reverse Even Nodes

Given a singly linked list, reverse the nodes at even indices (starting at 1).

Answer 10

Linear Runtime, Constant Memory

We don’t want to copy the data of elements or re-allocate memory for nodes, as that is inefficient. We will create two lists comprising of nodes at even and odd indices. While extracting even nodes, we will push them to the head of list_even since we need them in reverse order while merging. Now that the two lists are in the correct order, it’s just a matter of merging their nodes alternately.

Question 11

Rotate a Linked List

Given the head node of a singly linked list and an integer ‘n’, rotate the linked list by ‘n’.

Answer 11

Linear runtime, Constant memory

Rotating by one node is very simple; just find the last node of linked list and move it to the head of the linked list. One way of solving our original problem is to rotate by one node (i.e. last node of linked list) n times. Getting to the last node of a linked list requires a linear scan, so this algorithm requires n scans of the linked list. The time complexity of this algorithm will be O(mn) where m is the length of the linked list and n is the number of rotations needed. However, there is an alternate and simpler algorithm which avoids multiple scans of the linked list. We know that performing n rotations (if n > 0) of the last node is equivalent to performing one rotation of the last n nodes of the linked list. So O(n) algorithm to find the list rotated by n nodes is below:

• Find the length of the linked list.
• If n is negative or n is larger than the length of the linked list, adjust this for the number of rotations needed at the tail of the linked list. The adjusted number is always an integer N where 0 <= N < n.
• If the adjusted number of rotations is 0, then just return the head pointer. This means that no rotations were needed.
• Find the nth node from the last node of the linked list. As we already have the length of the linked list, it is simpler. It is basically getting to the node ‘x’ at length ‘n - N’. Next pointer of node previous to this node i.e. ‘x’ should be updated to point to NULL.
• Start from ‘x’ and move to the last node of the linked list. Update next pointer of the last node to point to the head node.
• Make ‘x’ as the new head node. ‘x’ is now the head of the linked list after performing n rotations.

Question 12

Reverse k Elements

Given a singly linked list and an integer ‘k’, reverse every ‘k’ element. If k <= 1, then the input list is unchanged. If k >= n (n is the length of the linked list), then reverse the whole linked list.

Answer 12

Linear Runtime, constant memory

Algorithmically, it is a simple problem, but writing code for this is a bit trickier as it involves keeping track of a few pointers. Logically, we break down the list to sub-lists each of size ‘k’. We’ll use the below pointers:

1. reversed: it points to the head of the output list.
2. current_head: head of the sub-list of size ‘k’ currently being worked upon.
3. current_tail: tail of the sub-list of size ‘k’ currently being worked upon.
4. prev_tail: tail of the already processed linked list (where sub-lists of size ‘k’ have been reversed).

We’ll work upon one sub-list of size ‘k’ at a time. Once that sub-list is reversed, we have its head and tail in current_head and current_tail respectively. If it was the first sub-list of size ‘k’, its head (i.e. current_head) is the head (i.e. reversed) of the output linked list. We’ll point ‘reversed’ to current_head of the first sub-list. If it is the 2nd or higher sub-list, we’ll connect the tail of the previous sub-list to head of the current sub-list i.e. update next pointer of the tail of the previous sub-list with the head pointer of current sub-list to join the two sub-lists.

Question 13

Add Two Integers

Given the head pointers of two linked lists where each linked list represents an integer number (each node is a digit), add them and return the resulting linked list.

Answer 13

Linear runtime, Linear complexity

The integers are stored inverted in the linked lists to make the addition easier. Now, the most significant digit of the number is the last element of the linked list. For the addition, we’ll start from the heads of the two linked lists. At each iteration, we add the current digits of the two lists and insert a new node with the resulting digit at the tail of the result linked list. We’ll also need to maintain carry at each step. We’ll keep doing this for all digits in both the linked lists. If one of the linked lists ends sooner, we’ll continue with the other linked list. Once both of the linked lists are exhausted, and no carry is left to be added, the algorithm will terminate. Now, let’s walk through the solution step by step using this animation.

Question 14

Copy Linked List with Arbitrary Pointer

We are given a linked list where the node has two pointers. The first is the regular ‘next’ pointer. The second pointer is called ‘arbitrary_pointer’ and it can point to any node in the linked list. Your job is to write code to make a deep copy of the given linked list. Here, deep copy means that any operations on the original list (inserting, modifying and removing) should not affect the copied list.

Here’s an example of a linked list with arbitrary pointers connected.

Answer 14

Linear Memory, Linear Runtime

We will create a deep copy of the linked list in three passes.

1. Create a copy of each node so that the original node’s next pointer is pointing to its copy.
2. Fix the arbitrary pointers in the copied nodes.
3. Separate the copied linked list from the original linked list.